Bài 2.48 trang 58 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả.
Một chiếc gậy có chiều dài 2,5 m được đặt trong góc phòng như hình sau đây. Một đầu của chiếc gậy nằm trên sàn nhà, cách hai bức tường lần lượt là 1 m và 0,8 m. Đầu còn lại của chiếc gậy nằm trên mép tường.
Đề bài
Một chiếc gậy có chiều dài 2,5 m được đặt trong góc phòng như hình sau đây. Một đầu của chiếc gậy nằm trên sàn nhà, cách hai bức tường lần lượt là 1 m và 0,8 m. Đầu còn lại của chiếc gậy nằm trên mép tường.
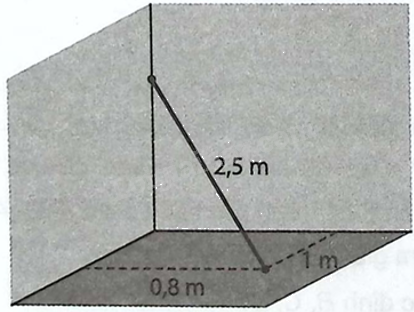
a) Hãy lập một hệ tọa độ \(Oxyz\) phù hợp và tìm tọa độ của đầu gậy nằm trên sàn nhà.
b) Tính khoảng cách từ đầu gậy trên mép tường đến sàn nhà.
Phương pháp giải - Xem chi tiết
Ý a: Lập hệ trục tọa độ dựa trên các yếu tố vuông góc.
Ý b: Gọi tọa độ điểm trên mép tường theo một tham số, tìm tham số đó và tìm khoảng cách.
Lời giải chi tiết
a) Ta lập hệ trục tọa độ như hình vẽ sau:
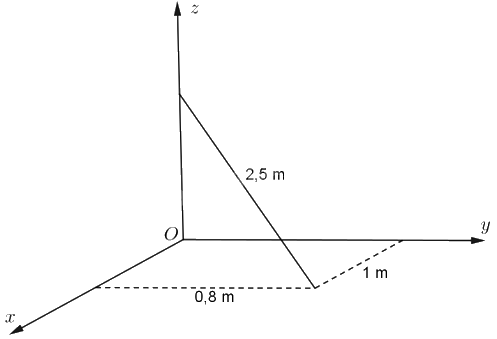
Suy ra đầu gậy trên sàn nhà có tọa độ là \(\left( {1;0,8;0} \right)\).
b) Ta thấy đầu gậy trên mép tường là một điểm thuộc tia \(Oz\) nên ta có thể sử điểm đó có tọa là \(\left( {0;0;a} \right)\) với \(a > 0\) đồng thời cũng có \(a\) chính là khoảng cách từ đầu gậy trên mép tường đến sàn nhà.
Mặt khác chiếc gậy có chiều dài 2,5 m, do đó ta có
\(\sqrt {1 + {{0,8}^2} + {a^2}} = 2,5 \Leftrightarrow \sqrt {{a^2} + 1,64} = 2,5 \Leftrightarrow a = \frac{{\sqrt {461} }}{{10}} \approx 2,15\).
Vậy khoảng cách từ đầu gậy trên mép tường đến sàn nhà \(2,15\) m.
Bài 2.48 trang 58 sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là đề bài chi tiết:
(Đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm đạo hàm f'(x) và xác định các điểm cực trị của hàm số.)
Để giải bài tập này, chúng ta thực hiện các bước sau:
Sử dụng quy tắc tính đạo hàm của hàm đa thức, ta có:
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Ta xét dấu của f'(x) trên các khoảng:
Vậy, hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2.
Hàm số y = f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị cực đại là f(0) = 2 và đạt cực tiểu tại x = 2 với giá trị cực tiểu là f(2) = -2.
Để hiểu sâu hơn về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế, học sinh có thể tham khảo thêm các tài liệu sau:
Việc luyện tập thường xuyên các bài tập về đạo hàm sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả. Chúc các em học tốt!
Để giúp các em hiểu rõ hơn, chúng ta cùng xét một ví dụ khác:
(Ví dụ khác về bài tập đạo hàm sẽ được chèn vào đây)
Giải bài tập này tương tự như bài tập trên, các em cần áp dụng các quy tắc tính đạo hàm và phân tích dấu của đạo hàm để tìm ra các điểm cực trị của hàm số.
Khi giải các bài tập về đạo hàm, các em cần chú ý:
Hy vọng với hướng dẫn chi tiết này, các em sẽ giải quyết thành công bài 2.48 trang 58 sách bài tập Toán 12 - Kết nối tri thức và các bài tập tương tự.