Giải bài 2.15 trang 46 Sách bài tập Toán 12 - Kết nối tri thức

Giải bài 2.15 trang 46 sách bài tập toán 12 - Kết nối tri thức

Giải bài 2.15 trang 46 Sách bài tập Toán 12 - Kết nối tri thức

Bài 2.15 trang 46 sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.15 trang 46, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho hình chóp S.ABC có \(SA = SB = SC\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Chứng minh rằng \(\overrightarrow {SA} \cdot \overrightarrow {BC} = \overrightarrow {SB} \cdot \overrightarrow {AC} = \overrightarrow {SC} \cdot \overrightarrow {AB} \).

Đề bài

Cho hình chóp S.ABC có \(SA = SB = SC\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\).

Chứng minh rằng \(\overrightarrow {SA} \cdot \overrightarrow {BC} = \overrightarrow {SB} \cdot \overrightarrow {AC} = \overrightarrow {SC} \cdot \overrightarrow {AB} \).

Phương pháp giải - Xem chi tiết Giải bài 2.15 trang 46 sách bài tập toán 12 - Kết nối tri thức 1

Sử dụng định lý ba đường vuông góc để tìm hình chiếu của \(S\) trên \(\left( {ABC} \right)\), tiếp tục dùng định lý này để chứng minh \(SA \bot BC\), \(SB \bot AC\) và \(SC \bot AB\). Từ đó suy ra các tích vô hướng của từng cặp vuông góc đều bằng 0, do đó chúng bằng nhau.

Lời giải chi tiết

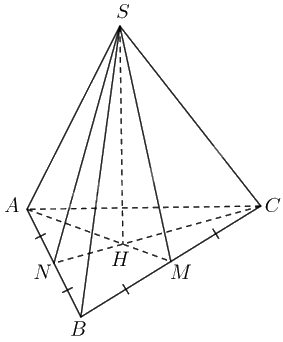
Giải bài 2.15 trang 46 sách bài tập toán 12 - Kết nối tri thức 2

Theo đề bài ta có ba tam giác \(SAB,{\rm{ }}SAC,{\rm{ }}SAB\) đôi một bằng nhau theo trường hợp cạnh-góc-cạnh. Do đó \(AB = BC = AC\) (cạnh tương ứng), suy ra tam giác \(ABC\)là tam giác đều.

Giả sử \(H\) là hình chiếu của \(S\) trên \(\left( {ABC} \right)\), kẻ \(HM \bot BC\) với \(M \in BC\) ta có \(SM \bot BC\).

Mặt khác, tam giác \(SBC\) cân tại \(S\)(giả thiết \(SB = SC\)) suy ra \(M\) là trung điểm cạnh \(BC\).

Từ đó suy ra \(HM\) là một phần đường trung tuyến của tam giác \(ABC\).

Tương tự, kẻ \(HN \bot AB\) ta thu được \(HN\) là một phần đường trung tuyến của tam giác

\(ABC\). Do đó ta có \(H\) là trọng tâm tam giác \(ABC\).

Ta có \(AM\) là hình chiếu của \(SA\) trên \(\left( {ABC} \right)\) và \(AM \bot BC\) suy ra \(SA \bot BC\) do đó \(\overrightarrow {SA} \cdot \overrightarrow {BC} = 0\)

Chứng minh tương tự ta thu được \(SB \bot AC\) và \(SC \bot AB\).

Vậy \(\overrightarrow {SA} \cdot \overrightarrow {BC} = \overrightarrow {SB} \cdot \overrightarrow {AC} = \overrightarrow {SC} \cdot \overrightarrow {AB} = 0\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài 2.15 trang 46 sách bài tập toán 12 - Kết nối tri thức đặc sắc thuộc chuyên mục đề thi toán 12 trên nền tảng đề thi toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài 2.15 trang 46 Sách bài tập Toán 12 - Kết nối tri thức: Tổng quan

Bài 2.15 trang 46 sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định tính đơn điệu của hàm số, và tìm cực trị của hàm số. Việc nắm vững kiến thức về đạo hàm là rất quan trọng để giải quyết bài toán này.

Nội dung bài 2.15 trang 46

Bài 2.15 thường bao gồm một hoặc nhiều câu hỏi nhỏ, yêu cầu học sinh thực hiện các bước sau:

Tính đạo hàm của hàm số đã cho.
Tìm tập xác định của hàm số.
Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị.
Xét dấu đạo hàm trên các khoảng xác định để xác định tính đơn điệu của hàm số.
Kết luận về cực đại, cực tiểu của hàm số.

Phương pháp giải bài 2.15 trang 46

Để giải bài 2.15 trang 46 hiệu quả, học sinh cần nắm vững các kiến thức sau:

Các công thức tính đạo hàm cơ bản (đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit).
Các quy tắc tính đạo hàm (quy tắc cộng, trừ, nhân, chia, đạo hàm hợp).
Cách xét dấu đạo hàm để xác định tính đơn điệu của hàm số.
Cách tìm cực trị của hàm số.

Ví dụ minh họa giải bài 2.15 trang 46

Giả sử bài 2.15 yêu cầu tìm cực trị của hàm số y = x³ - 3x² + 2.

Tính đạo hàm: y' = 3x² - 6x
Giải phương trình y' = 0: 3x² - 6x = 0 => x = 0 hoặc x = 2
Xét dấu đạo hàm:
- Với x < 0: y' > 0 => Hàm số đồng biến
- Với 0 < x < 2: y' < 0 => Hàm số nghịch biến
- Với x > 2: y' > 0 => Hàm số đồng biến
Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Lưu ý khi giải bài 2.15 trang 46

Khi giải bài 2.15 trang 46, học sinh cần lưu ý những điều sau:

Đảm bảo tính chính xác trong quá trình tính đạo hàm.
Kiểm tra kỹ tập xác định của hàm số.
Xét dấu đạo hàm một cách cẩn thận để xác định đúng tính đơn điệu của hàm số.
Kết luận về cực trị của hàm số một cách chính xác.

Bài tập tương tự và luyện tập

Để củng cố kiến thức và kỹ năng giải bài 2.15 trang 46, học sinh nên làm thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.

Giaitoan.edu.vn - Hỗ trợ học Toán 12 hiệu quả

Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong sách giáo khoa và sách bài tập Toán 12 - Kết nối tri thức. Chúng tôi hy vọng rằng với sự hỗ trợ của Giaitoan.edu.vn, các em học sinh sẽ học Toán 12 hiệu quả hơn và đạt kết quả tốt trong các kỳ thi.