Bài 1.12 trang 14 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.12 trang 14 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = 3{x^4} - 4{x^3}); b) (y = frac{{{x^2}}}{{x - 1}},x > 1).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = 3{x^4} - 4{x^3}\);
b) \(y = \frac{{{x^2}}}{{x - 1}},x > 1\).
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số. Từ bảng biến thiên ta tìm được giá trị lớn nhất, nhỏ nhất.
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = 12{x^3} - 12{x^2}\). Khi đó \(y' = 0 \Leftrightarrow 12{x^3} - 12{x^2} = 0 \Leftrightarrow 12{x^2}\left( {x - 1} \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
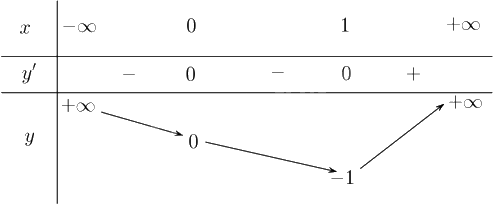
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} y = y\left( 1 \right) = - 1\); Hàm số không có giá trị lớn nhất.
b) Tập xác định: \(\left( {1; + \infty } \right)\)
Ta có \(y' = \frac{{2x\left( {x - 1} \right) - {x^2} \cdot 1}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\). Khi đó \(y' = 0 \Leftrightarrow \frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x = 2\) (vì \(x > 1\))
Lập bảng biến thiên của hàm số:
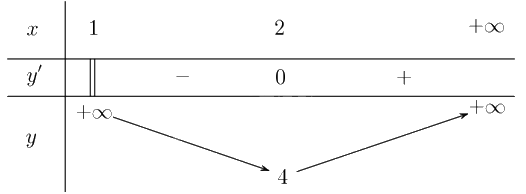
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( 2 \right) = 4\). Hàm số không có giá trị lớn nhất trên khoảng \(\left( {1; + \infty } \right)\).
Bài 1.12 trang 14 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Bài tập 1.12 yêu cầu tính giới hạn của hàm số tại một điểm cho trước. Cụ thể, bài tập có thể yêu cầu tính giới hạn của hàm số khi x tiến tới một giá trị cụ thể, hoặc khi x tiến tới vô cùng.
Để giải bài tập 1.12 trang 14, học sinh có thể áp dụng các phương pháp sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập 1.12 trang 14, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Ví dụ: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học, đặc biệt là trong giải tích. Nó được sử dụng để định nghĩa đạo hàm, tích phân, và các khái niệm quan trọng khác. Việc nắm vững kiến thức về giới hạn là nền tảng để học tốt các môn học cao cấp hơn.
Giaitoan.edu.vn là website học Toán online uy tín, cung cấp đầy đủ các bài giải, đáp án, và tài liệu học tập Toán 12. Chúng tôi luôn cập nhật những kiến thức mới nhất và phương pháp giải bài tập hiệu quả nhất để giúp các em học sinh đạt kết quả tốt nhất trong môn Toán.
Hãy truy cập Giaitoan.edu.vn để khám phá thêm nhiều bài giải Toán 12 và các tài liệu học tập hữu ích khác!