Bài 1.44 trang 31 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.44 trang 31 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng (3) km, một thị trấn ở điểm A cách điểm P (12) km (xem hình vẽ). Nếu một người trên đảo chèo thuyền với vận tốc (2,5) km/h và đi bộ với vận tốc (4) km/h thì thuyền nên neo đậu ở vị trí nào trên đoạn PA để người đó đến thị trấn trong thời gian ngắn nhất?
Đề bài
Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng \(3\) km, một thị trấn ở điểm A cách điểm P \(12\) km (xem hình vẽ). Nếu một người trên đảo chèo thuyền với vận tốc \(2,5\) km/h và đi bộ với vận tốc \(4\) km/h thì thuyền nên neo đậu ở vị trí nào trên đoạn PA để người đó đến thị trấn trong thời gian ngắn nhất?

Phương pháp giải - Xem chi tiết
+ Đặt ẩn và điều kiện cho ẩn biểu diễn khoảng cách từ A đến vị trí thuyền neo đậu trên đoạn PA.
+ Biểu diễn tổng quãng đường mà người đó phải di chuyển theo x từ đó biểu diễn tổng thời gian.
+ Tìm giá trị nhỏ nhất của tổng thời gian đó (đưa về bài toán tìm giá trị nhỏ nhất trên đoạn đã học).
Lời giải chi tiết

Gọi vị trí hòn đảo là B và vị trí thuyền neo đậu trên bờ là C.
Ta cần tìm vị trí điểm C trên đoạn PA sao cho thời gian thuyền đi từ đảo vào bờ (đoạn BC) và đi bộ tiếp từ C đến thị trấn A (đoạn CA) là ngắn nhất.
Gọi đoạn PC = x (km) với \(0 \le x \le 12\).
Áp dụng định lý Pythagore trong tam giác BPC vuông tại P có: \(BC = \sqrt {{x^2} + 9} \) (km).
Thuyền đi với vận tốc 2,5 km/h nên thời gian đi hết đoạn BC là \(\frac{{\sqrt {{x^2} + 9} }}{{2,5}}\) (giờ).
Ta có: AC = PA – x = 12 – x (km).
Người đi bộ với vận tốc 4 km/h nên thời gian đi hết đoạn AC là \(\frac{{12 - x}}{4}\) (giờ).
Tổng thời gian người đó đi từ đảo đến thị trấn A là: \(T(x) = \frac{{\sqrt {{x^2} + 9} }}{{2,5}} + \frac{{12 - x}}{4}\) (giờ).
Bài toán trở thành tìm giá trị nhỏ nhất của hàm T(x) trên đoạn [0;12].
Ta có: \(T'(x) = \frac{{2x}}{{5\sqrt {{x^2} + 9} }} - \frac{1}{4}\).
\(T'(x) = 0 \Leftrightarrow \frac{{2x}}{{5\sqrt {{x^2} + 9} }} - \frac{1}{4} = 0 \Leftrightarrow 8x = 5\sqrt {{x^2} + 9} \).
Giải phương trình trên ta được \(x = \frac{{5\sqrt {39} }}{{13}} \approx 2,4\) là giá trị thỏa mãn điều kiện.
Bảng biến thiên:
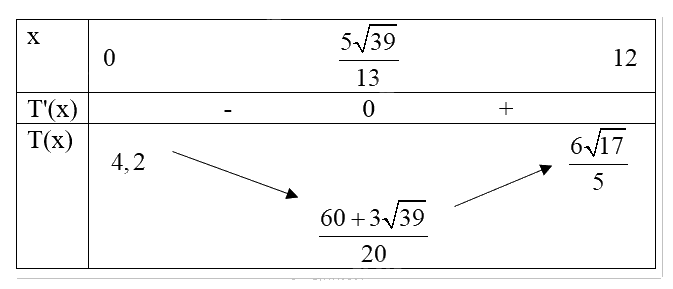
Vậy điểm neo đậu thuyền trên đoạn PA cách P khoảng 2,4 km để thời gian di chuyển là ngắn nhất.
Bài 1.44 trang 31 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 1.44 thường yêu cầu học sinh thực hiện các thao tác sau:
(Ở đây sẽ là lời giải chi tiết của bài 1.44, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ, nếu bài toán yêu cầu tìm đạo hàm của hàm số f(x) = x^3 - 3x^2 + 2, lời giải sẽ trình bày các bước sau:)
Bước 1: Tính đạo hàm f'(x)
f'(x) = 3x^2 - 6x
Bước 2: Tìm các điểm mà f'(x) = 0
3x^2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Bước 3: Xác định khoảng đơn điệu
Xét dấu f'(x) trên các khoảng:
Bước 4: Tìm cực trị
Tại x = 0, f'(x) đổi dấu từ dương sang âm => Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2
Tại x = 2, f'(x) đổi dấu từ âm sang dương => Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Bài 1.44 trang 31 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.