Bài 1.35 trang 25 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.35 trang 25 Sách bài tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau: a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\). b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Đề bài
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau:
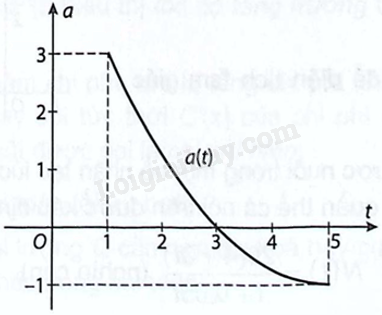
a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\).
b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Phương pháp giải - Xem chi tiết
Ý a:
+ \(a\left( t \right) = v'\left( t \right)\). Từ đồ thị xét dấu \(a\left( t \right)\) trên khoảng \(t \in \left[ {1;5} \right]\)
+ Lập bảng biến thiên của \(v\left( t \right)\).
Ý b: Từ bảng biến thiên suy ra được giá trị lớn nhất của vận tốc đạt được tại thời điểm nào.
Lời giải chi tiết
a) Ta có \(a\left( t \right) = v'\left( t \right)\).
Từ đồ thị ta có \(a\left( t \right) = 0 \Leftrightarrow t = 3\).
Ta thấy \(a\left( t \right) > 0\) với mọi \(t \in \left( {1;3} \right)\), \(a\left( t \right) < 0\) với mọi \(t \in \left( {3;5} \right)\).
Lập bảng biến thiên
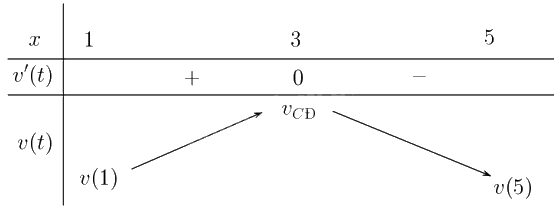
b) Từ bảng biến thiên suy ra vận tốc lớn nhất đạt tại giây thứ \(3\) (\(t = 3\)).
Bài 1.35 trang 25 Sách bài tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 1.35 yêu cầu học sinh tìm đạo hàm của hàm số cho trước. Hàm số có thể là một hàm số đơn giản hoặc một hàm số phức tạp được xây dựng từ các hàm số cơ bản bằng các phép toán cộng, trừ, nhân, chia, hợp thành.
Phương pháp giải:
Để giải bài tập này, học sinh cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số cần tìm đạo hàm là f(x) = x2 + 2x + 1. Ta có:
f'(x) = (x2)' + (2x)' + (1)' = 2x + 2 + 0 = 2x + 2
Lưu ý:
Khi tính đạo hàm của hàm số phức tạp, học sinh cần chú ý đến thứ tự thực hiện các phép toán. Đồng thời, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài giải chi tiết bài 1.35 trang 25 Sách bài tập Toán 12 - Kết nối tri thức:
(Nội dung giải bài tập cụ thể sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng. Bài giải sẽ được trình bày rõ ràng, dễ hiểu, có kèm theo các chú thích và giải thích cần thiết.)
Mở rộng kiến thức:
Ngoài việc giải bài tập, học sinh cũng nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế. Đạo hàm được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kinh tế, kỹ thuật,...
Bài tập tương tự:
Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Tổng kết:
Bài 1.35 trang 25 Sách bài tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán 12.
Các chủ đề liên quan: