Bài 1.4 trang 9 sách bài tập Toán 12 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và cách áp dụng chúng vào giải quyết bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.4 trang 9 sách bài tập Toán 12 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau: a) (y = {x^4} - 2{x^2} + 3); b) (y = {x^2}ln x).
Đề bài
Tìm các khoảng đơn điệu và các cực trị (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = {x^2}\ln x\).
Phương pháp giải - Xem chi tiết
Ý a:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Ý b:
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\).
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra các khoảng đồng biến, nghịch biến, cực trị của hàm số.
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = 4{x^3} - 4x\). Khi đó \(y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow {x^3} - x = 0 \Leftrightarrow x = - 1\) hoặc \(x = 0\) hoặc \(x = 1\).
Lập bảng biến thiên của hàm số:
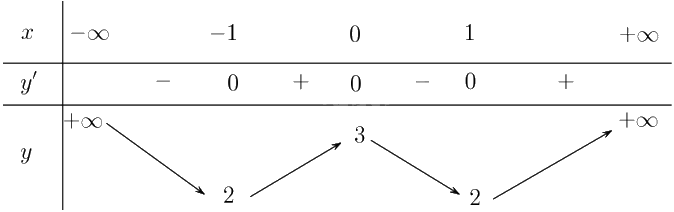
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đạt cực đại tại \(x = 0\) và \({y_{CĐ}} = y\left( { 0} \right) = 3\).
Hàm số đạt cực tiểu tại \(x = - 1\) và \({y_{CT}} = y\left( { - 1} \right) = 2\).
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 2\).
b) Tập xác định: \(\left( {0; + \infty } \right)\)
Ta có \(y' = 2x\ln x + x\). Khi đó \(y' = 0 \Leftrightarrow 2x\ln x + x = 0 \Leftrightarrow \ln x = - \frac{1}{2} \Leftrightarrow x = {e^{ - \frac{1}{2}}}\)
Lập bảng biến thiên của hàm số:
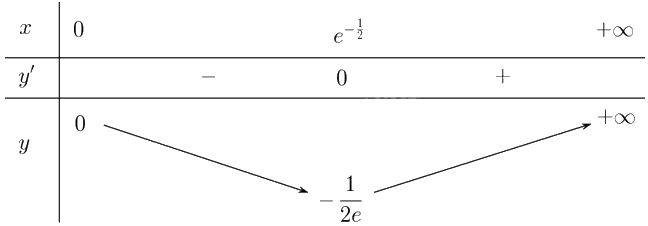
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng \(\left( {{e^{ - \frac{1}{2}}}; + \infty } \right)\). Hàm số nghịch biến trên khoảng \(\left( {0;{e^{ - \frac{1}{2}}}} \right)\).
Hàm số đạt cực tiểu tại \(x = {e^{ - \frac{1}{2}}}\) và \({y_{CT}} = y\left( {{e^{ - \frac{1}{2}}}} \right) = - \frac{1}{{2e}}\).
Bài 1.4 trang 9 sách bài tập Toán 12 Kết nối tri thức yêu cầu tính giới hạn của hàm số. Để giải bài này, chúng ta cần nắm vững định nghĩa giới hạn của hàm số tại một điểm và các tính chất của giới hạn.
Đề bài thường cho một hàm số f(x) và yêu cầu tính limx→a f(x). Trong đó, a là một số thực hoặc vô cực.
Có nhiều phương pháp để tính giới hạn, tùy thuộc vào dạng của hàm số:
Để cung cấp lời giải chi tiết, cần biết chính xác nội dung của bài 1.4 trang 9. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một ví dụ minh họa:
Ví dụ: Tính limx→2 (x2 - 4) / (x - 2)
Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 1.4 trang 9 sách bài tập Toán 12 Kết nối tri thức là một bài tập cơ bản về giới hạn. Việc nắm vững các khái niệm và phương pháp giải sẽ giúp bạn tự tin giải quyết các bài tập phức tạp hơn. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài tập và học Toán 12 hiệu quả hơn.
| Khái niệm | Giải thích |
|---|---|
| Giới hạn của hàm số | Giá trị mà hàm số tiến tới khi x tiến tới một giá trị nhất định. |
| Giới hạn một bên | Giới hạn của hàm số khi x tiến tới một giá trị từ bên trái hoặc bên phải. |