Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 24 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?
Đề bài
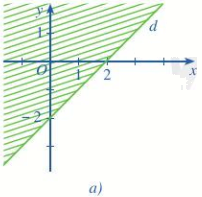
Nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?
Phương pháp giải - Xem chi tiết
Bước 1: Tìm phương trình đường thẳng dạng \(y = ax + b\)
Bước 2: Lấy điểm thuộc miền nghiệm trên đồ thị thay vào biểu thức \(ax + b - y\), nếu âm thì bất phương trình là \(ax - y + b < 0\), ngược lại thì bất phương trình là \(ax - y + b > 0\)
Lời giải chi tiết
a) Giả sử đường thẳng d có dạng y = ax + b
Vì đường thẳng d qua điểm (2;0) và (0;-2) nên ta có:
\(\left\{ \begin{array}{l}0 = 2a + b\\ - 2 = b\end{array} \right.\)
Suy ra, b = -2 và a = 1, tức y = x - 2
Vậy phương trình đường thẳng là \(x-y-2=0\)
Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0
=> Bất phương trình cần tìm là \(x - y - 2 > 0\)
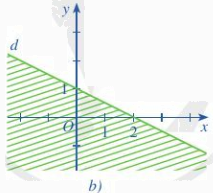
b) Đường thẳng qua điểm (2;0) và (0;1)
Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)
Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)
=> \(a = - \frac{1}{2},b = 1\)
=> phương trình đường thẳng là \(y = - \frac{1}{2}x + 1\)
Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0\)
=> Bất phương trình cần tìm là \( - \frac{1}{2}x - y + 1 < 0\)
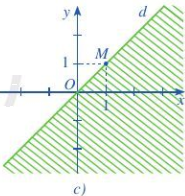
c) Đường thẳng qua điểm (0;0) và (1;1)
Thay x=0, y=0 vào phương trình \(y = ax + b\) ta được \(b=0\)
Thay x=1, y=1 vào phương trình \(y = ax + b\) ta được \(1 = a + b\)
Suy ra, a = 1, b = 0, tức y = x
Vậy phương trình đường thẳng là x-y=0
Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0
=> Bất phương trình cần tìm là \(x - y < 0\)
Bài 3 trang 24 SGK Toán 10 tập 1 – Cánh diều thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) và các tính chất của chúng để giải quyết các bài toán cụ thể.
Bài 3 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Đề bài: Cho A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm A ∪ B.
Lời giải:
A ∪ B là tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai).
Do đó, A ∪ B = {0; 1; 2; 3; 4; 5; 6}.
Đề bài: Cho A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm A ∩ B.
Lời giải:
A ∩ B là tập hợp chứa tất cả các phần tử thuộc cả A và B.
Do đó, A ∩ B = {2; 3; 4; 5}.
Đề bài: Cho A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm A \ B.
Lời giải:
A \ B là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
Do đó, A \ B = {0; 1}.
Đề bài: Cho A = {0; 1; 2; 3; 4; 5} và B = {2; 3; 4; 5; 6}. Tìm B \ A.
Lời giải:
B \ A là tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A.
Do đó, B \ A = {6}.
Ngoài bài 3, chương 1 còn có nhiều bài tập tương tự về tập hợp. Để nắm vững kiến thức, bạn nên luyện tập thêm các bài tập sau:
Để giải tốt các bài tập về tập hợp, bạn cần:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã hiểu rõ cách giải bài 3 trang 24 SGK Toán 10 tập 1 – Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục kiến thức. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải Toán 10 và các môn học khác.