Bài học này cung cấp lý thuyết đầy đủ về các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm, thuộc chương trình SGK Toán 10 Cánh diều. Chúng ta sẽ cùng tìm hiểu về ý nghĩa, cách tính và ứng dụng của các đại lượng này trong thống kê.
Nắm vững kiến thức này là bước quan trọng để hiểu sâu hơn về sự biến động của dữ liệu và đưa ra những phân tích chính xác trong các bài toán thực tế.
A. Lý thuyết 1. Khoảng biến thiên, khoảng tứ phân vị a) Định nghĩa
A. Lý thuyết
1. Khoảng biến thiên, khoảng tứ phân vị
a) Định nghĩa
- Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó. Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau: \(R = {x_{\max }} - {x_{\min }}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\) là giá trị nhỏ nhất của mẫu số liệu đó. - Giả sử \({Q_1}\), \({Q_2}\), \({Q_3}\) là tứ phân vị của mẫu số liệu. Ta gọi hiệu \({\Delta _Q} = {Q_3} - {Q_1}\) là khoảng tứ phân vị của mẫu số liệu đó. |
b) Ý nghĩa
- Khoảng biến thiên:
+ Phản ánh sự “dao động”, “sự dàn trải” của các số liệu trong mẫu.
+ Là đại lượng dễ hiểu, dễ tính toán và tương đối tốt với các mẫu số liệu nhỏ.
+ Chưa diễn giải đầy đủ sự phân tán của các số liệu trong mẫu.
+ Bị ảnh hưởng bởi các giá trị bất thường.
- Khoảng tứ phân vị:
+ Cho biết mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp.
+ Có thể giúp xác định các giá trị bất thường.
2. Phương sai
a) Định nghĩa
Cho mẫu số liệu thống kê có n giá trị \({x_1},{x_2},...,{x_n}\) và số trung bình cộng là \(\overline x \). Ta gọi số \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n}\) là phương sai của mẫu số liệu trên. |
b) Ý nghĩa
Phương sai là số đặc trưng đo mức độ phân tán của mẫu số liệu. Mẫu số liệu nào có phương sai nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.
3. Độ lệch chuẩn
a) Định nghĩa
| Căn bậc hai số học của phương sai gọi là độ lệch chuẩn của mẫu số liệu thống kê. |
Nhận xét: Vì độ lệch chuẩn có cùng đơn vị đo với số liệu thống kê nên khi cần chú ý đến đơn vị đo thì ta sử dụng độ lệch chuẩn mà không sử dụng phương sai.
b) Ý nghĩa
Cũng như phương sai, khi hai mẫu số liệu thống kê có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn. Độ lệch chuẩn là số đặc trưng đo mức độ phân tán của mẫu số liệu thống kê có cùng đơn vị đo.
4. Tính hợp lí của số liệu thống kê
Ta có thể sử dụng các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm để chỉ ra được những số liệu bất thường của mẫu số liệu đó. Ta thường sử dụng khoảng tứ phân vị để xác định số liệu bất thường của mẫu số liệu. Cụ thể như sau:
Giả sử \({Q_1}\), \({Q_2}\), \({Q_3}\) là tứ phân vị của mẫu số liệu và hiệu \({\Delta _Q} = {Q_3} - {Q_1}\) là khoảng tứ phân vị của mẫu số liệu đó. Một giá trị của mẫu số liệu được coi là một giá trị bất thường nếu nó nhỏ hơn \({Q_1} - \frac{3}{2}{\Delta _Q}\) hoặc lớn hơn \({Q_3} + \frac{3}{2}{\Delta _Q}\). |
B. Bài tập
Bài 1: Mẫu số liệu thống kê chiều cao (đơn vị: mét) của 15 cây bạch đàn là:
6,3 6,6 8,2 8,3 7,8 7,9 9,0 8,9 7,2 7,5 8,7 7,7 8,8 7,6
a) Tìm khoảng biến thiên của mẫu số liệu.
b) Tìm khoảng tứ phân vị của mẫu số liệu.
Giải:
a) Trong mẫu số liệu, số lớn nhất là 9,0 và số bé nhất là 6,3. Vậy khoảng biến thiên của mẫu số liệu là:
\(R = {x_{\max }} - {x_{\min }} = 9,0 - 6,3 = 2,7\) (m).
b) Sắp xếp các số liệu của mẫu theo thứ tự không giảm, ta được:
6,3 6,6 7,2 7,5 7,5 7,6 7,7 7,8 7,9 8,2 8,3 8,7 8,8 8,9 9,0
Do đó \({Q_1} = 7,5\) (m); \({Q_2} = 7,8\) (m); \({Q_3} = 8,7\) (m).
Vậy khoảng tứ phân vị của mẫu số liệu là:
\({\Delta _Q} = {Q_3} - {Q_1} = 8,7 - 7,5 = 1,2\) (m).
Bài 2: Bảng dưới đây thống kê nhiệt độ (đơn vị: \(^oC\)) ở Thành phố Hồ Chí Minh ngày 3/6/2021 sau một số lần đo.

Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu trên.
Giải:
Nhiệt độ trung bình là:
\(\overline x = \frac{{27 + 26 + 28 + 32 + 34 + 35 + 30 + 28}}{8} = 30\) \({(^o}C)\).
Phương sai của mẫu số liệu là:
\({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + {{({x_3} - \overline x )}^2} + {{({x_4} - \overline x )}^2} + {{({x_5} - \overline x )}^2} + {{({x_6} - \overline x )}^2} + {{({x_7} - \overline x )}^2} + {{({x_8} - \overline x )}^2}}}{n}\)
\( = \frac{{{{( - 3)}^2} + {{( - 4)}^2} + {{( - 2)}^2} + {2^2} + {4^2} + {5^2} + {0^2} + {{( - 2)}^2}}}{8} = \frac{{78}}{8} = 9,75\).
Độ lệch chuẩn của mẫu số liệu đó là: \(s = \sqrt {9,75} \approx 3,12\) \({(^o}C)\).
Bài 3: Nếu các giá trị bất thường của mẫu số liệu thống kê sau:
5 6 19 21 22 23 24 25 26 27 28 29 30 31 32 33 34 48 49
Giải:
Mẫu số liệu có tứ phân vị là \({Q_1} = 22\), \({Q_2} = 27\), \({Q_3} = 32\).
Suy ra \({\Delta _Q} = {Q_3} - {Q_1} = 32 - 22 = 10\).
Ta có \({Q_1} - \frac{3}{2}{\Delta _Q} = 22 - \frac{3}{2}.10 = 7\), \({Q_3} + \frac{3}{2}{\Delta _Q} = 32 + \frac{3}{2}.10 = 47\).
Vậy các giá trị 5, 6 (nhỏ hơn 7) và 48, 49 (lớn hơn 47) là các giá trị bất thường của mẫu số liệu.
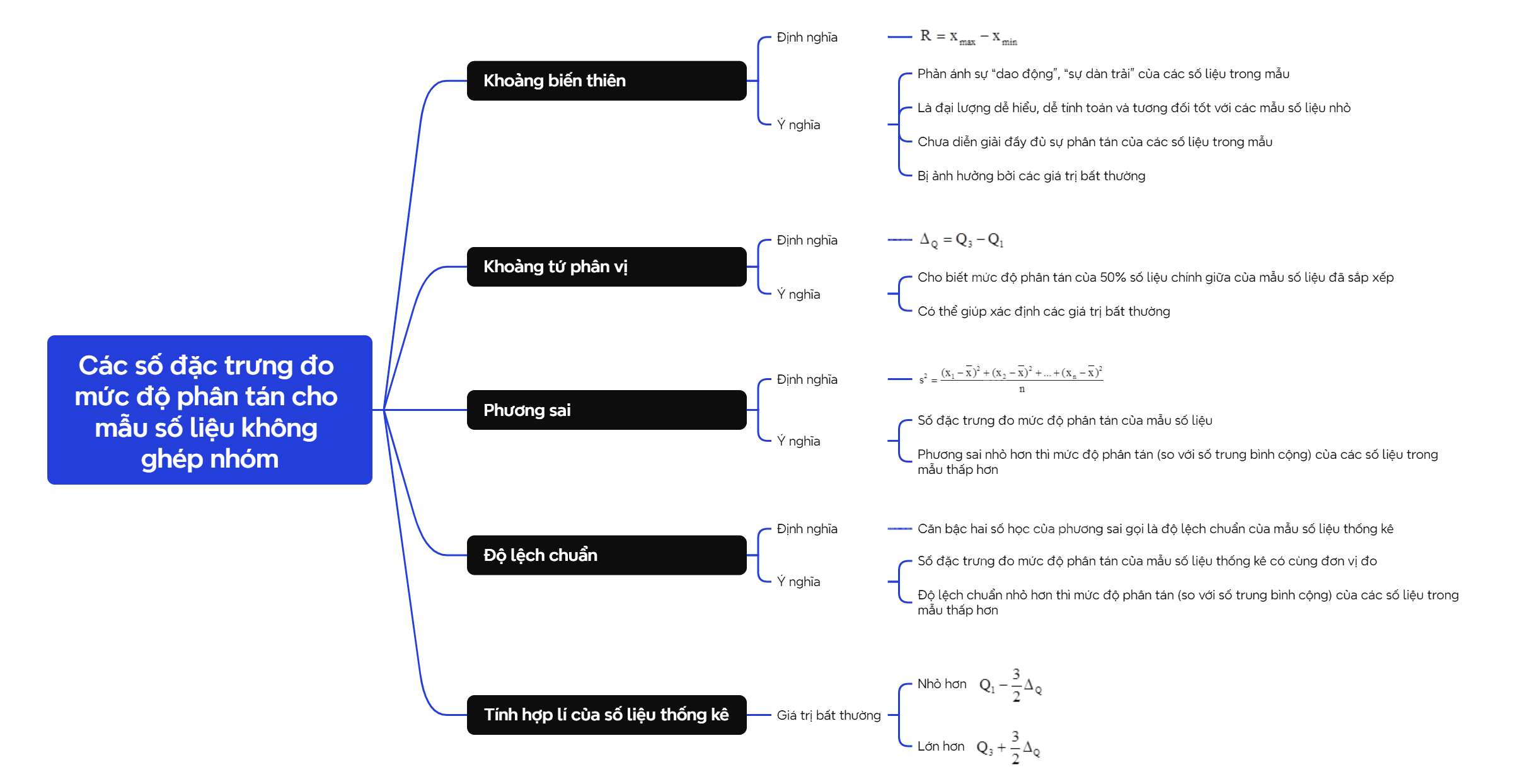
Trong thống kê, việc mô tả một tập dữ liệu không chỉ dừng lại ở việc tìm các giá trị trung tâm như trung bình cộng, trung vị, mốt. Để hiểu rõ hơn về sự phân tán của dữ liệu, chúng ta cần sử dụng các số đặc trưng đo mức độ phân tán. Bài viết này sẽ trình bày chi tiết về các số đặc trưng này trong chương trình SGK Toán 10 Cánh diều.
Mức độ phân tán thể hiện sự khác biệt giữa các giá trị trong một tập dữ liệu. Một tập dữ liệu có mức độ phân tán lớn cho thấy các giá trị trong tập dữ liệu đó rải rác, không tập trung. Ngược lại, một tập dữ liệu có mức độ phân tán nhỏ cho thấy các giá trị trong tập dữ liệu đó tập trung gần nhau.
Có ba số đặc trưng chính được sử dụng để đo mức độ phân tán của một mẫu số liệu không ghép nhóm:
Giả sử ta có mẫu số liệu không ghép nhóm: x1, x2, ..., xn.
Xét mẫu số liệu sau: 2, 4, 6, 8, 10.
Bước 1: Tính trung bình cộng
x̄ = (2 + 4 + 6 + 8 + 10) / 5 = 6
Bước 2: Tính phương sai
s2 = [(2-6)2 + (4-6)2 + (6-6)2 + (8-6)2 + (10-6)2] / (5-1) = (16 + 4 + 0 + 4 + 16) / 4 = 10
Bước 3: Tính độ lệch chuẩn
s = √10 ≈ 3.16
Bước 4: Tính độ biến thiên
R = 10 - 2 = 8
Các số đặc trưng đo mức độ phân tán giúp chúng ta:
Các số đặc trưng đo mức độ phân tán được ứng dụng rộng rãi trong nhiều lĩnh vực, như:
Khi sử dụng các số đặc trưng đo mức độ phân tán, cần lưu ý:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm - SGK Toán 10 Cánh diều. Chúc bạn học tốt!