Chào mừng bạn đến với bài học về Lý thuyết Phương trình đường thẳng trong chương trình SGK Toán 10 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về phương trình đường thẳng, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng tôi sẽ trình bày một cách rõ ràng, dễ hiểu, kèm theo các ví dụ minh họa cụ thể để bạn có thể nắm bắt kiến thức một cách nhanh chóng và sâu sắc.
A. Lý thuyết 1. Phương trình tham số của đường thẳng a) Vecto chỉ phương của đường thẳng
A. Lý thuyết
1. Phương trình tham số của đường thẳng
a) Vecto chỉ phương của đường thẳng
| Vecto \(\overrightarrow u \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu \(\overrightarrow u \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow u \) song song hoặc trùng với \(\Delta \). |
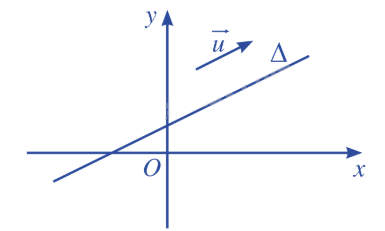
Nhận xét:
- Nếu \(\overrightarrow u \) là một vecto chỉ phương của \(\Delta \) thì \(k\overrightarrow u \) \((k \ne 0)\) cũng là một vecto chỉ phương của \(\Delta \).
- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto chỉ phương của đường thẳng đó.
b) Phương trình tham số của đường thẳng
| Hệ \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + at\end{array} \right.\) (\({a^2} + {b^2} > 0\) và t là tham số) được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow u = (a;b)\) làm vecto chỉ phương. |
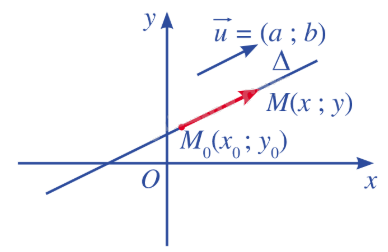
Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng \(\Delta \). Ngược lại, với mỗi điểm trên đường thẳng \(\Delta \), ta xác định được một giá trị cụ thể của t.
2. Phương trình tổng quát của đường thẳng
a) Vecto pháp tuyến của đường thẳng
| Vecto \(\overrightarrow n \) được gọi là vecto pháp tuyến của đường thẳng \(\Delta \) nếu \(\overrightarrow n \ne \overrightarrow 0 \) và giá của vecto \(\overrightarrow n \) vuông góc với \(\Delta \). |
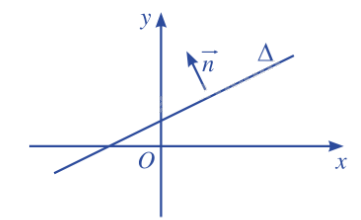
Nhận xét:
- Nếu \(\overrightarrow n \) là một vecto pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \) \((k \ne 0)\) cũng là một vecto pháp tuyến của \(\Delta \).
- Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vecto pháp tuyến của đường thẳng đó.
b) Phương trình tổng quát của đường thẳng
| Phương trình \(ax + by + c = 0\) (a và b không đồng thời bằng 0) được gọi là phương trình tổng quát của đường thẳng. |
Nhận xét:
- Đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow n = (a;b)\) làm vecto pháp tuyến có phương trình là \(a(x - {x_0}) + b(y - {y_0}) = 0 \Leftrightarrow ax + by + ( - a{x_0} - b{y_0}) = 0\).
- Mỗi phương trình \(ax + by + c = 0\) (a và b không đồng thời bằng 0) đều xác định một đường thẳng \(\Delta \) trong mặt phẳng tọa độ nhận một vecto pháp tuyến là \(\overrightarrow n = (a;b)\).
c) Những dạng đặc biệt của phương trình tổng quát
- Đường thẳng \(\Delta \) có phương trình tổng quát \(ax + by + c = 0\) (a hoặc b khác 0) là đồ thị hàm số bậc nhất khi và chỉ khi \(a \ne 0\) và \(b \ne 0\).
- Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.
3. Lập phương trình đường thẳng
Khi lập phương trình đường thẳng, ta thường gặp ba trường hợp như sau:
– Đi qua một điểm cho trước và biết vecto pháp tuyến.
– Đi qua một điểm cho trước và biết vecto chỉ phương.
– Đi qua hai điểm cho trước.
a) Lập phương trình đường thẳng đi qua một điểm và biết vecto pháp tuyến
| Đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow n = (a;b)\) làm vecto pháp tuyến có phương trình là \(a(x - {x_0}) + b(y - {y_0}) = 0\). |
b) Lập phương trình đường thẳng đi qua một điểm và biết vecto chỉ phương
Phương trình đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và nhận \(\overrightarrow u = (a;b)\) \((\overrightarrow u \ne \overrightarrow 0 )\) làm vecto chỉ phương là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) (t là tham số). Nếu \(a \ne 0\) và \(b \ne 0\) thì ta còn có thể viết phương trình của đường thẳng \(\Delta \) ở dạng: \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}\). |
c) Lập phương trình đường thẳng đi qua hai điểm
Đường thẳng \(\Delta \) đi qua \(A({x_A};{y_A})\), \(B({x_B};{y_B})\) nên nhận vecto \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\) làm vecto chỉ phương. Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = {x_A} + ({x_B} - {x_A})t\\y = {y_A} + ({y_B} - {y_A})t\end{array} \right.\) (t là tham số). Nếu \({x_B} - {x_A} \ne 0\) và \({y_B} - {y_A} \ne 0\) thì ta có thể viết phương trình đường thẳng \(\Delta \) dưới dạng: \(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}}\). |
4. Phương trình đoạn chắn
Đường thẳng \(\Delta \) cắt trục Ox, Oy lần lượt tại A(a;0) và B(0;b) có phương trình đoạn chắn là: \(\frac{x}{a} + \frac{y}{b} = 1\) \((ab \ne 0)\). |
B. Bài tập
Lập phương trình đường thẳng \(\Delta \) thỏa mãn:
a) Đi qua M(-2;-3) và có \(\overrightarrow n = (2;5)\) là vecto pháp tuyến.
b) Đi qua M(3;-5) và có \(\overrightarrow u = (2; - 4)\) là vecto chỉ phương.
c) Đi qua A(-3;4) và B(1;-1).
Giải:
a) Phương trình \(\Delta \) là \(2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0\).
b) Phương trình \(\Delta \) là \(\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0\).
c) Phương trình \(\Delta \) là \(\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0\).
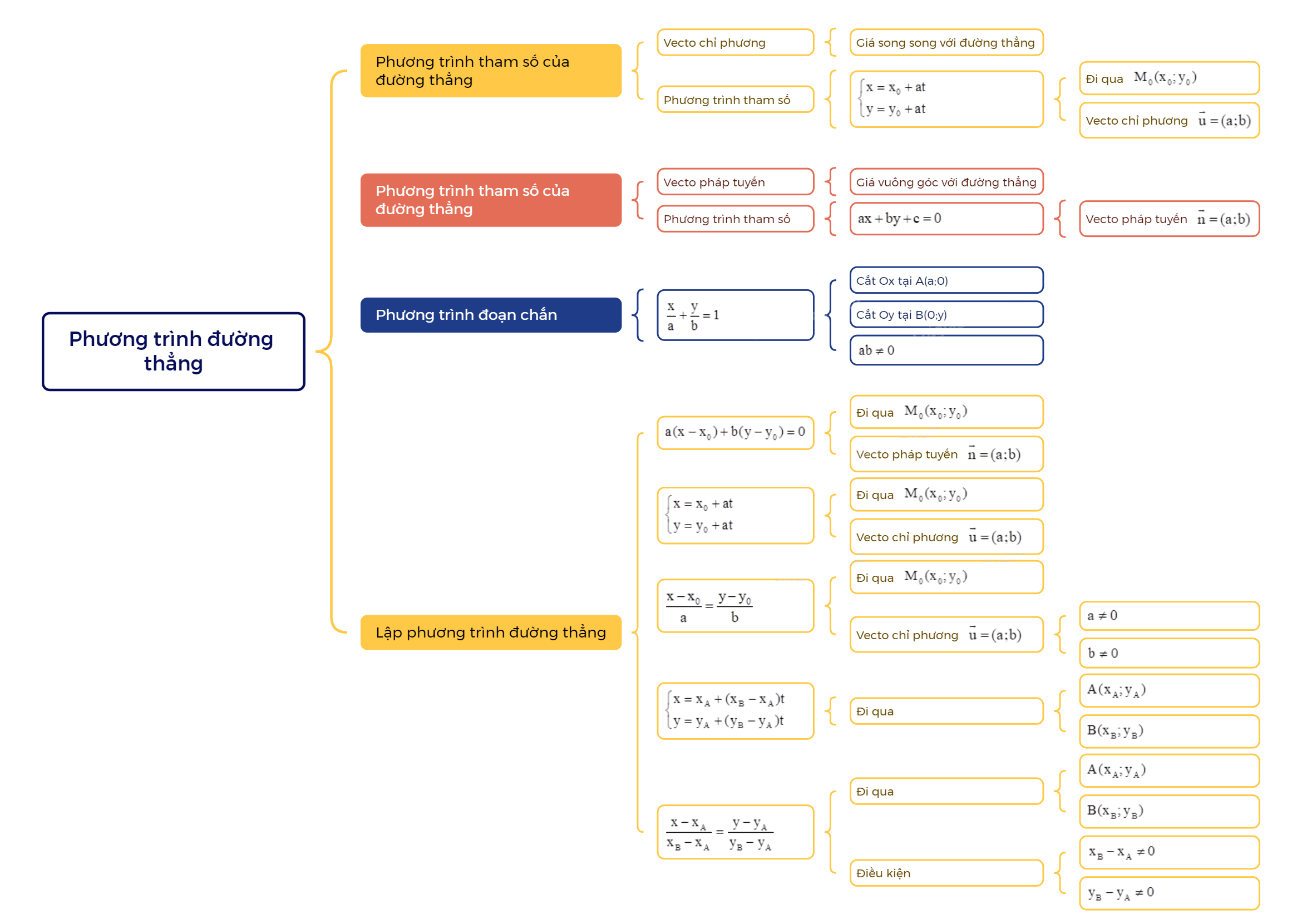
Phương trình đường thẳng là một khái niệm cơ bản và quan trọng trong hình học giải tích lớp 10. Hiểu rõ lý thuyết này là nền tảng để giải quyết nhiều bài toán liên quan đến đường thẳng, khoảng cách, và các khái niệm hình học khác.
Phương trình tổng quát của đường thẳng là: ax + by + c = 0, trong đó a, b không đồng thời bằng 0. a và b là các hệ số của x và y, c là hằng số tự do.
Ngoài dạng tổng quát, phương trình đường thẳng còn có các dạng đặc biệt:
Hệ số góc k của đường thẳng y = kx + b thể hiện độ dốc của đường thẳng. k > 0: đường thẳng đi lên; k < 0: đường thẳng đi xuống; k = 0: đường thẳng song song với trục Ox.
Xét hai đường thẳng:
d1: a1x + b1y + c1 = 0
d2: a2x + b2y + c2 = 0
Ta có:
Khoảng cách d từ điểm M(x0, y0) đến đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
d = |ax0 + by0 + c| / √(a2 + b2)
Ví dụ 1: Viết phương trình đường thẳng đi qua điểm A(1, 2) và có hệ số góc k = -3.
Giải: Áp dụng công thức y - y0 = k(x - x0), ta có: y - 2 = -3(x - 1) => y - 2 = -3x + 3 => 3x + y - 5 = 0
Ví dụ 2: Tìm khoảng cách từ điểm B(0, 1) đến đường thẳng 2x - y + 3 = 0.
Giải: Áp dụng công thức tính khoảng cách, ta có: d = |2(0) - 1 + 3| / √(22 + (-1)2) = 2 / √5 = 2√5 / 5
Để nắm vững kiến thức về phương trình đường thẳng, bạn nên luyện tập thêm nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, phong phú, kèm theo đáp án chi tiết để bạn có thể tự học và kiểm tra kiến thức của mình.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều. Chúc bạn học tập tốt!