Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
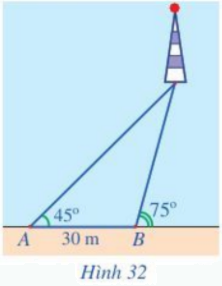
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75
Đề bài
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải - Xem chi tiết
Gọi C là vị trí ngọn hải đăng, H là hình chiếu của C trên AB.
Bước 1: Tính góc ACB, ABC.
Bước 2: Tính AC bằng cách áp dụng định lí sin trong tam giác ABC: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
Bước 3: Tính AH bằng công thức: AH = AC. cos A.
Lời giải chi tiết
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
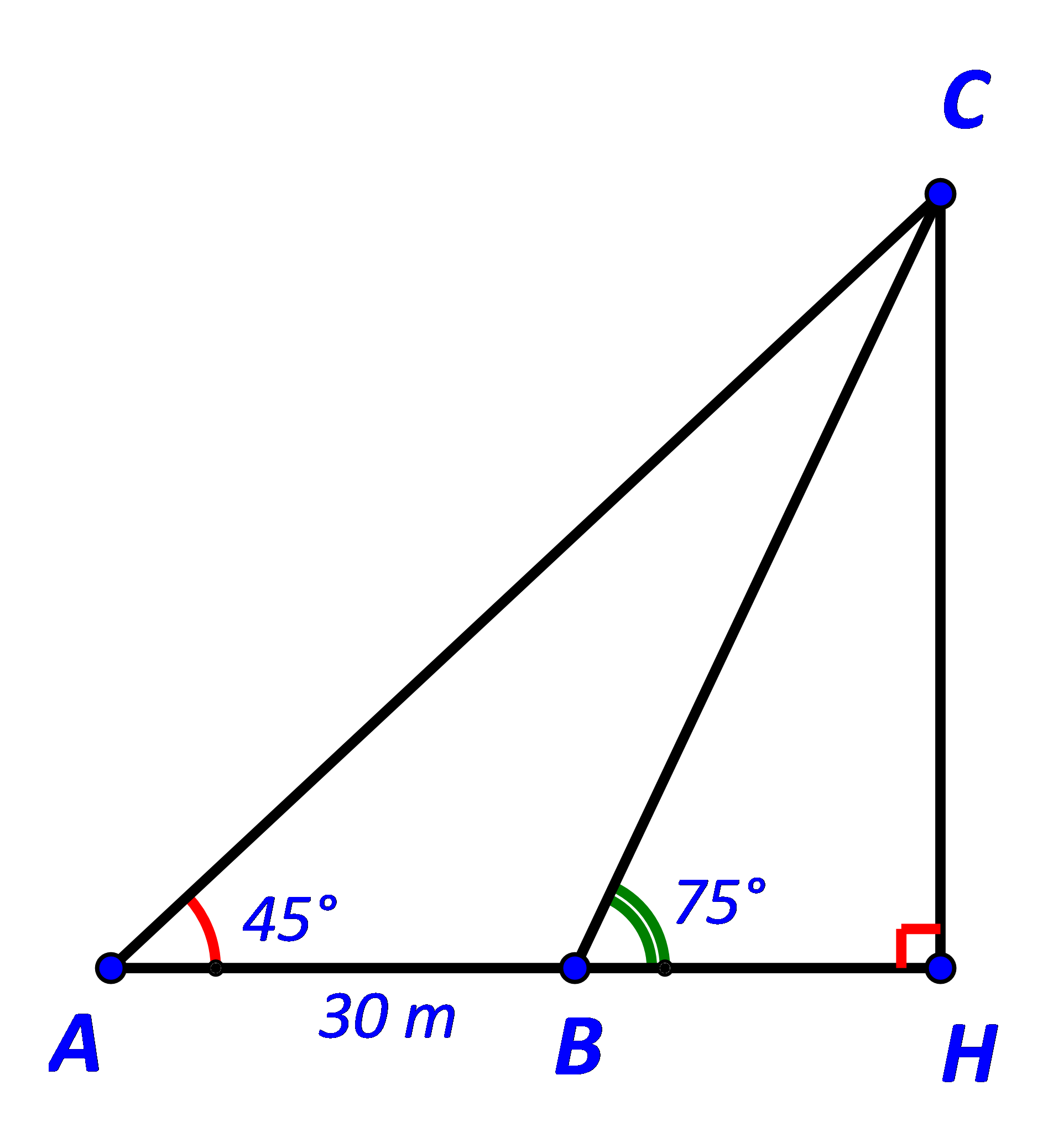
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.
Bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 7, trang 77, SGK Toán 10 tập 1 – Cánh diều. Ví dụ:)
Đề bài: Cho hình bình hành ABCD. Tìm vectơ bằng vectơ AB.
Lời giải:
Trong hình bình hành ABCD, ta có AB = DC và AB // DC. Do đó, vectơ DC bằng vectơ AB. Ngoài ra, ta cũng có AD = BC và AD // BC, nên vectơ BC bằng vectơ AD.
Đề bài: Cho tam giác ABC. Tìm vectơ bằng vectơ CA.
Lời giải:
Trong tam giác ABC, không có vectơ nào bằng vectơ CA. Tuy nhiên, ta có vectơ AC = -CA, tức là vectơ AC và vectơ CA ngược chiều nhau và có cùng độ dài.
Để giải các bài tập về vectơ một cách hiệu quả, các em cần lưu ý những điều sau:
Để củng cố kiến thức về vectơ, các em có thể tham khảo thêm các bài tập tương tự sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập vectơ được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc giải bài 7 trang 77 SGK Toán 10 tập 1 – Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |