Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Hai lực F1 ,F2 cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc
Đề bài
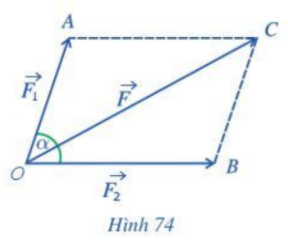
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = \alpha \) làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực \(\overrightarrow F \) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) làm cho vật di chuyển).
Phương pháp giải - Xem chi tiết
+) OACB là hình bình hành thì \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
+) Tính cường độ của hợp lực \(\overrightarrow F \) bằng định lí cosin: \(O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A\)
Lời giải chi tiết
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\\begin{array}{l} \Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\ \Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha \end{array}\\{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }\end{array}\)
Bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Bài tập này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán liên quan đến vectơ, đặc biệt là trong việc chứng minh các đẳng thức vectơ và xác định vị trí tương đối của các điểm.
Bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích, và kết luận. Ví dụ:)
(Giả sử câu a) yêu cầu chứng minh đẳng thức vectơ AB = CD)
Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể tham khảo một số bài tập tương tự sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!