Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục III trang 80, 81 SGK Toán 10 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục III tập trung vào các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học.
Cho tam giác ABC. Vẽ điểm D thỏa mãn AD =BC Tứ giác ABCD là hình gì?
Cho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {AD} = \overrightarrow {BC} .\) Tứ giác ABCD là hình gì?
Phương pháp giải:
Hai vectơ \(\overrightarrow {AD} ,\;\overrightarrow {BC} \)bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AD} = \overrightarrow {BC} .\)
\( \Rightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
Do đó tứ giác ABCD có một cặp cạnh đối song và bằng nhau
Vậy tứ giác ABCD là hình bình hành.
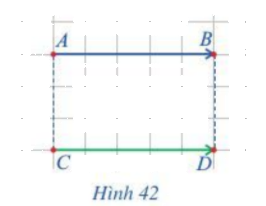
Quan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
Phương pháp giải:
a) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), chỉ ra chúng cùng phương.
b) Nhận xét về hướng của hai vectơ đó (hướng sang phải/trái)
c) Độ dài của vectơ \(\overrightarrow {AB} \) là độ dài đoạn thẳng AB.
Lời giải chi tiết:
a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
Cho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {AD} = \overrightarrow {BC} .\) Tứ giác ABCD là hình gì?
Phương pháp giải:
Hai vectơ \(\overrightarrow {AD} ,\;\overrightarrow {BC} \)bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết:
Ta có: \(\overrightarrow {AD} = \overrightarrow {BC} .\)
\( \Rightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
Do đó tứ giác ABCD có một cặp cạnh đối song và bằng nhau
Vậy tứ giác ABCD là hình bình hành.
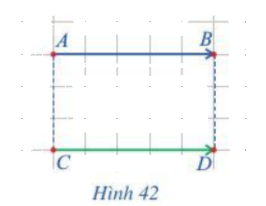
Quan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
Phương pháp giải:
a) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), chỉ ra chúng cùng phương.
b) Nhận xét về hướng của hai vectơ đó (hướng sang phải/trái)
c) Độ dài của vectơ \(\overrightarrow {AB} \) là độ dài đoạn thẳng AB.
Lời giải chi tiết:
a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
Mục III trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc củng cố và mở rộng kiến thức về vectơ, bao gồm các phép toán cơ bản như cộng, trừ vectơ, nhân vectơ với một số thực, và ứng dụng của vectơ trong việc giải quyết các bài toán hình học phẳng. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng cho việc học tập các chương trình Toán học ở các lớp trên.
Mục III bao gồm các bài tập vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến:
Để tìm vectơ chỉ phương của một đường thẳng, ta có thể sử dụng hai điểm nằm trên đường thẳng đó. Vectơ chỉ phương của đường thẳng đi qua hai điểm A(xA, yA) và B(xB, yB) là vectơ AB = (xB - xA, yB - yA).
Ba điểm A, B, C thẳng hàng khi và chỉ khi vectơ AB và AC cùng phương, tức là tồn tại một số k sao cho AC = kAB. Điều này có nghĩa là tỉ số giữa các tọa độ tương ứng của hai vectơ phải bằng nhau: xC - xA = k(xB - xA) và yC - yA = k(yB - yA).
Để tìm tọa độ điểm M thỏa mãn điều kiện cho trước, ta thường sử dụng các phép toán vectơ. Ví dụ, nếu M là trung điểm của đoạn thẳng AB, thì tọa độ của M là trung bình cộng của tọa độ của A và B: M((xA + xB)/2, (yA + yB)/2).
Vectơ không chỉ là một khái niệm trừu tượng trong Toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như Vật lý, Kỹ thuật, và Khoa học máy tính. Ví dụ, trong Vật lý, vectơ được sử dụng để biểu diễn các đại lượng vật lý như vận tốc, gia tốc, lực. Trong Kỹ thuật, vectơ được sử dụng để mô tả các chuyển động của robot và các hệ thống điều khiển.
Hy vọng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục III trang 80, 81 SGK Toán 10 tập 1 - Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng về vectơ, và đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn.