Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 54 SGK Toán 10 tập 2 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
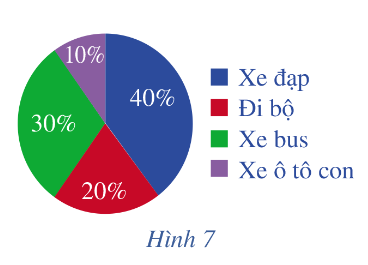
Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7.
Đề bài
Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7.
a) Có bao nhiêu bạn đi xe đạp đến trường?
b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường. Tính xác suất của biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.
Phương pháp giải - Xem chi tiết
a) Số bạn đi xe đạp = Số học sinh cả lớp nhân với tỉ lệ phần trăm số học sinh đi xe đạp
b) Bước 1: Tính số phần tử của không gian mẫu “\(n\left( \Omega \right)\)” và số phần tử của kết quả có lợi cho biến cố “\(n\left( A \right)\)” trong đó A là biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.
Bước 2: Xác suất của biến cố là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Lời giải chi tiết
a) Số bạn đi xe đạp đến trường là: \(40.40\% = 16\) ( học sinh )
b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường từ 40 bạn ta được một tổ hợp chập 1 của 40 phần tử. Do đó, không gian mẫu \(n\left( \Omega \right) = C_{40}^1\)( phần tử)
Gọi A là biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.
Để chọn 1 bạn học là bạn đến trường bằng xe đạp ta được một tổ hợp chập 1 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^1\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^1}}{{C_{40}^1}} = \frac{2}{5}\)
Bài 4 trang 54 SGK Toán 10 tập 2 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong mặt phẳng để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 4 trang 54 SGK Toán 10 tập 2 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Lưu ý: Vì độ dài yêu cầu là 1000 từ, phần này sẽ được mở rộng với các ví dụ cụ thể và giải thích chi tiết từng bước.)
Cho A(1; 2) và B(3; 4). Tìm tọa độ của vectơ AB.
Lời giải:
Tọa độ của vectơ AB được tính theo công thức: AB = (xB - xA; yB - yA). Thay các giá trị của A và B vào công thức, ta có:
AB = (3 - 1; 4 - 2) = (2; 2)
Cho vectơ a = (1; -2) và vectơ b = (3; 1). Tính a + b và 2a.
Lời giải:
a + b = (1 + 3; -2 + 1) = (4; -1)
2a = (2 * 1; 2 * -2) = (2; -4)
Cho A, B, C là ba điểm bất kỳ. Chứng minh rằng: AB + BC = AC.
Lời giải:
Sử dụng quy tắc cộng vectơ, ta có: AB + BC là vectơ nối từ A đến C, tức là AC. Do đó, AB + BC = AC.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 54 SGK Toán 10 tập 2 – Cánh diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng các kiến thức về vectơ vào giải quyết các bài toán hình học. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc chinh phục môn Toán.