Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 10 Cánh diều, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục II trong chương trình Toán 10 tập 1 tập trung vào các kiến thức về tập hợp, số thực và các phép toán cơ bản. Việc giải các bài tập trong mục này là vô cùng quan trọng để các em hiểu rõ lý thuyết và rèn luyện kỹ năng giải toán.
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
Lập bảng biến thiên của mỗi hàm số sau:
a) \(y = {x^2} - 3x + 4\)
b) \(y = - 2{x^2} + 5\)
Phương pháp giải:
- Xác định hệ số a, b.
- Tính \( - \frac{b}{{2a}}\).
- Tìm khoảng đồng biến, nghịch biến.
Lời giải chi tiết:
a) Hệ số \(a = 1 > 0,b = - 3 \Rightarrow \frac{{ - b}}{{2a}} = \frac{3}{2}\)
Vậy hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{3}{2}} \right)\) và đồng biến trên \(\left( {\frac{3}{2}; + \infty } \right)\)
b) Ta có \(a = - 2 < 0,b = 0\)
\( \Rightarrow - \frac{b}{{2a}} = 0\)
Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số \(y = {x^2} + 2x - 3\).
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy.
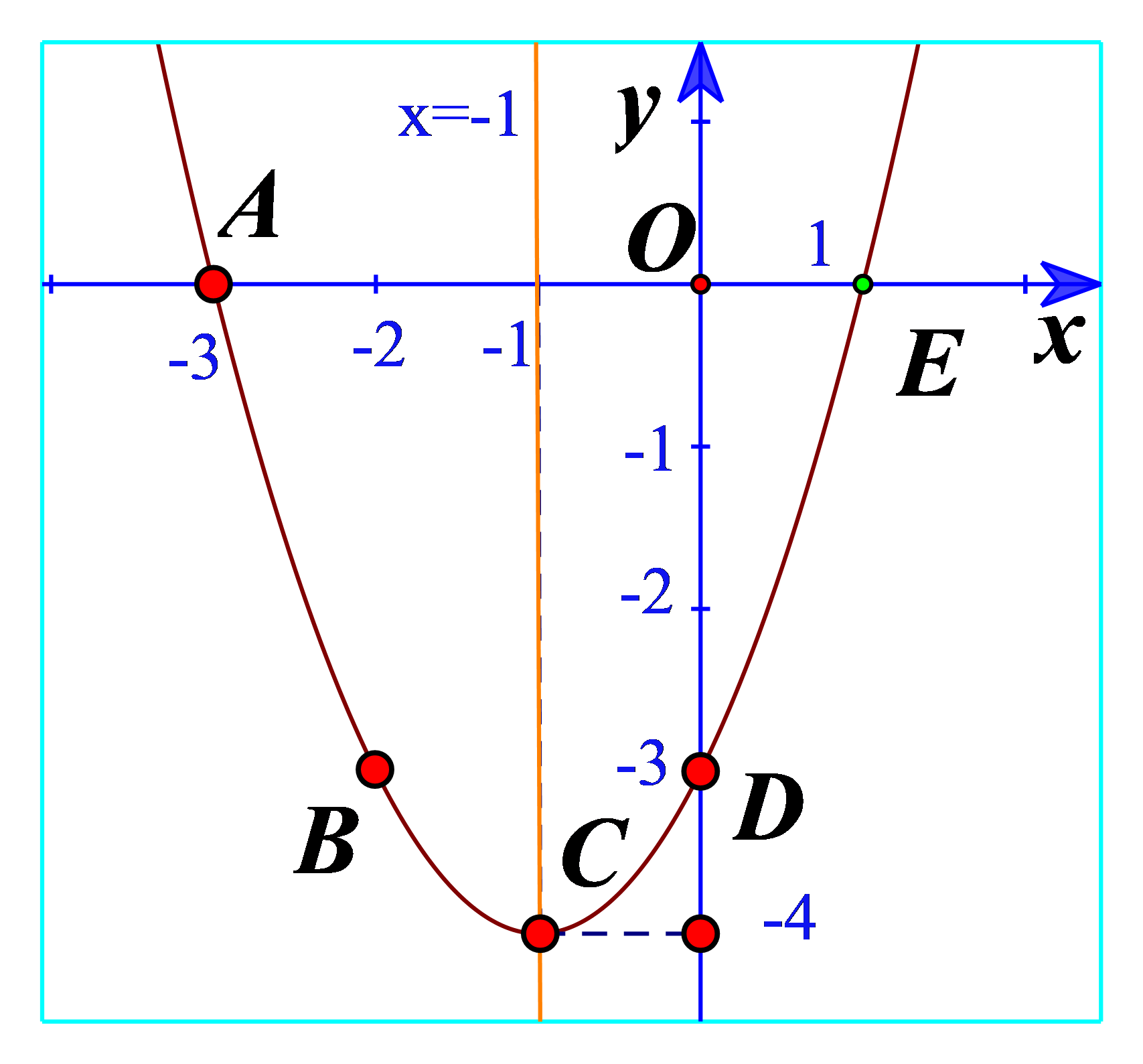
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11).
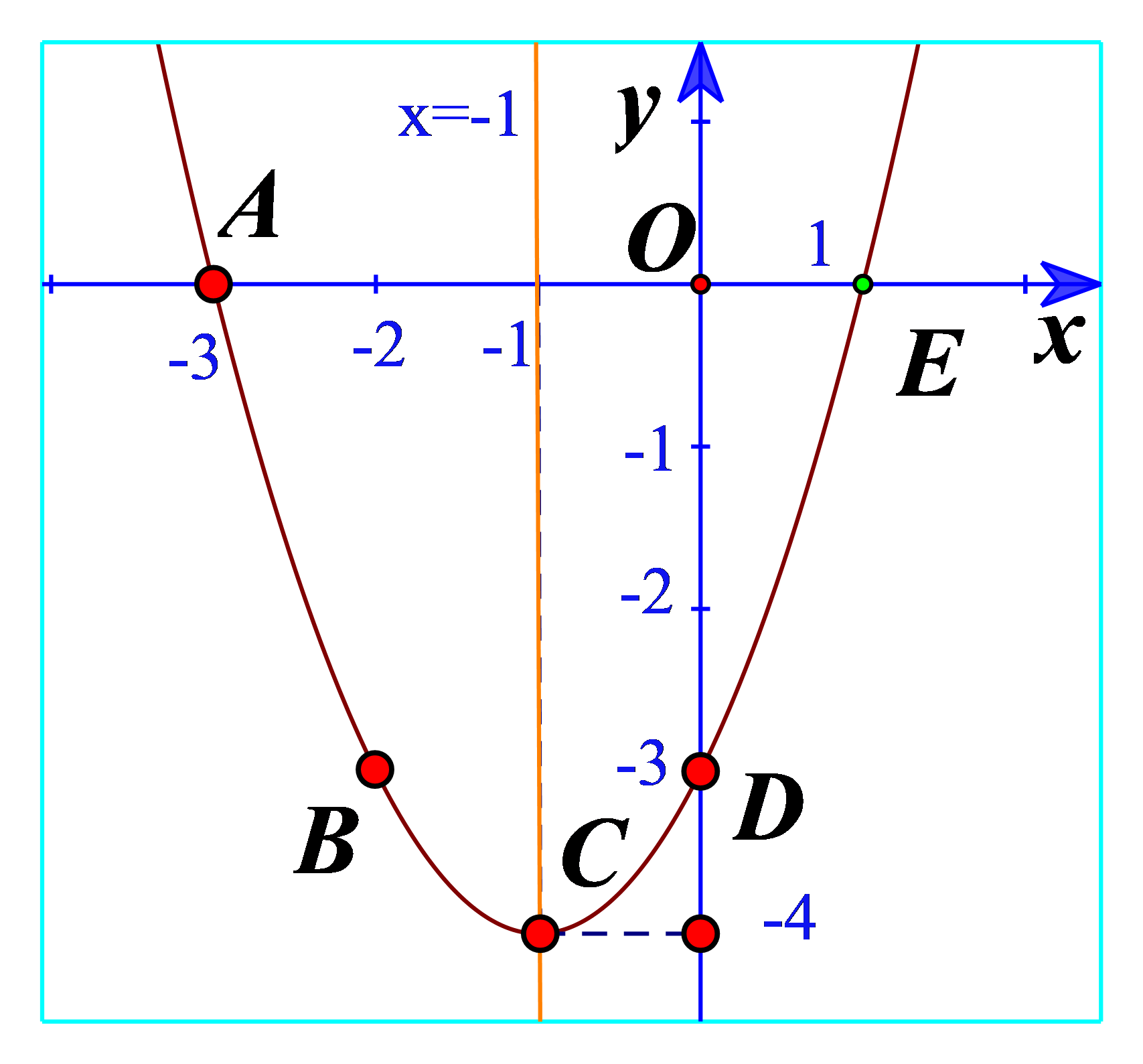
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Thay \(x = - 3,x = - 2,x = - 1,\)\(x = 0,x = 1\) vào hàm số.
b) Xác định các điểm trên mặt phẳng.
c) Sử dụng thước hoặc công cụ khác để vẽ đồ thị nối 5 điểm.
d) Tìm điểm thấp nhất trên hình vẽ và đường thẳng x=a với a là hoành độ của điểm thấp nhất.
Lời giải chi tiết:
a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
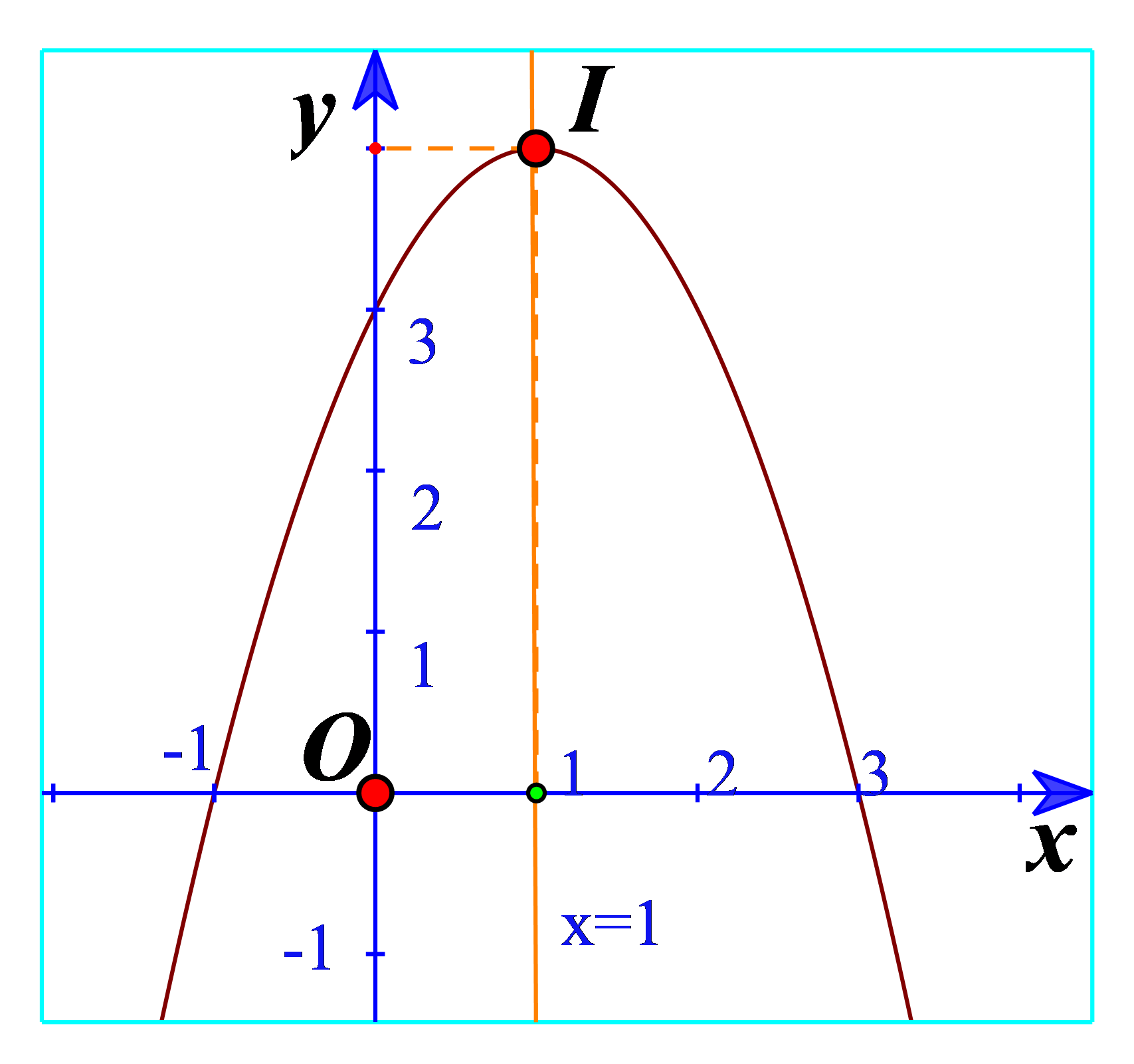
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
Phương pháp giải:
- Khoảng đồng biến: Khoảng mà đồ thị đi lên.
- Khoảng nghịch biến: Khoảng mà đồ thị đi xuống.
- Lập bảng biến thiên.
Lời giải chi tiết:
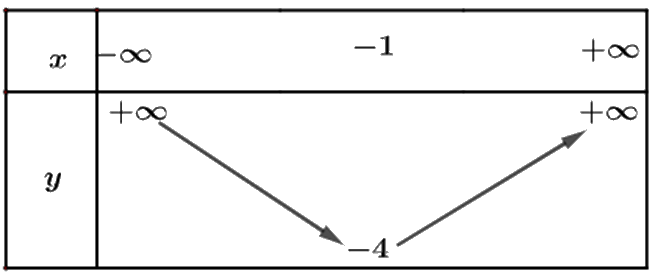
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
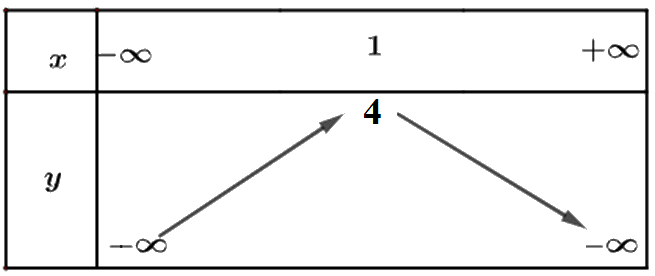
Vẽ đồ thị mỗi hàm số bậc hai sau:
a) \(y = {x^2} - 4x - 3\)
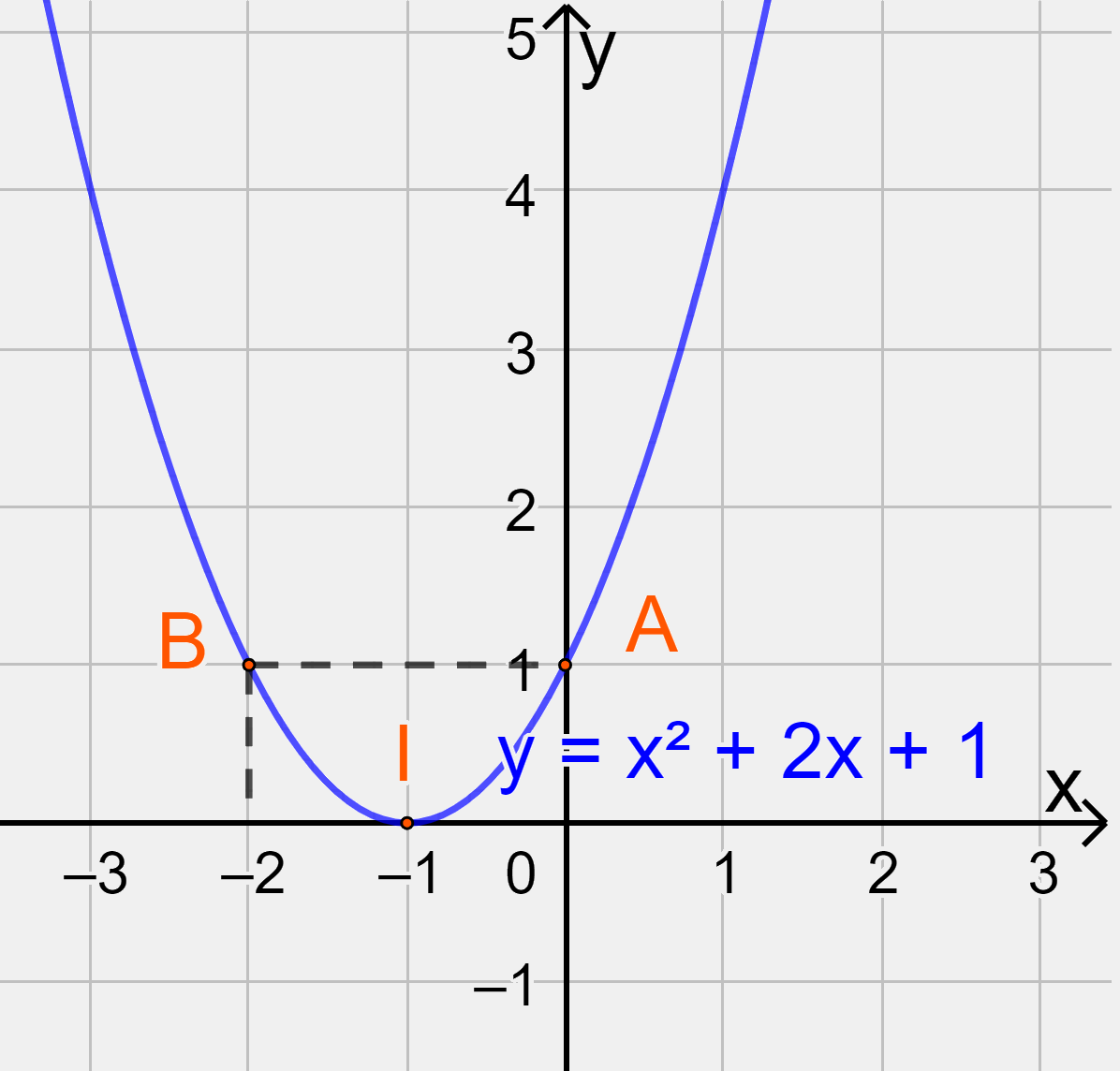
b) \(y = {x^2} + 2x + 1\)
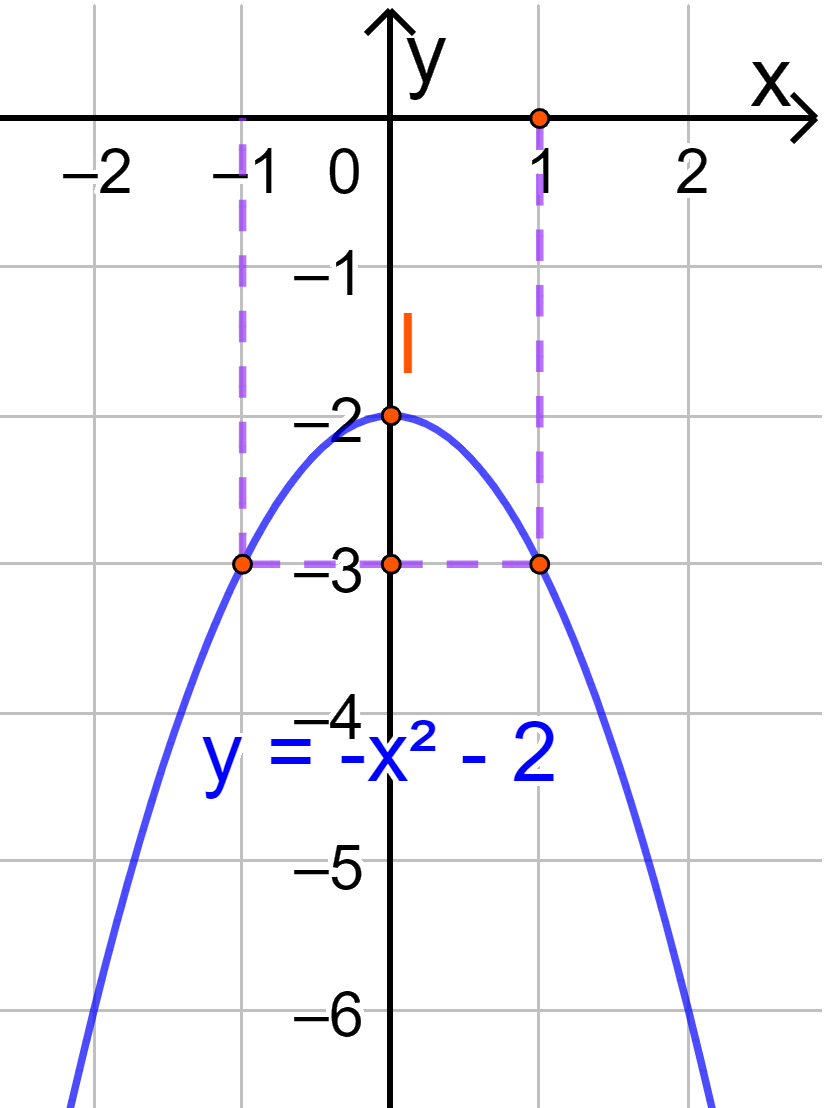
c) \(y = - {x^2} - 2\)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\)
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục \(x = - \frac{b}{{2a}}\).
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số \(y = a{x^2} + bx + c\).
Lời giải chi tiết:
a) Đồ thị hàm số có đỉnh \(I\left( {2; - 7} \right)\)
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
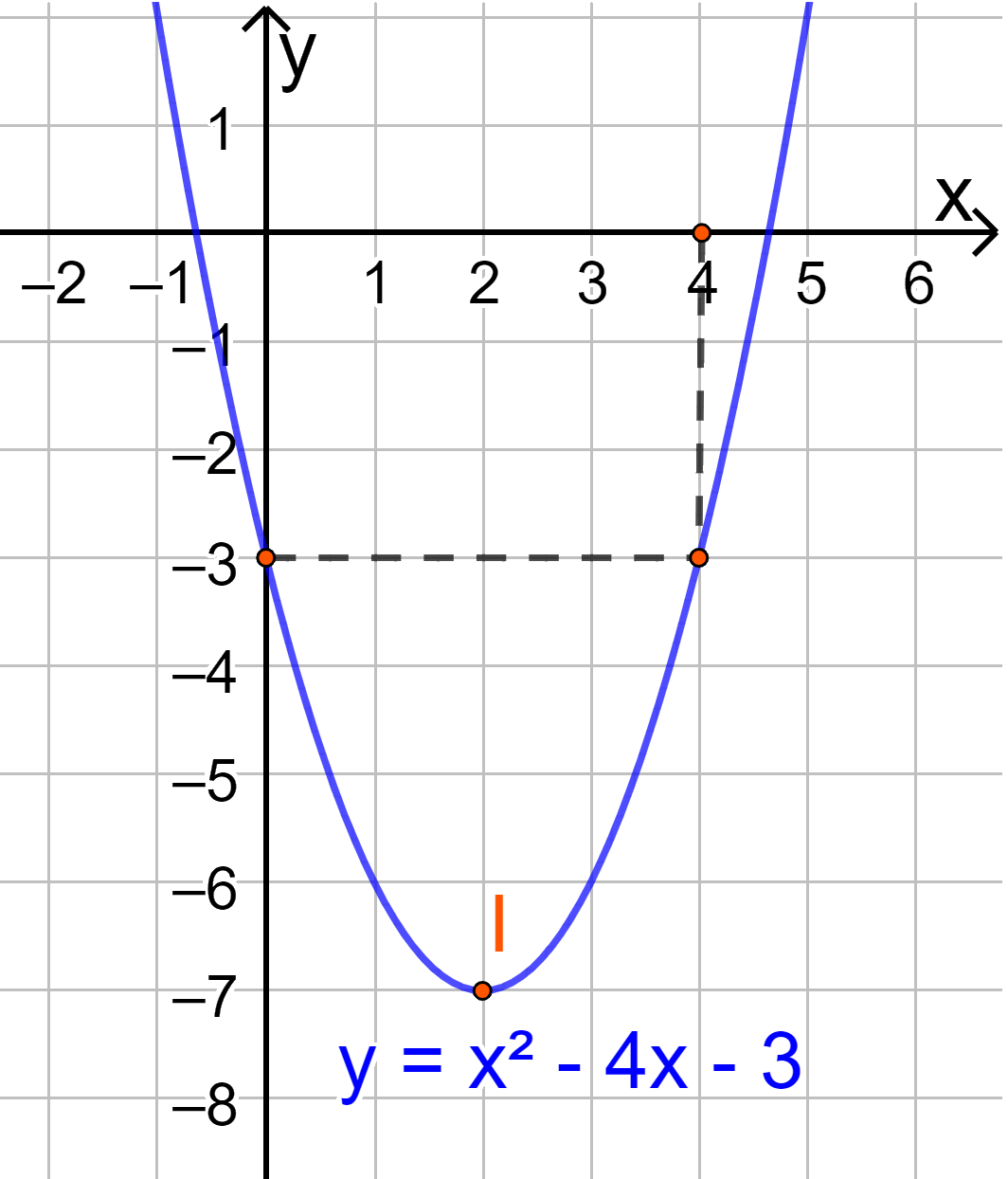
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
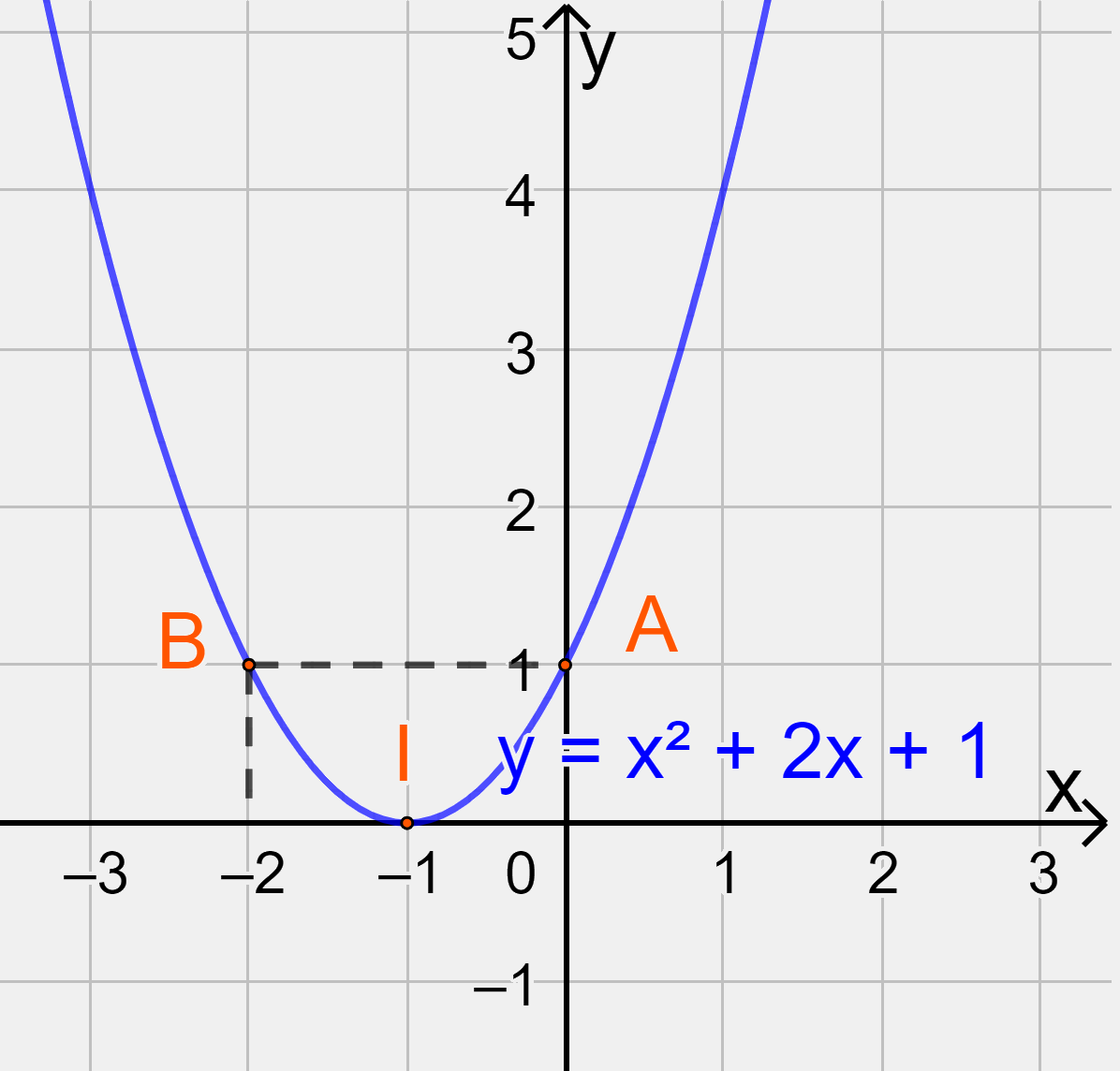
c) Đồ thị hàm số có đỉnh \(I\left( {0; - 2} \right)\)
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
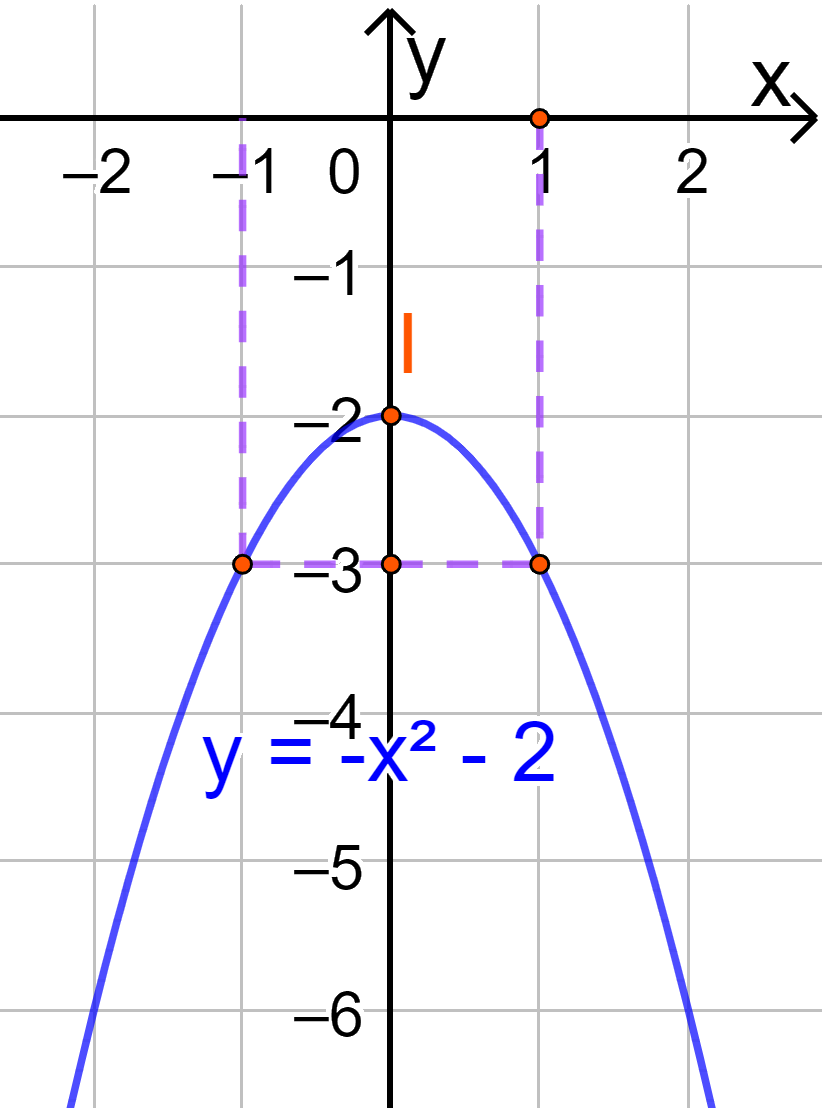
Cho hàm số \(y = - {x^2} + 2x + 3\).
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là \( - 1,0,1,2,3\) rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số \(y = - {x^2} + 2x + 3\) (Hình 12).
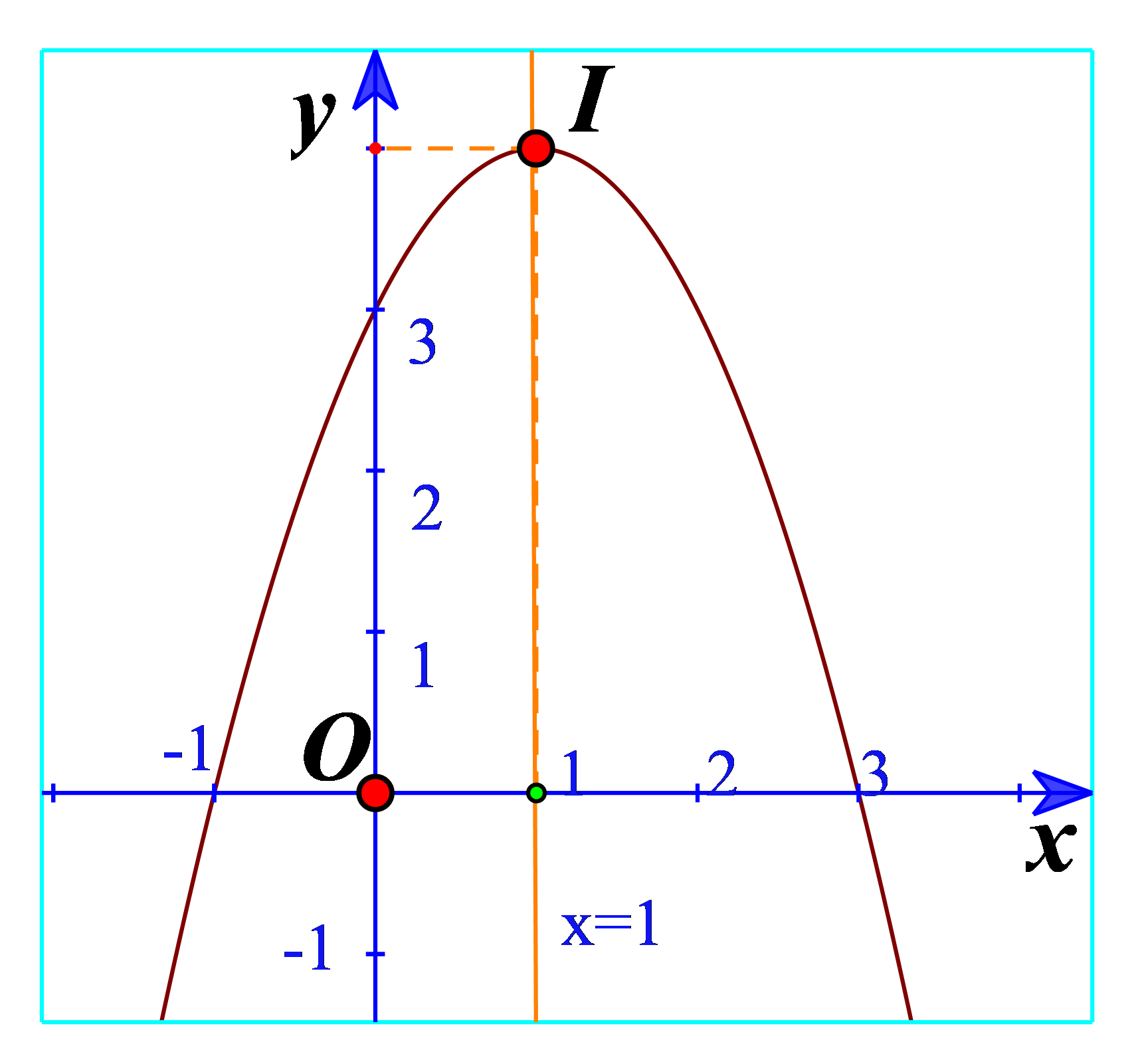
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Lần lượt thay \( - 1,0,1,2,3\) vào biểu thức của hàm số để tìm tung độ => Biểu diễn các điểm trên mặt phẳng tọa độ
b) Vẽ đường cong đi qua 5 điểm trên.
c) Tìm tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol. Xác định bề lõm.
Lời giải chi tiết:
a) x=-1 => y=0
x=0 => y=3
x=1=> y= 4
x=2 => y=3
x=3 => y=0
lần lượt là: A(-1;0), B(0;3), I(1;4), C(2;3), D(3;0)
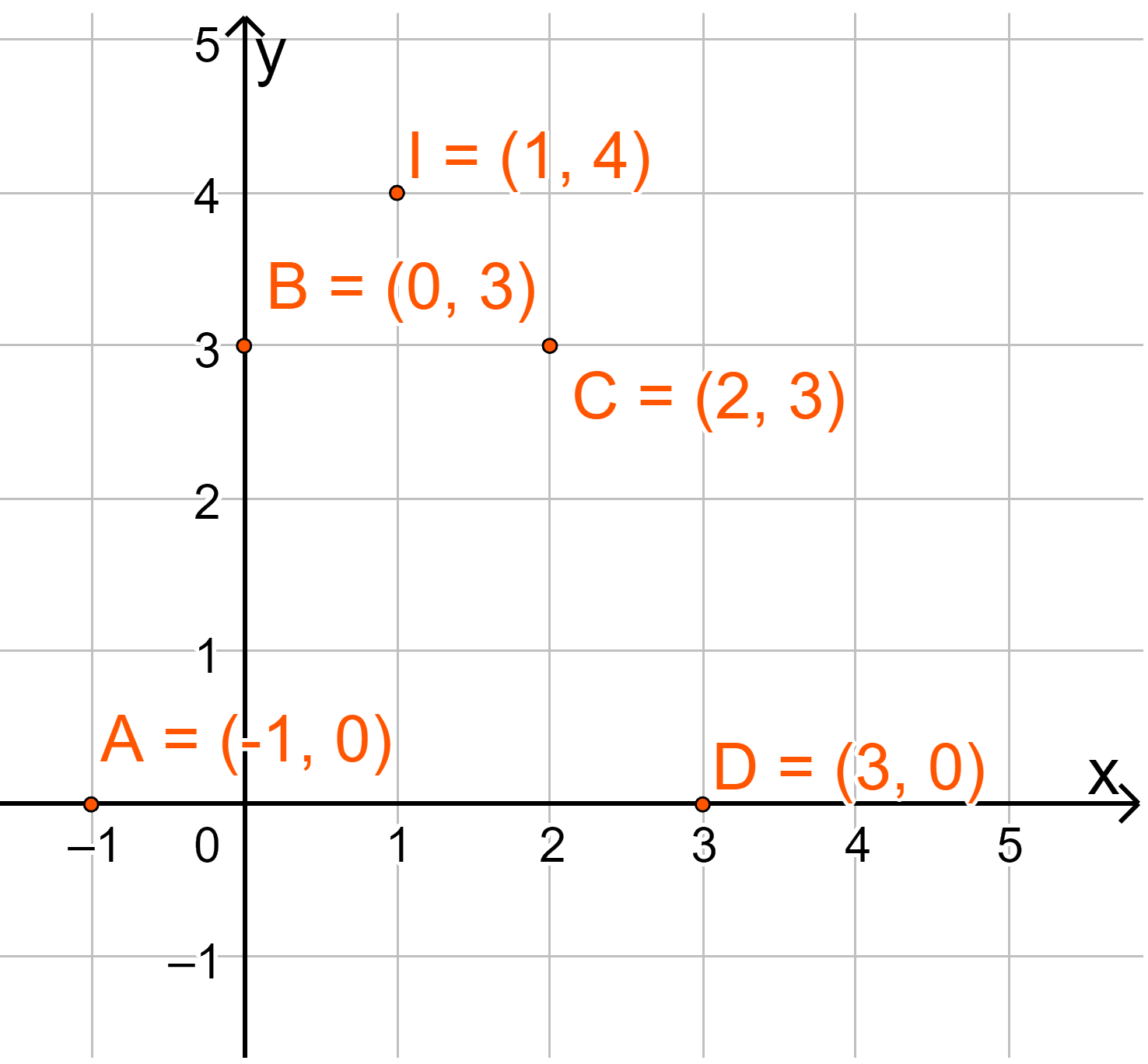
b) Vẽ đồ thị:
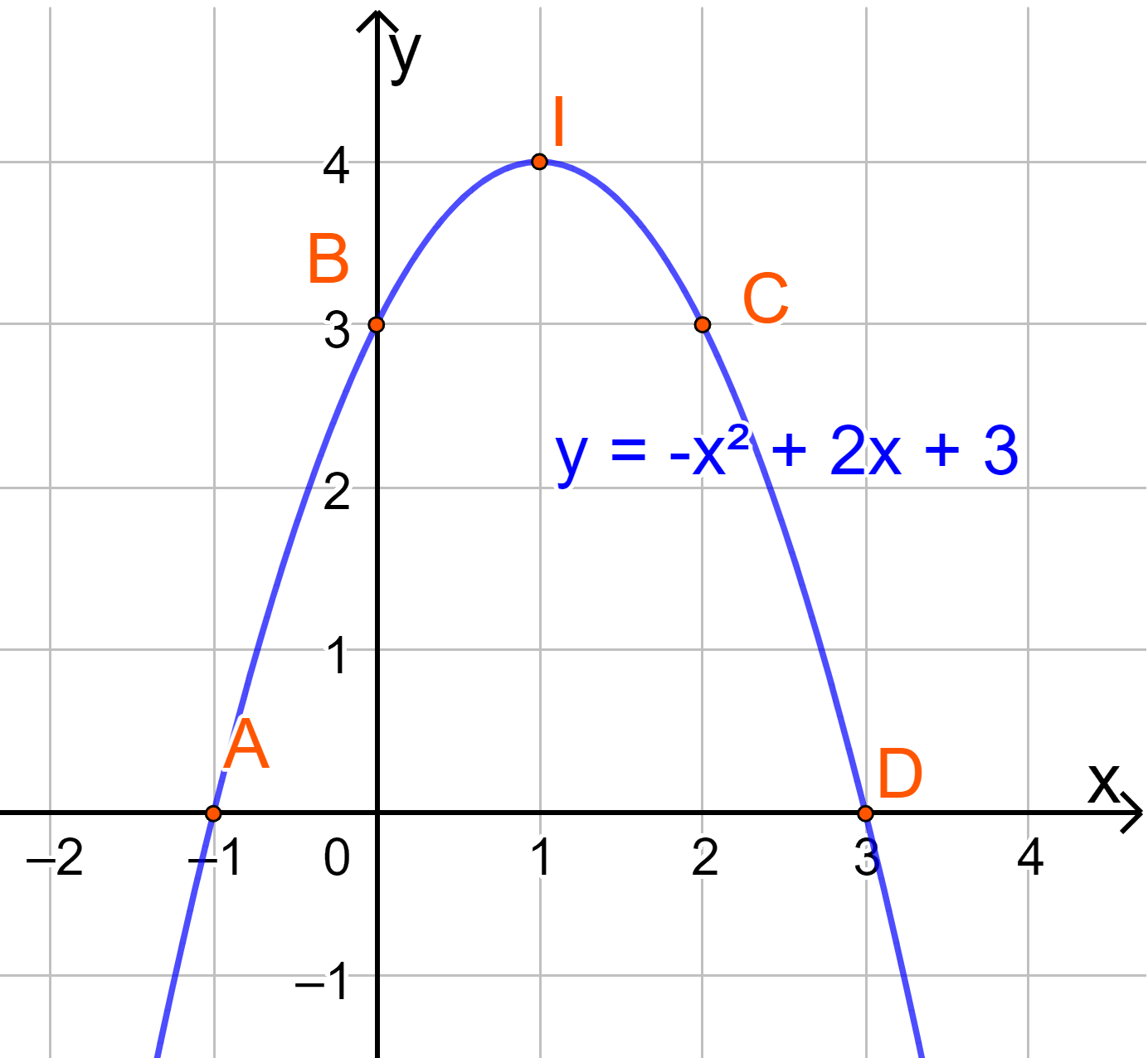
c) Điểm cao nhất là điểm I(1;4)
Phương trình trục đối xứng là đường thẳng x=1.
Đồ thị hàm số đó quay bề lõm xuống dưới.
Cho hàm số \(y = {x^2} + 2x - 3\).
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy.
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11).
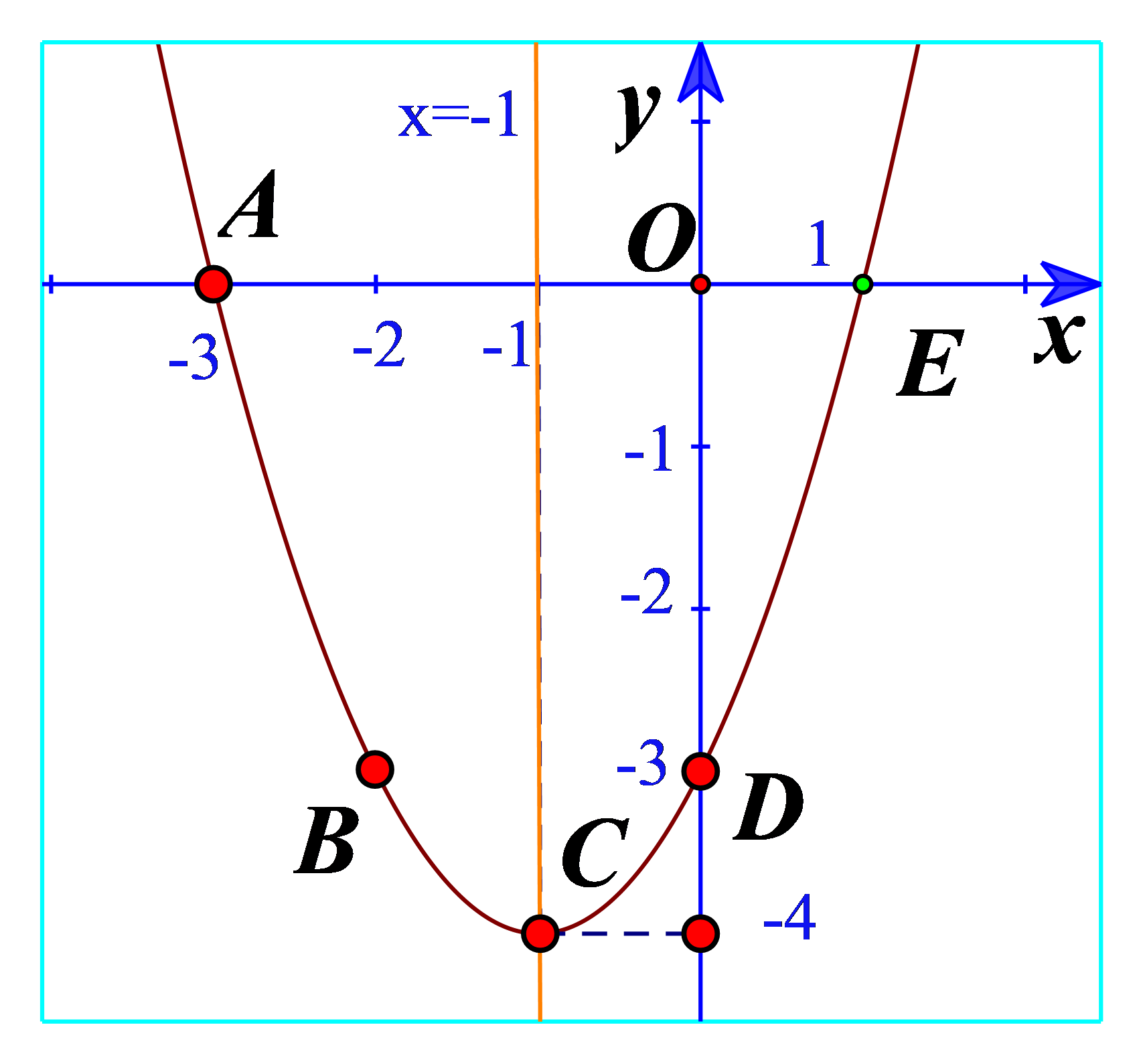
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Thay \(x = - 3,x = - 2,x = - 1,\)\(x = 0,x = 1\) vào hàm số.
b) Xác định các điểm trên mặt phẳng.
c) Sử dụng thước hoặc công cụ khác để vẽ đồ thị nối 5 điểm.
d) Tìm điểm thấp nhất trên hình vẽ và đường thẳng x=a với a là hoành độ của điểm thấp nhất.
Lời giải chi tiết:
a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
Cho hàm số \(y = - {x^2} + 2x + 3\).
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là \( - 1,0,1,2,3\) rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số \(y = - {x^2} + 2x + 3\) (Hình 12).
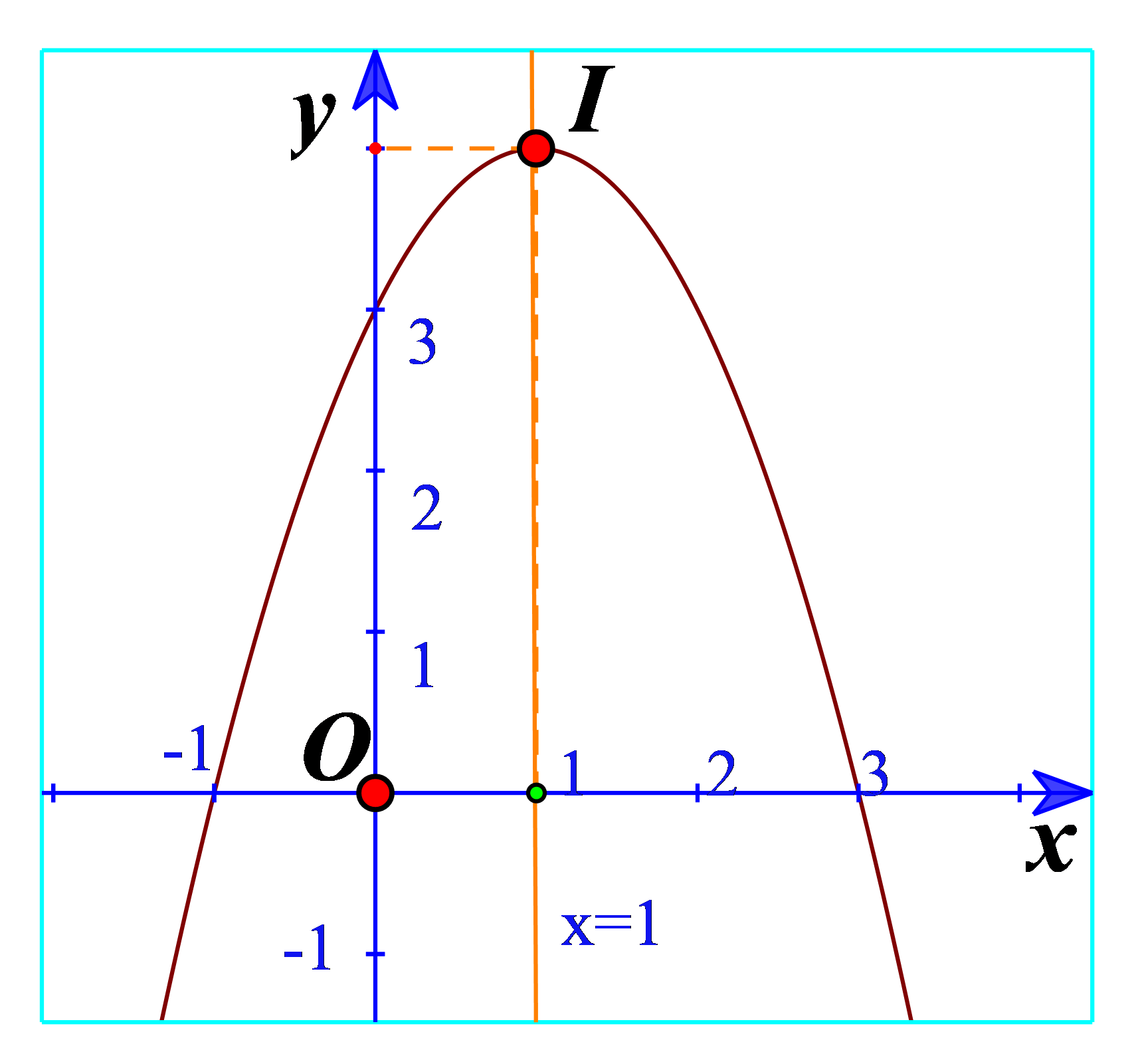
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Lần lượt thay \( - 1,0,1,2,3\) vào biểu thức của hàm số để tìm tung độ => Biểu diễn các điểm trên mặt phẳng tọa độ
b) Vẽ đường cong đi qua 5 điểm trên.
c) Tìm tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol. Xác định bề lõm.
Lời giải chi tiết:
a) x=-1 => y=0
x=0 => y=3
x=1=> y= 4
x=2 => y=3
x=3 => y=0
lần lượt là: A(-1;0), B(0;3), I(1;4), C(2;3), D(3;0)
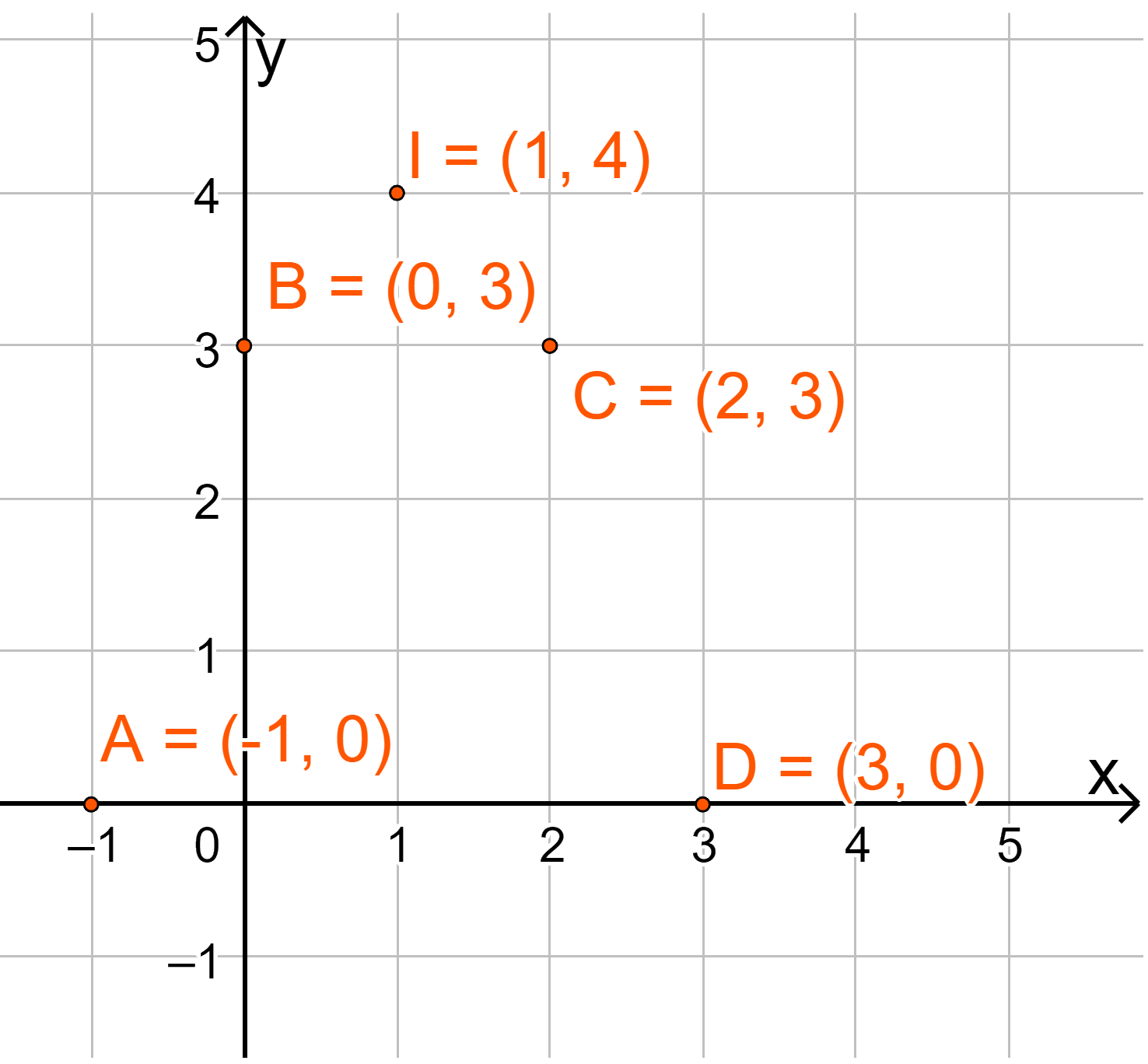
b) Vẽ đồ thị:
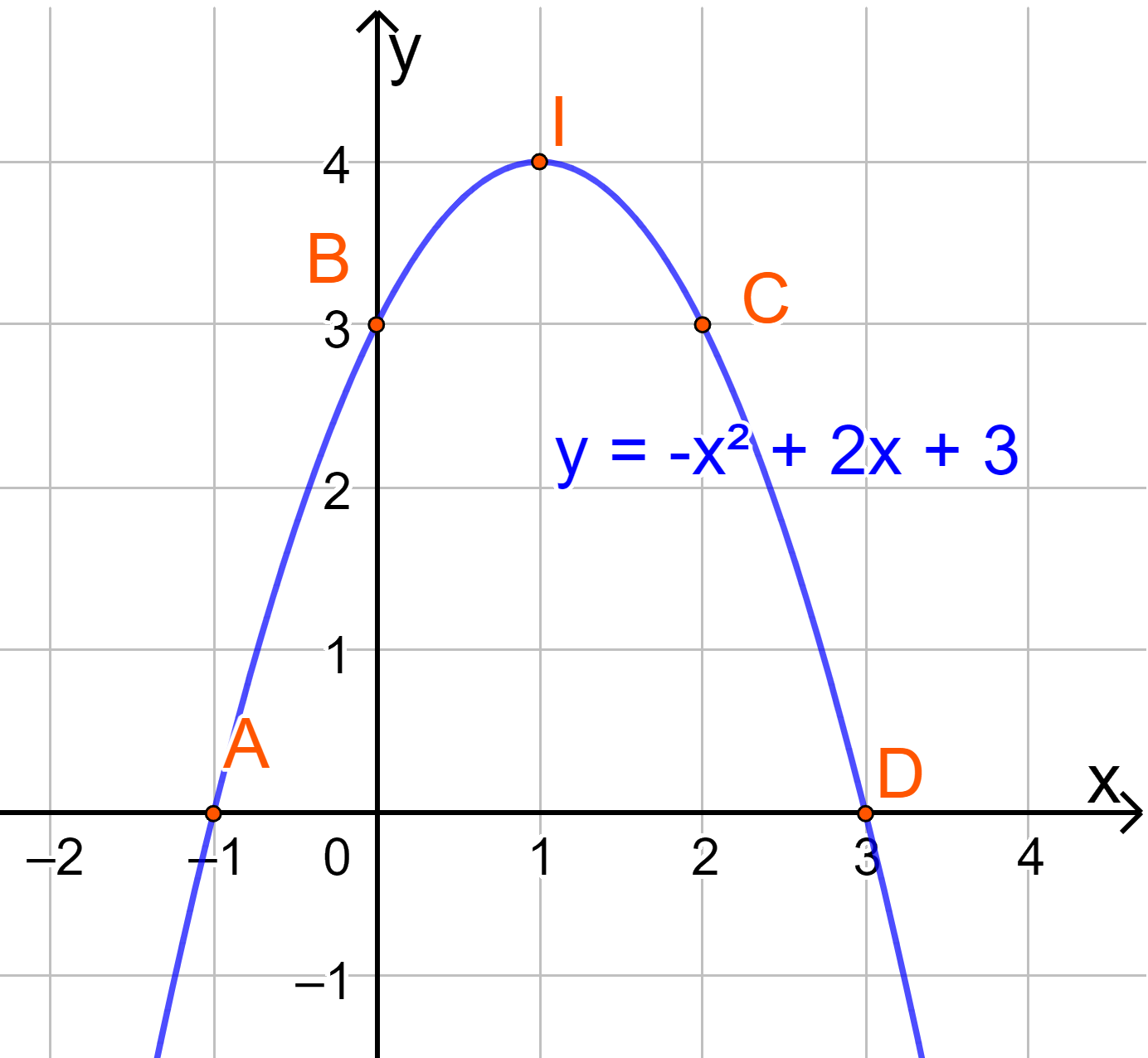
c) Điểm cao nhất là điểm I(1;4)
Phương trình trục đối xứng là đường thẳng x=1.
Đồ thị hàm số đó quay bề lõm xuống dưới.
Vẽ đồ thị mỗi hàm số bậc hai sau:
a) \(y = {x^2} - 4x - 3\)
b) \(y = {x^2} + 2x + 1\)
c) \(y = - {x^2} - 2\)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\)
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục \(x = - \frac{b}{{2a}}\).
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số \(y = a{x^2} + bx + c\).
Lời giải chi tiết:
a) Đồ thị hàm số có đỉnh \(I\left( {2; - 7} \right)\)
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
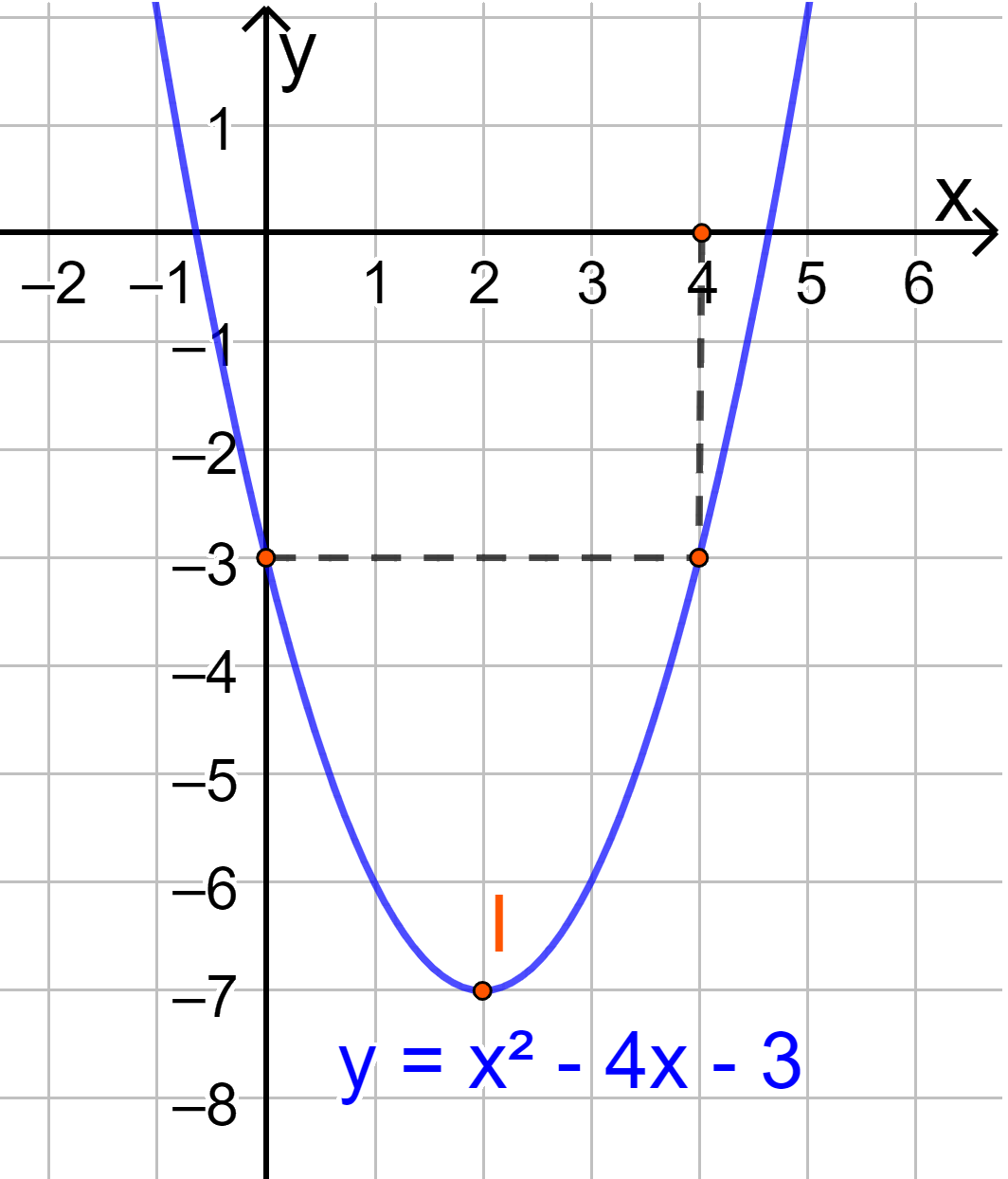
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
c) Đồ thị hàm số có đỉnh \(I\left( {0; - 2} \right)\)
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
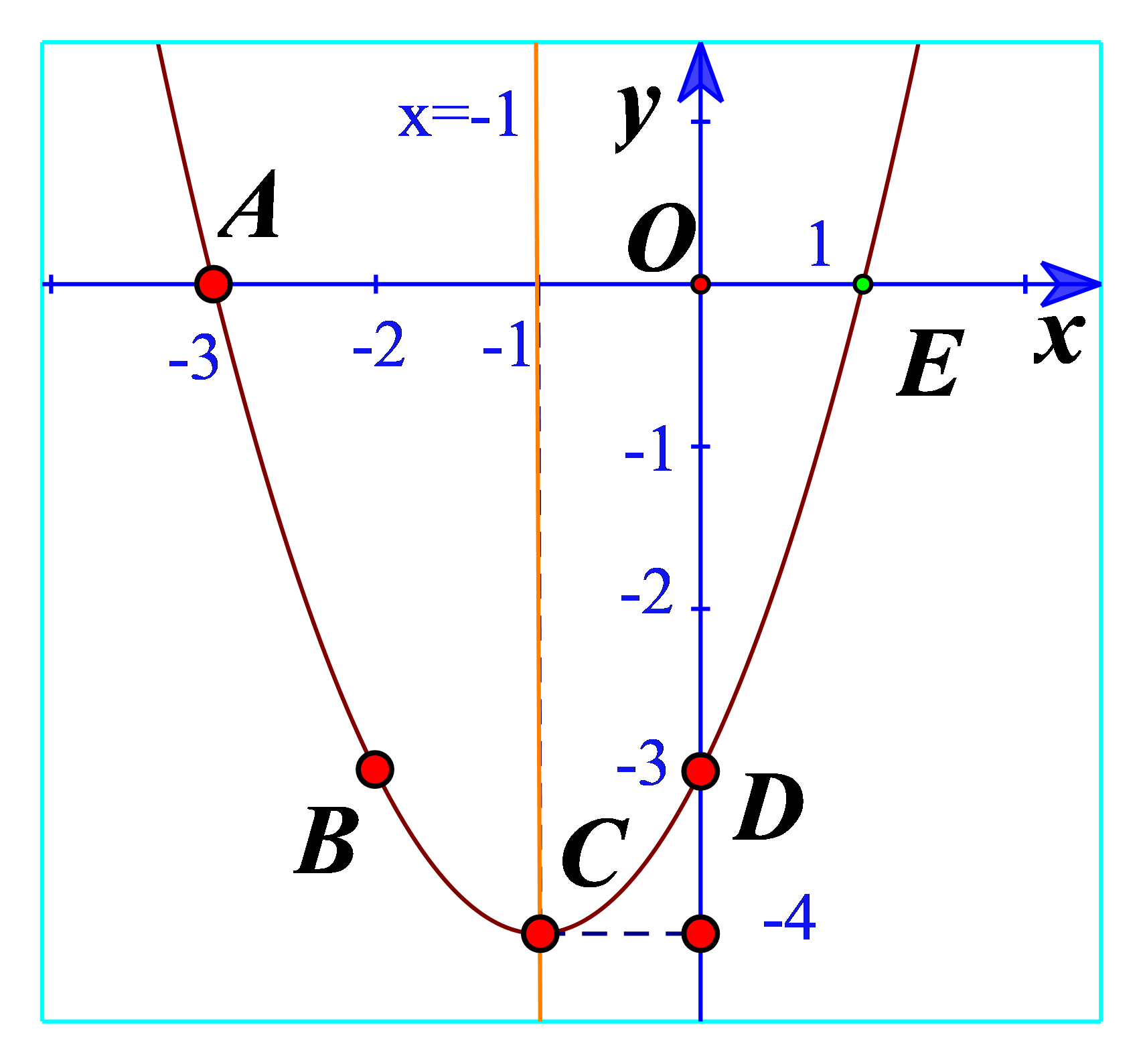
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
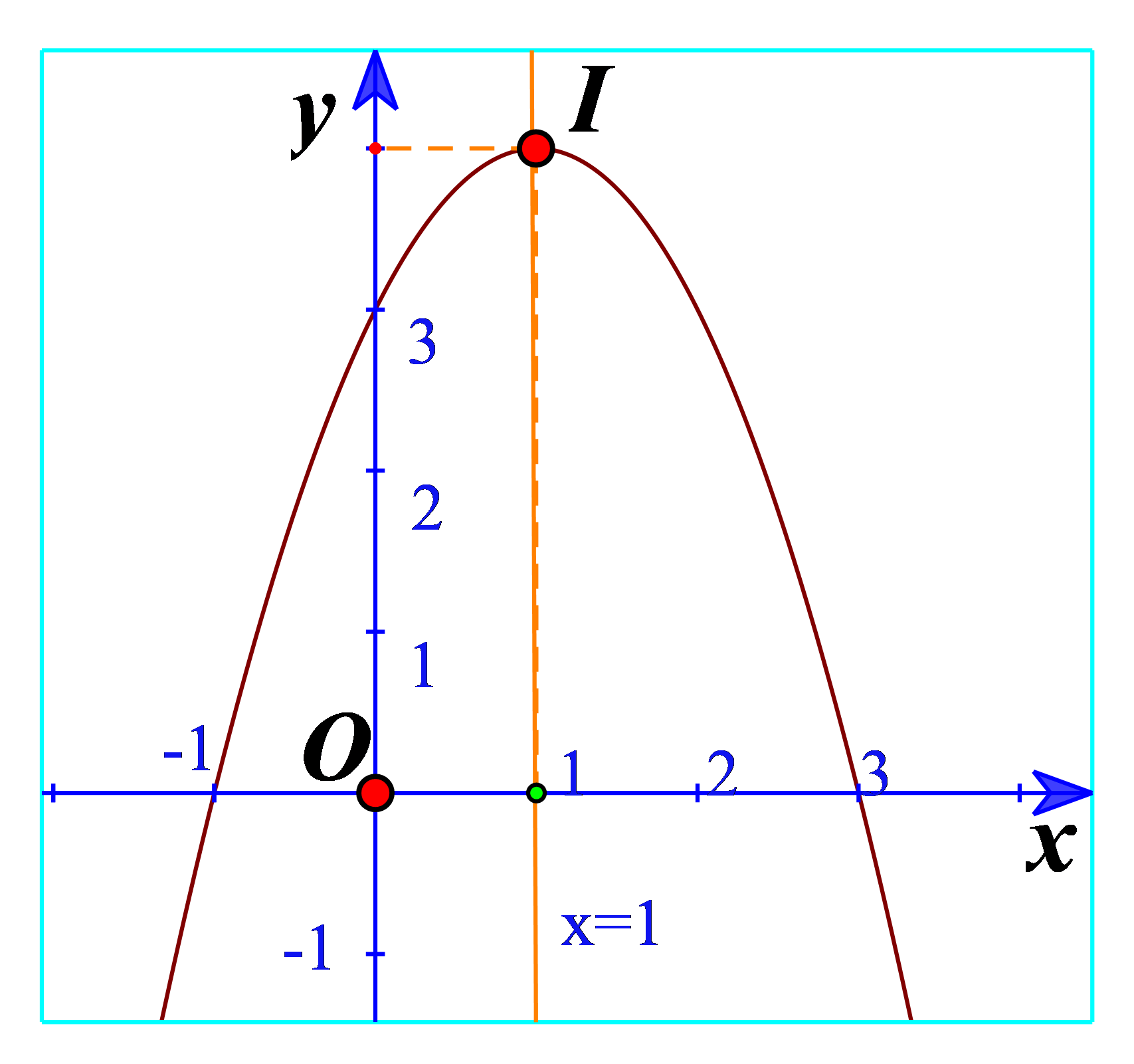
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
Phương pháp giải:
- Khoảng đồng biến: Khoảng mà đồ thị đi lên.
- Khoảng nghịch biến: Khoảng mà đồ thị đi xuống.
- Lập bảng biến thiên.
Lời giải chi tiết:
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
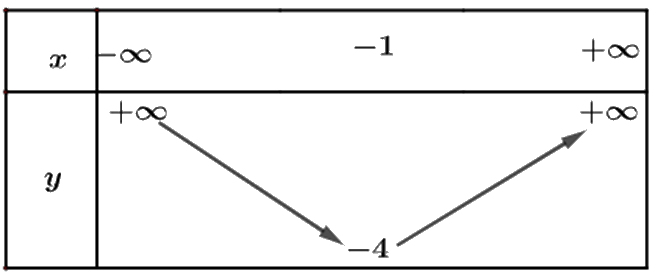
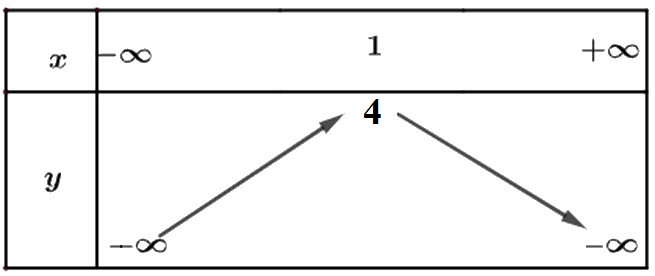
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
Lập bảng biến thiên của mỗi hàm số sau:
a) \(y = {x^2} - 3x + 4\)
b) \(y = - 2{x^2} + 5\)
Phương pháp giải:
- Xác định hệ số a, b.
- Tính \( - \frac{b}{{2a}}\).
- Tìm khoảng đồng biến, nghịch biến.
Lời giải chi tiết:
a) Hệ số \(a = 1 > 0,b = - 3 \Rightarrow \frac{{ - b}}{{2a}} = \frac{3}{2}\)
Vậy hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{3}{2}} \right)\) và đồng biến trên \(\left( {\frac{3}{2}; + \infty } \right)\)
b) Ta có \(a = - 2 < 0,b = 0\)
\( \Rightarrow - \frac{b}{{2a}} = 0\)
Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Mục II trong SGK Toán 10 tập 1 - Cánh diều là nền tảng quan trọng cho việc học tập các kiến thức toán học nâng cao hơn. Nó bao gồm các nội dung chính như tập hợp, các phép toán trên tập hợp, số thực, các tính chất của số thực, và các ứng dụng của số thực trong giải toán. Việc nắm vững các khái niệm và kỹ năng trong mục này sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả và chính xác.
Các bài tập trên trang 39 tập trung vào việc xác định các tập hợp, tìm các phần tử thuộc tập hợp, và thực hiện các phép toán cơ bản trên tập hợp như hợp, giao, hiệu, và phần bù. Để giải các bài tập này, học sinh cần nắm vững định nghĩa của tập hợp, các ký hiệu liên quan, và các quy tắc thực hiện các phép toán trên tập hợp.
Trang 40 giới thiệu các khái niệm về số thực, bao gồm số hữu tỉ và số vô tỉ, và các tính chất của số thực như tính giao hoán, tính kết hợp, tính phân phối. Các bài tập trên trang này yêu cầu học sinh vận dụng các tính chất của số thực để thực hiện các phép toán và chứng minh các đẳng thức.
Giá trị tuyệt đối của một số thực là khoảng cách từ số đó đến số 0 trên trục số. Các bài tập trên trang 41 yêu cầu học sinh tính giá trị tuyệt đối của các số thực, giải các phương trình và bất phương trình chứa giá trị tuyệt đối, và chứng minh các bất đẳng thức liên quan đến giá trị tuyệt đối.
Trang 42 là phần tổng hợp các kiến thức đã học trong Mục II. Các bài tập trên trang này thường có tính ứng dụng cao và yêu cầu học sinh vận dụng linh hoạt các kiến thức và kỹ năng đã học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong Mục II SGK Toán 10 tập 1 - Cánh diều. Lời giải được trình bày một cách rõ ràng, logic, và có kèm theo các chú thích và giải thích cần thiết để giúp học sinh hiểu rõ phương pháp giải và các bước thực hiện.
Ví dụ, đối với bài tập 1 trang 39, chúng ta có thể giải như sau:
Tương tự, đối với các bài tập khác, chúng ta cũng cần xác định rõ các yếu tố đầu vào, áp dụng các công thức và quy tắc phù hợp, và thực hiện các phép toán một cách chính xác.
Ngoài SGK Toán 10 tập 1 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng:
Giaitoan.edu.vn hy vọng rằng với những hướng dẫn chi tiết và hữu ích này, các em học sinh sẽ tự tin hơn trong việc học tập và giải bài tập Toán 10. Chúc các em học tốt!