Bài học này thuộc chương trình Toán 10 Cánh diều, tập trung vào việc giới thiệu khái niệm về số gần đúng và sai số. Đây là một phần quan trọng trong việc ứng dụng toán học vào thực tế, nơi mà việc biểu diễn chính xác tuyệt đối không phải lúc nào cũng khả thi.
Chúng ta sẽ cùng tìm hiểu cách xác định sai số tuyệt đối, sai số tương đối và cách sử dụng chúng để đánh giá độ chính xác của các phép tính và kết quả đo đạc.
A. Lý thuyết 1. Số gần đúng
A. Lý thuyết
1. Số gần đúng
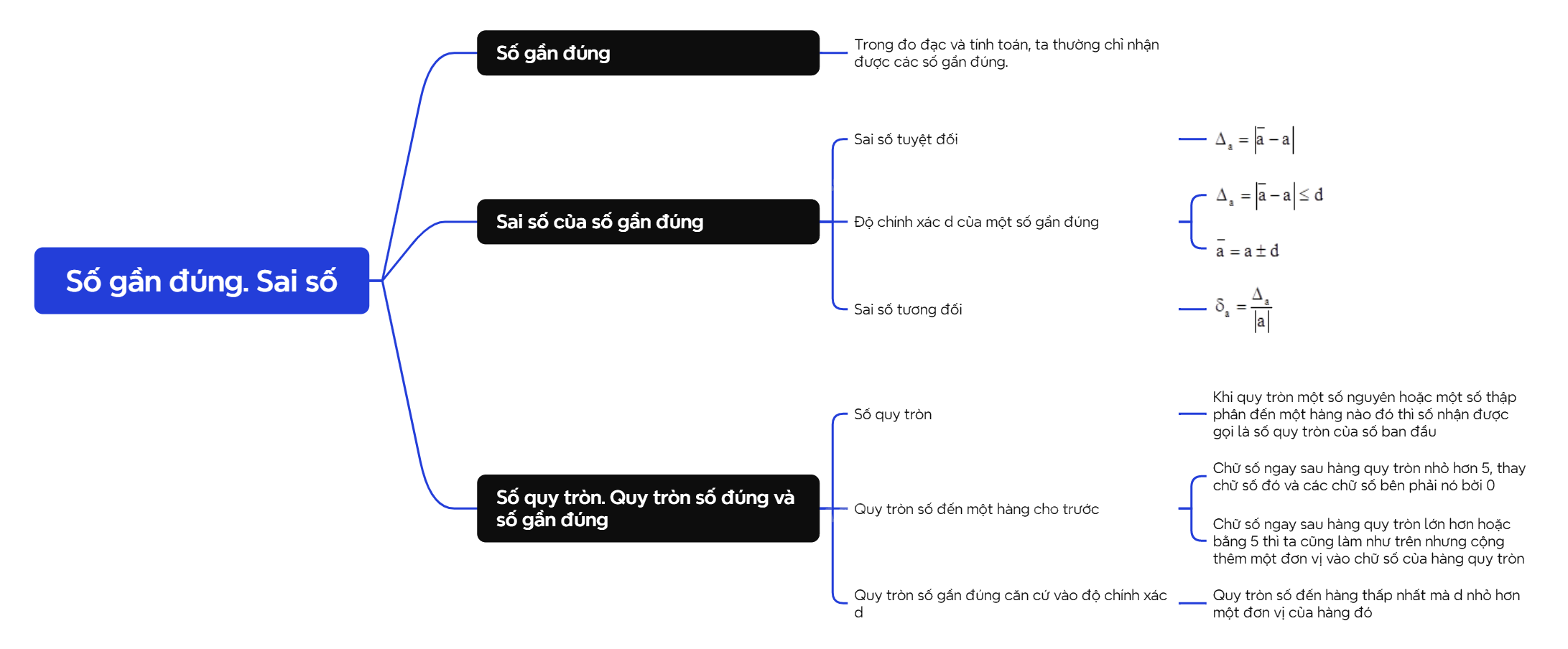
| Trong đo đạc và tính toán, ta thường chỉ nhận được các số gần đúng. |
2. Sai số của số gần đúng
a) Sai số tuyệt đối
| Nếu a là số gần đúng của số đúng \(\overline a \) thì \({\Delta _a} = \left| {\overline a - a} \right|\) được gọi là sai số tuyệt đối của số gần đúng a. |
Chú ý: Sai số tuyệt đối của số gần đúng nhận được trong một phép đo đạc, tính toán càng bé thì kết quả của phép đo đạc, tính toán đó càng chính xác.
b) Độ chính xác của một số gần đúng
| Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác d nếu \({\Delta _a} = \left| {\overline a - a} \right| \le d\) và quy ước viết gọn là \(\overline a = a \pm d\). |
Nhận xét: Nếu \({\Delta _a} \le d\) thì số đúng \(\overline a \) nằm trong đoạn [a – d; a + d] . Bởi vậy, d càng nhỏ thì độ sai lệch của số gần đúng a so với số đúng \(\overline a \) càng ít. Điều đó giải thích vì sao d được gọi là độ chính xác của số gần đúng.
c) Sai số tương đối
| Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số gần đúng a. |
Nhận xét:
- Nếu \(\overline a = a \pm d\) thì \({\Delta _a} \le d\). Do đó \({\delta _a} \le \frac{d}{{\left| a \right|}}\). Vì vậy, nếu \(\frac{d}{{\left| a \right|}}\) càng bé thì chất lượng của phép đo đạc, tính toán càng cao.
- Người ta thường viết sai số tương đối dưới dạng phần trăm.
3. Số quy tròn. Quy tròn số đúng và số gần đúng
a) Số quy tròn
| Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu. |
b) Quy tròn số đến một hàng cho trước
| Nêu lại quy tắc quy tròn số nguyên hoặc số thập phân đến một hàng cho trước: - Nếu chữ số ngay sau hàng quy tròn nhỏ hơn 5 thì ta chỉ việc thay chữ số đó và các chữ số bên phải nó bời 0. - Nếu chữ số ngay sau hàng quy tròn lớn hơn hoặc bằng 5 thì ta cũng làm như trên nhưng cộng thêm một đơn vị vào chữ số của hàng quy tròn. |
Nhận xét: Khi quy tròn số nguyên hoặc số thập phân đến một hàng cho trước thì sai số tuyệt đối của số quy tròn không vượt quá một phần đơn vị của hàng quy tròn. Như vậy, ta có thể lấy độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn.
c) Quy tròn số gần đúng căn cứ vào độ chính xác cho trước
| Cho a là số gần đúng với độ chính xác d. Giả sử a là số nguyên hoặc số thập phân. Khi được yêu cầu quy tròn số a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn số a đến hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó. |
B. Bài tập
Bài 1: Một bồn hoa có dạng hình tròn với bán kính là 0,8 m. Hai bạn Ngân và Ánh cùng muốn tính diện tích S của bồn hoa đó. Bạn Ngân lấy một giá trị gần đúng của \(\pi \) là 3,1 và được kết quả là \({S_1}\). Bạn Ánh lấy một giá trị gần đúng của \(\pi \) là 3,14 và được kết quả là \({S_2}\).
a) So sánh sai số tuyệt đối \({\Delta _{{S_1}}}\) của số gần đúng \({S_1}\) và sai số tuyệt đối \({\Delta _{{S_2}}}\) của số gần đúng \({S_2}\). Bạn nào cho kết quả chính xác hơn?
b) Ước lượng sai số tuyệt đối \({\Delta _{{S_1}}}\) và \({\Delta _{{S_1}}}\).
Giải:
a) Ta có: \({S_1} = 3,1.0,{8^2} = 1,984\) \(({m^2})\); \({S_2} = 3,14.0,{8^2} = 2,0096\) \(({m^2})\).
Ta thấy: \(3,1 < 3,14 < \pi \) nên \(3,1.0,{8^2} < 3,14.0,{8^2} < \pi .0,{8^2}\), tức là \({S_1} < {S_2} < S\).
Suy ra \({\Delta _{{S_2}}} = \left| {S - {S_2}} \right| < \left| {S - {S_1}} \right| = {\Delta _{{S_1}}}\).
Vậy bạn Ánh cho kết quả chính xác hơn.
b) Do \(3,1 < \pi < 3,15\) nên \(3,1.0,{8^2} < \pi .0,{8^2} < 3,15.0,{8^2}\). Suy ra \(1,984 < S < 2,016\).
Vậy \({\Delta _{{S_1}}} = \left| {S - {S_1}} \right| < 2,016 - 1,984 = 0,032\).
Ta nói: Kết quả của bạn Ngân có sai số tuyệt đối không vượt quá 0,032 hay có độ chính xác là 0,032.
Do \(3,14 < \pi < 3,15\) nên \(3,14.0,{8^2} < \pi .0,{8^2} < 3,15.0,{8^2}\). Suy ra \(1,984 < S < 2,016\).
Vậy \({\Delta _{{S_1}}} = \left| {S - {S_1}} \right| < 2,016 - 2,0096 = 0,0064\).
Ta nói: Kết quả của bạn Ánh có sai số tuyệt đối không vượt quá 0,0064 hay có độ chính xác là 0,0064.
Bài 2: Viết số quy tròn của mỗi số gần đúng sau:
a) Số gần đúng a = 1,941,247 với độ chính xác d = 300.
b) Số gần đúng a = 4,1463 với độ chính xác d = 0,0095.
Giải:
a) Do 100 < d = 300 < 1,000 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng nghìn. Vì thế, ta quy tròn a đến hàng nghìn theo quy tắc quy tròn đã nêu ở trên. Vậy số quy tròn của a là 1,941,000.
b) Do 0,001 < d = 0,0095 < 0,01 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng phần trăm. Vì thế, ta quy tròn số a đến hàng phần trăm theo quy tắc quy tròn đã nêu ở trên. Vậy số quy tròn của a là 4,15.
Bài 3: Một tờ giấy A4 có dạng hình chữ nhật với chiều dài, chiều rộng lần lượt là 29,7 cm và 21 cm. Tính độ dài đường chéo của tờ giấy A4 đó và xác định độ chính xác của kết quả tìm được.
Giải:
Gọi x là độ dài đường chéo của tờ giấy A4 đã cho. Theo định lý Pythagore, ta có:
\(x = \sqrt {29,{7^2} + {{21}^2}} = \sqrt {882,09 + 441} = \sqrt {1323,09} = 36,3743...\)
Nếu lấy giá trị gần đúng của x là 36,37 thì 36,37 < x < 36,375.
Suy ra | x – 36,37 | < 36,375 – 36,37 = 0,005.
Vậy độ dài đường chéo của tờ giấy A4 đã cho là \(x \approx 36,37\) và độ chính xác của kết quả tìm được là 0,005, hay nói cách khác \(x = 36,37 \pm 0,005\).
Trong khoa học và kỹ thuật, việc đo đạc và tính toán thường dẫn đến các kết quả không hoàn toàn chính xác. Điều này là do các yếu tố như giới hạn của dụng cụ đo, sai số của phương pháp tính toán, và các yếu tố ngẫu nhiên khác. Do đó, việc hiểu rõ về số gần đúng và sai số là vô cùng quan trọng.
Một số được gọi là số gần đúng nếu nó được sử dụng để thay thế cho một số chính xác, khi số chính xác đó không thể biết chính xác hoặc quá phức tạp để tính toán. Ví dụ, khi đo chiều dài của một vật thể bằng thước đo, chúng ta thường thu được một số gần đúng, vì thước đo chỉ có độ chính xác đến một giá trị nhất định.
Sai số tuyệt đối của một số gần đúng a so với số chính xác x được định nghĩa là:
|a - x|
Sai số tuyệt đối cho biết mức độ lệch giữa số gần đúng và số chính xác.
Sai số tương đối của một số gần đúng a so với số chính xác x (với x ≠ 0) được định nghĩa là:
| (a - x) / x |
Sai số tương đối cho biết mức độ lệch của số gần đúng so với số chính xác, được biểu diễn dưới dạng tỷ lệ phần trăm.
Khi thực hiện các phép tính với số gần đúng, sai số sẽ tích lũy và ảnh hưởng đến kết quả cuối cùng. Để ước lượng sai số trong các phép tính, chúng ta có thể sử dụng các quy tắc sau:
Ví dụ 1: Giả sử chiều dài của một đoạn thẳng là 10.5 cm, nhưng chúng ta đo được là 10.4 cm. Tính sai số tuyệt đối và sai số tương đối.
Sai số tuyệt đối: |10.4 - 10.5| = 0.1 cm
Sai số tương đối: |(10.4 - 10.5) / 10.5| ≈ 0.0095
Ví dụ 2: Tính giá trị của 2.3 + 3.7 với sai số tuyệt đối của mỗi số là 0.05. Ước lượng sai số của kết quả.
Sai số của kết quả: 0.05 + 0.05 = 0.1
Lý thuyết số gần đúng và sai số có nhiều ứng dụng trong thực tế, bao gồm:
Giải các bài tập trong SGK Toán 10 Cánh diều liên quan đến số gần đúng và sai số để củng cố kiến thức và rèn luyện kỹ năng.
Việc nắm vững lý thuyết số gần đúng và sai số là nền tảng quan trọng cho việc học tập và làm việc trong nhiều lĩnh vực khoa học và kỹ thuật. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về chủ đề này.