Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
Đề bài
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) \(x + 2y < 3\);
b) \(3x - 4y \ge - 3\);
c) \(y \ge - 2x + 4\);
d) \(y < 1 - 2x\).
Phương pháp giải - Xem chi tiết
Các bước biểu diễn miền nghiệm:
- Vẽ đường thẳng
- Thay tọa độ điểm O(0;0) vào bất phương trình
- Nếu thỏa mãn thì điểm O nằm trong miền nghiệm, ta gạch phần không chứa O
- Ngược lại thì không nằm trong miền nghiệm ta gạch phần chứa O.
Lời giải chi tiết
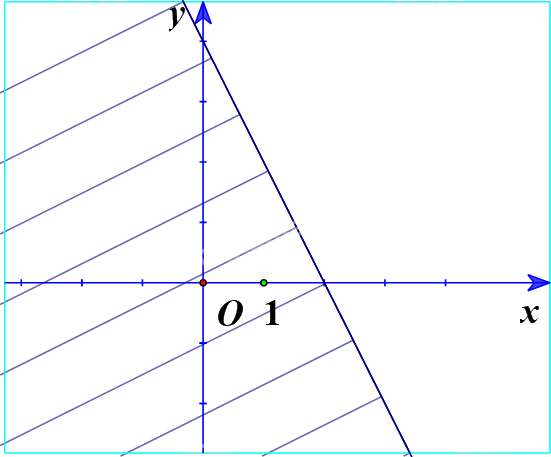
a) Ta vẽ đường thẳng d’:\(x + 2y = 3 \Leftrightarrow y = - \frac{x}{2} + \frac{3}{2}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(x + 2y < 3\) ta được:
\(0 + 2.0 = 0 < 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
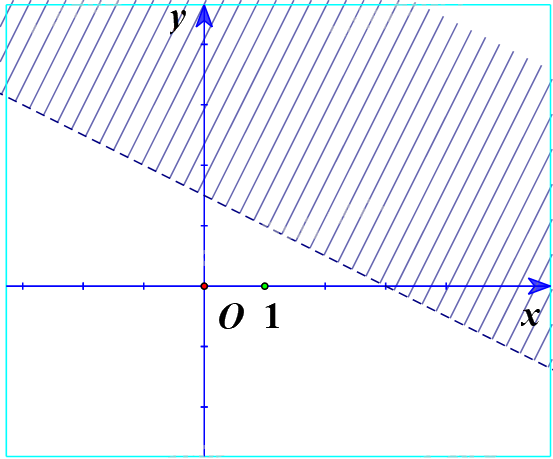
b) Ta vẽ đường thẳng d:\(3x - 4y = - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(3x - 4y \ge - 3\) ta được:
\(3.0 - 4.0 = 0 \ge - 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
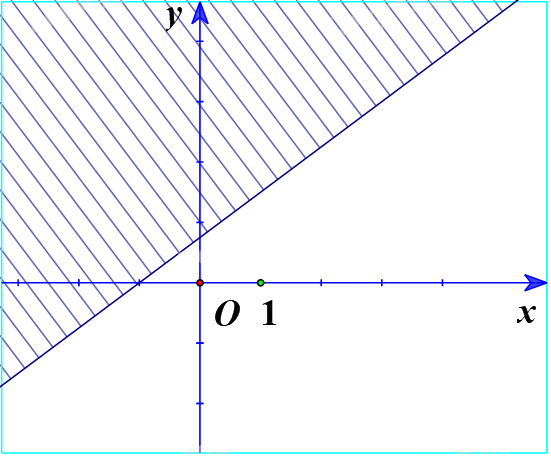
c) Ta vẽ đường thẳng d:\(y = - 2x + 4\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y \ge - 2x + 4\) ta được:
\(0 \ge - 2.0 + 4 \Leftrightarrow 0 \ge 4\) (Vô lí)
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm:
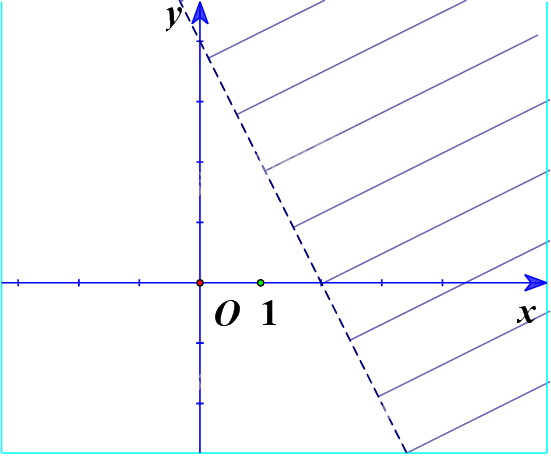
d) Ta vẽ đường thẳng d:\(y = 1 - 2x\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y < 1 - 2x\) ta được:
\(0 < 1 - 2.0\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
Chú ý
Đối với các bất phương trình có dấu “<” hoặc “>” thì vẽ đường thẳng là nét đứt.
Đối với các bất phương trình có dấu “\( \le \)” hoặc “\( \ge \)” thì vẽ đường thẳng là nét liền.
Bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp để giải quyết các bài toán cụ thể. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa, ký hiệu, và các quy tắc liên quan đến tập hợp.
Bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều một cách hiệu quả, học sinh cần:
Bài tập: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Tìm A ∪ B và A ∩ B.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, học sinh có thể luyện tập thêm các bài tập sau:
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về tập hợp:
Bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp học sinh nắm vững kiến thức cơ bản về tập hợp. Bằng cách nắm vững định nghĩa, quy tắc, và phương pháp giải bài tập, học sinh có thể tự tin giải quyết các bài toán liên quan đến tập hợp một cách hiệu quả.