Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 10 tập 1 - Cánh diều, đặc biệt là mục II trang 21, 22, 23, 24.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Cho bất phương trình 2x – y>2 (3). a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng d:2x - y = 2 => y = 2x - 2 Biểu diễn miền nghiệm của mỗi bất phương trình sau:
Cho bất phương trình 2x – y > 2 (3).
a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng \(d:2x - y = 2 \Leftrightarrow y = 2x - 2\).
b) Xét điểm M(2;-1). Chứng tỏ (2;-1) là nghiệm của bất phương trình (3).
c) Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2;- 1).
Phương pháp giải:
a) Vẽ đường thẳng y = 2x - 2 trên mặt phẳng tọa độ.
b) Thay tọa độ điểm M vào bất phương trình (3), nếu thỏa mãn thì (2;-1) là một nghiệm của bất phương trình (3).
c) Gạch phần không chứa điểm M.
Lời giải chi tiết:
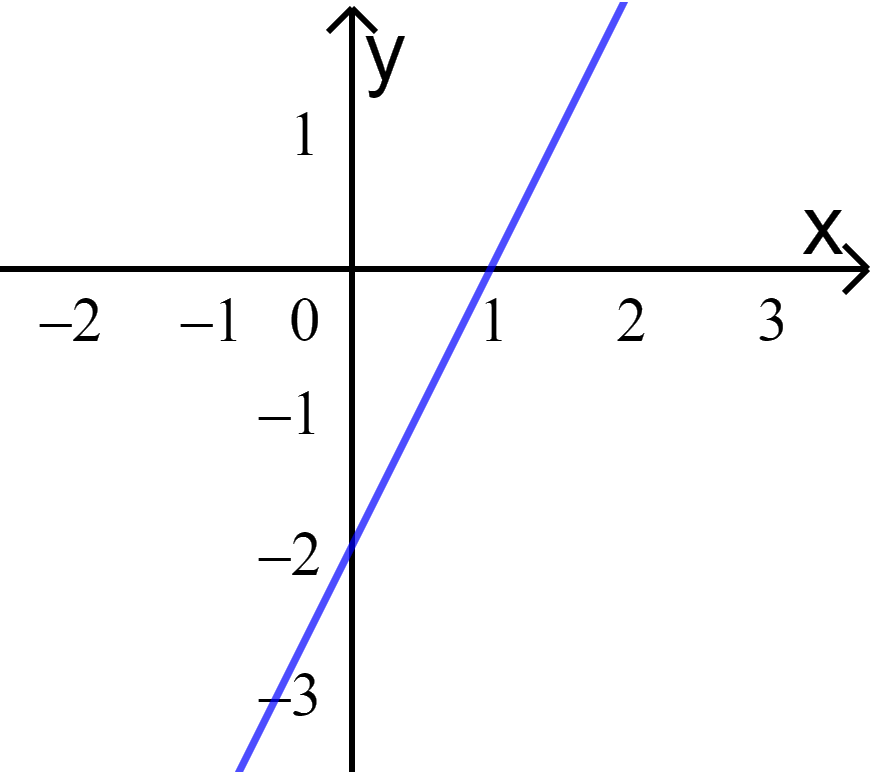
a) Cho x = 0 => y = -2.
Cho y = 0 => x = 1.
Nối hai điểm (0;-2) và (1;0) ta được:
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:
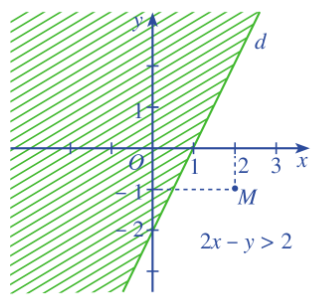
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) \(x - 2y < 4\)
b) \(x + 3y \ge 6\).
Phương pháp giải:
Các bước biểu diễn miền nghiệm:
- Vẽ đường thẳng.
- Thay tọa độ điểm O(0;0) vào bất phương trình.
- Nếu thỏa mãn thì điểm O nằm trong miền nghiệm, ta gạch phần không chứa O.
- Ngược lại thì không nằm trong miền nghiệm ta gạch phần chứa O.
Lời giải chi tiết:
a) Ta vẽ đường thẳng d:\(x - 2y = 4 \Leftrightarrow y = \frac{x}{2} - 2\).
Cho x = 0 thì y = –2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0;–2) và (4;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x - 2y < 4\) ta được:
\(0 - 2.0 < 4\) (Luôn đúng).
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
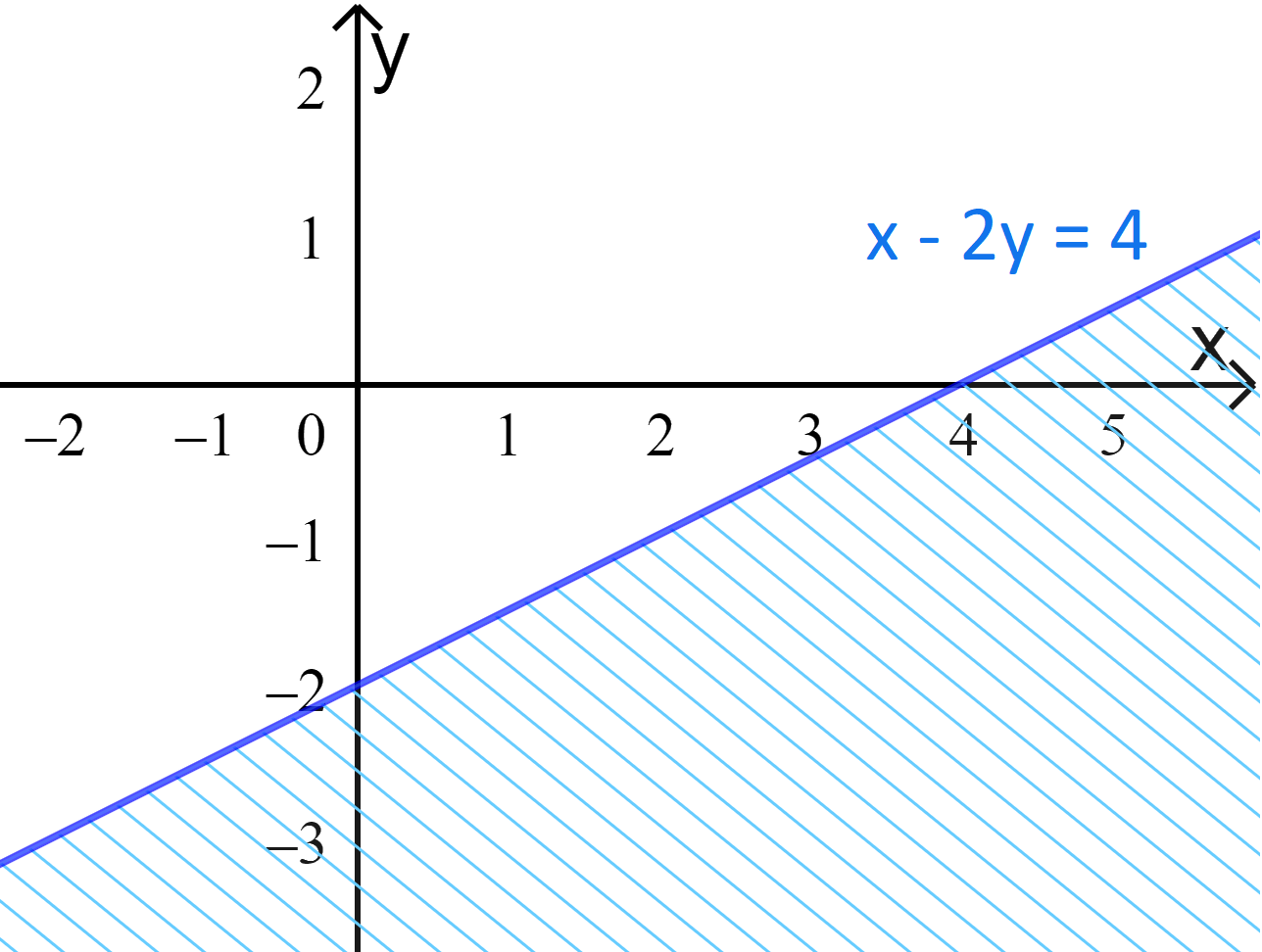
b) Ta vẽ đường thẳng d:\(x+3y=6 \).
Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0;2) và (6;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x+3y=6 \) ta được:
\(0+3.0 < 6\).
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm:
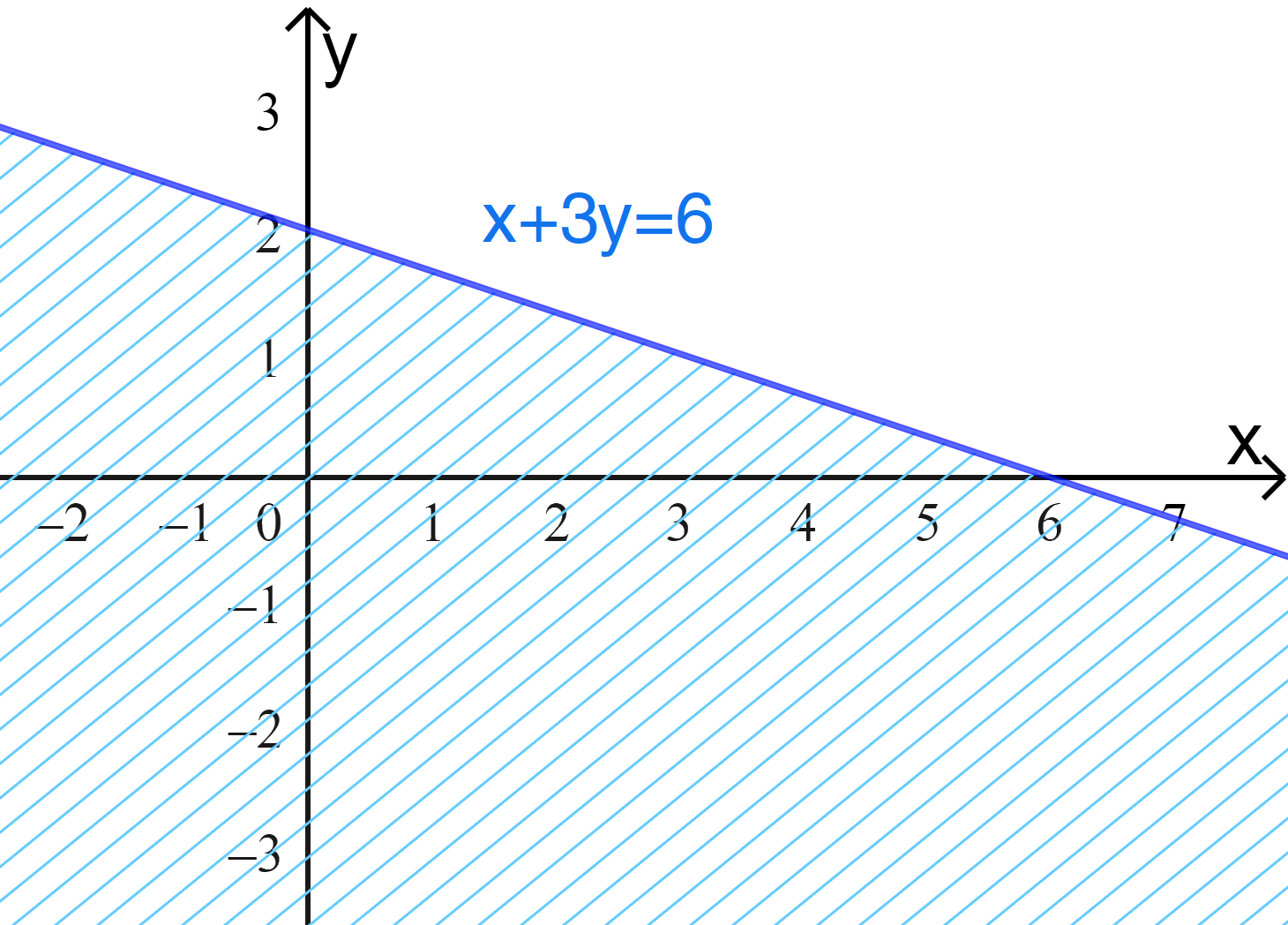
Cho bất phương trình 2x – y > 2 (3).
a) Trong mặt phẳng toạ độ Oxy, vẽ đường thẳng \(d:2x - y = 2 \Leftrightarrow y = 2x - 2\).
b) Xét điểm M(2;-1). Chứng tỏ (2;-1) là nghiệm của bất phương trình (3).
c) Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2;- 1).
Phương pháp giải:
a) Vẽ đường thẳng y = 2x - 2 trên mặt phẳng tọa độ.
b) Thay tọa độ điểm M vào bất phương trình (3), nếu thỏa mãn thì (2;-1) là một nghiệm của bất phương trình (3).
c) Gạch phần không chứa điểm M.
Lời giải chi tiết:
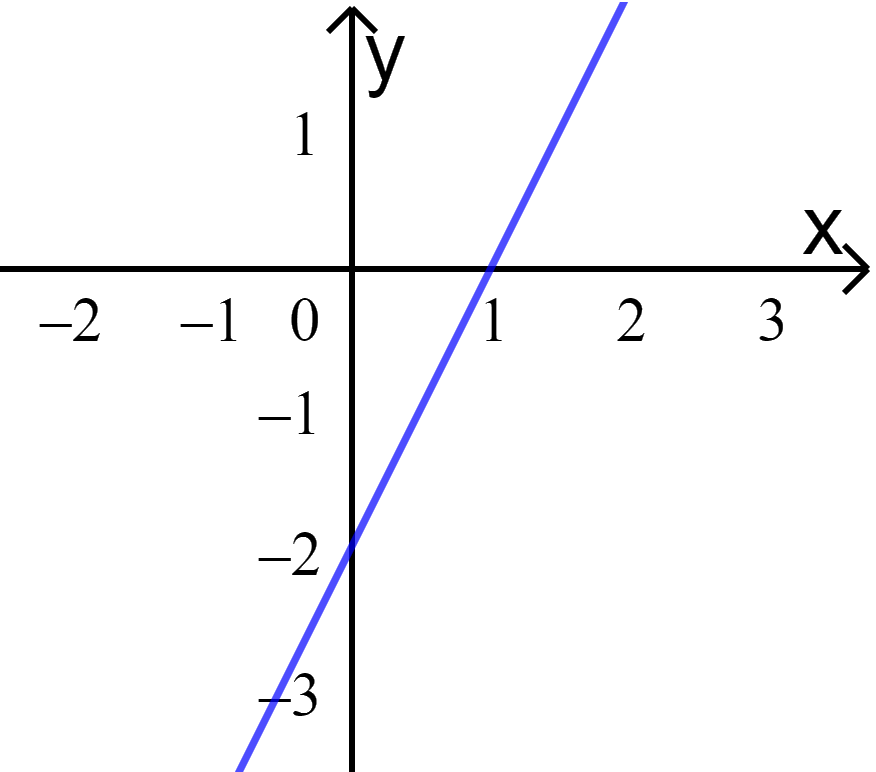
a) Cho x = 0 => y = -2.
Cho y = 0 => x = 1.
Nối hai điểm (0;-2) và (1;0) ta được:
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
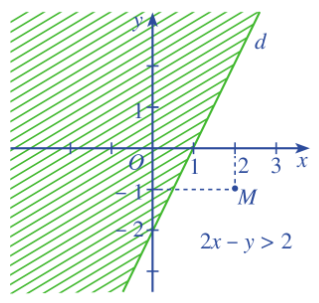
c) Ta gạch đi nửa mặt phẳng không chứa M được:
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) \(x - 2y < 4\)
b) \(x + 3y \ge 6\).
Phương pháp giải:
Các bước biểu diễn miền nghiệm:
- Vẽ đường thẳng.
- Thay tọa độ điểm O(0;0) vào bất phương trình.
- Nếu thỏa mãn thì điểm O nằm trong miền nghiệm, ta gạch phần không chứa O.
- Ngược lại thì không nằm trong miền nghiệm ta gạch phần chứa O.
Lời giải chi tiết:
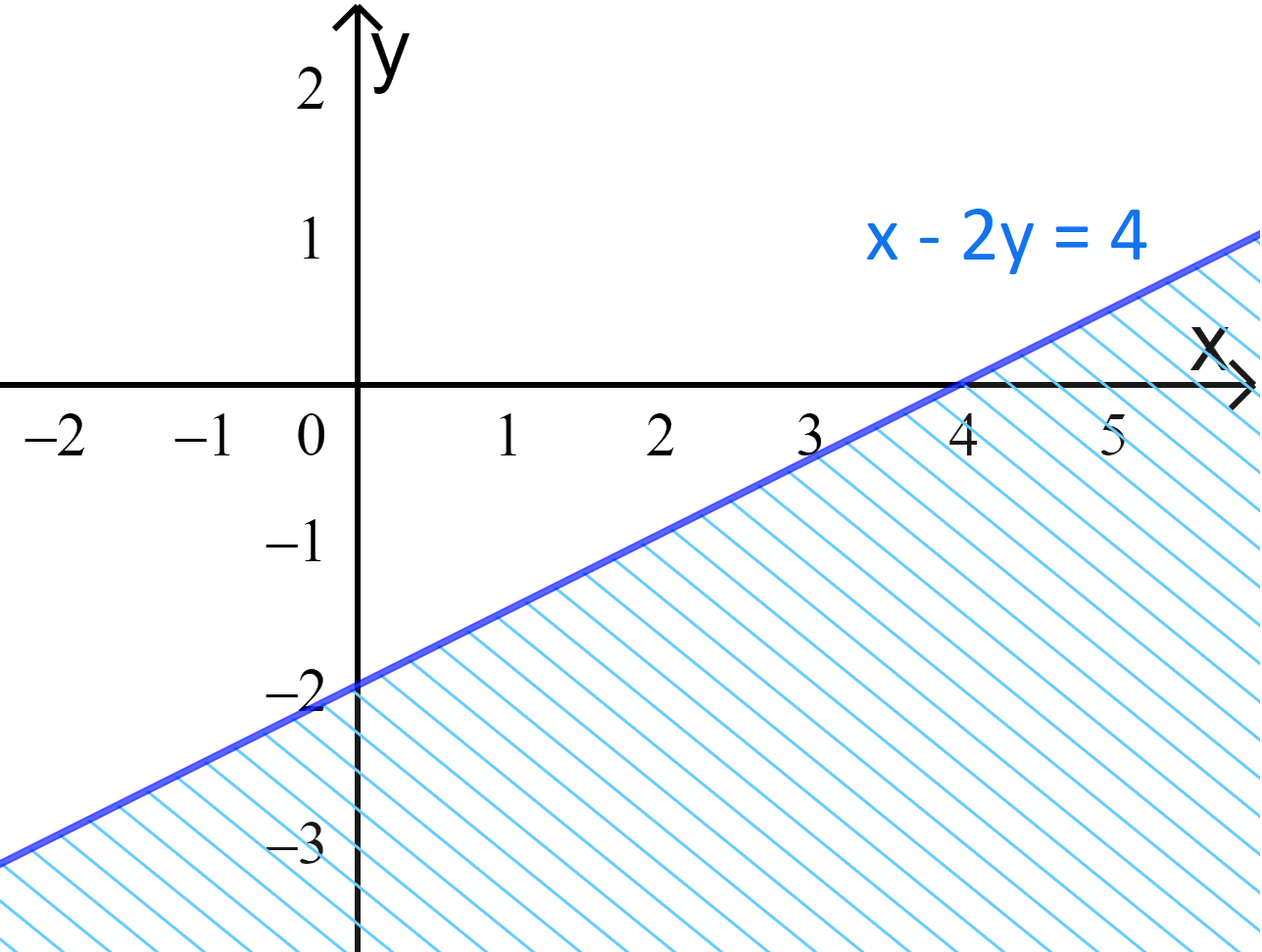
a) Ta vẽ đường thẳng d:\(x - 2y = 4 \Leftrightarrow y = \frac{x}{2} - 2\).
Cho x = 0 thì y = –2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0;–2) và (4;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x - 2y < 4\) ta được:
\(0 - 2.0 < 4\) (Luôn đúng).
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
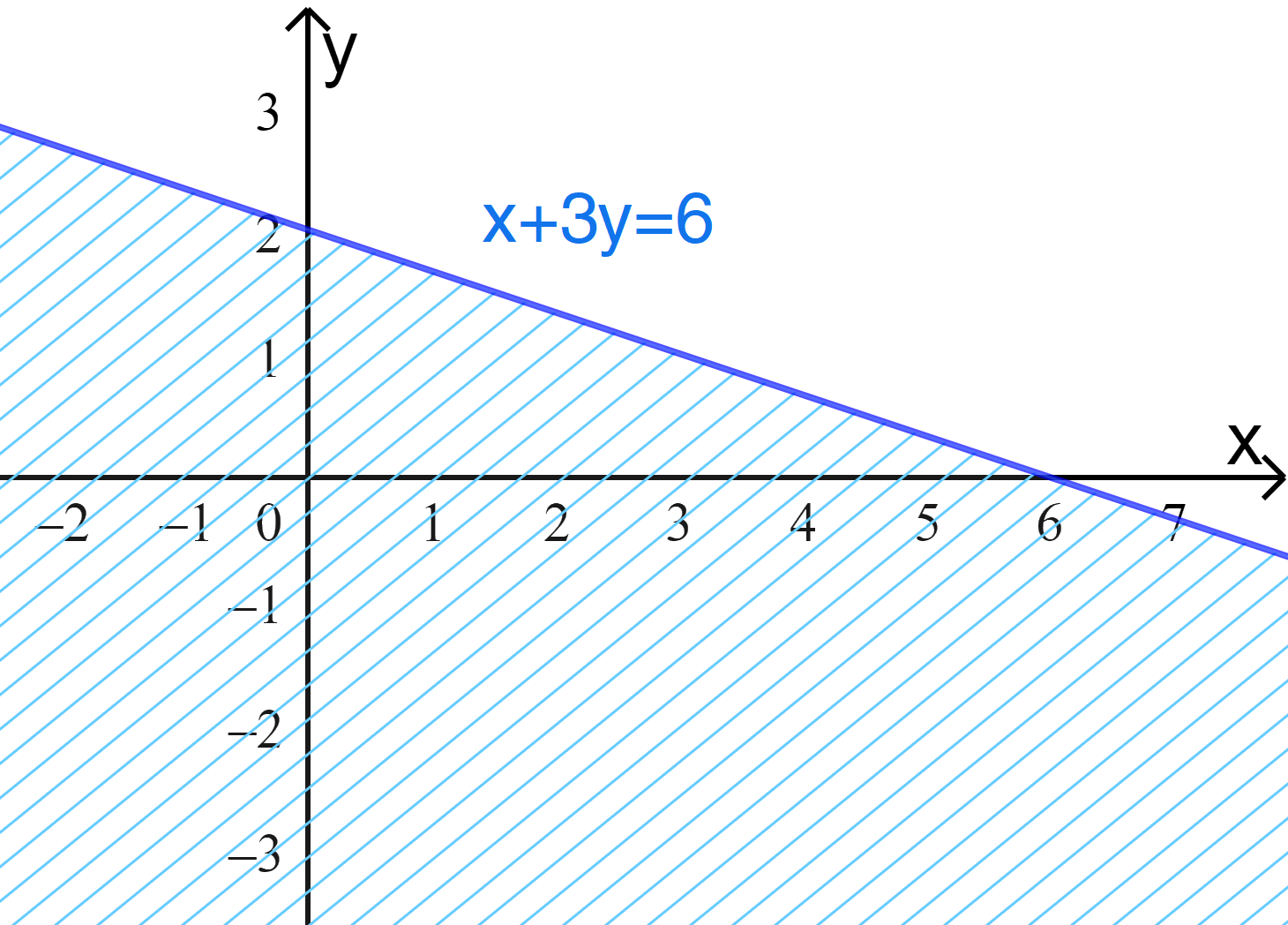
b) Ta vẽ đường thẳng d:\(x+3y=6 \).
Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0;2) và (6;0).
Thay tọa độ điểm O(0;0) vào bất phương trình \(x+3y=6 \) ta được:
\(0+3.0 < 6\).
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm:
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của tập hợp. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình Toán học.
Để giải tốt các bài tập trong Mục II, học sinh cần nắm vững các khái niệm cơ bản và các tính chất của các phép toán trên tập hợp. Dưới đây là một số phương pháp giải bài tập thường gặp:
Dưới đây là lời giải chi tiết cho các bài tập trong Mục II trang 21, 22, 23, 24 SGK Toán 10 tập 1 - Cánh diều:
Đề bài: Liệt kê các phần tử của tập hợp A = {x | x là số tự nhiên nhỏ hơn 10}.
Lời giải: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Đề bài: Cho hai tập hợp B = {1, 2, 3, 4} và C = {3, 4, 5, 6}. Tìm B ∪ C và B ∩ C.
Lời giải:
Đề bài: Cho tập hợp D = {a, b, c, d}. Tìm tập hợp các tập con của D.
Lời giải: Các tập con của D là: {}, {a}, {b}, {c}, {d}, {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}.
Đề bài: Chứng minh rằng A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
Lời giải: (Chứng minh bằng cách sử dụng định nghĩa của các phép toán trên tập hợp và các tính chất của chúng).
Để củng cố kiến thức về Mục II, các em có thể làm thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả, các em sẽ học tốt môn Toán 10 và đạt kết quả cao trong các kỳ thi.