Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục III trang 30, 31 SGK Toán 10 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
Xét mẫu số liệu được xếp theo thứ tự tăng dần: Tìm tứ phân vị của mẫu số liệu:
Xét mẫu số liệu được xếp theo thứ tự tăng dần:
1 2 3 4 5 6 7 8 9 10 11
Tìm trung vị của mẫu số liệu trên.
Lời giải chi tiết:
Mẫu số liệu trên được xếp có 11 số liệu nên \({M_e} = 6\).
Xét mẫu số liệu được xếp theo thứ tự tăng dần:
1 2 3 4 5 6 7 8 9 10 11
Tìm trung vị của mẫu số liệu trên.
Lời giải chi tiết:
Mẫu số liệu trên được xếp có 11 số liệu nên \({M_e} = 6\).
Tìm tứ phân vị của mẫu số liệu:
11 48 62 81 93 99 127
Biểu diễn tứ phân vị trên trục số.
Lời giải chi tiết:
Bước 1: Sắp xếp mẫu số liệu trên theo thứ tự không giảm
11 48 62 81 93 99 127
Bước 2: Trung vị của mẫu số liệu là: 81
Bước 3: Trung vị của dãy số 11 48 62 là: 48
Bước 4: Trung vị của dãy số 93 99 127 là: 99
Bước 5: Vậy \({Q_1} = 48,{Q_2} = 48,{Q_3} = 99\)
*) Biểu diễn tứ phân vị trên trục số:
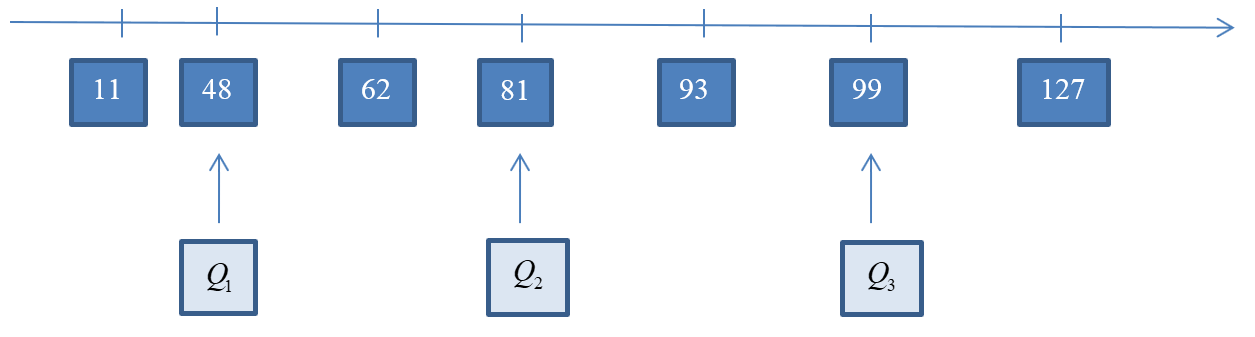
Tìm tứ phân vị của mẫu số liệu:
11 48 62 81 93 99 127
Biểu diễn tứ phân vị trên trục số.
Lời giải chi tiết:
Bước 1: Sắp xếp mẫu số liệu trên theo thứ tự không giảm
11 48 62 81 93 99 127
Bước 2: Trung vị của mẫu số liệu là: 81
Bước 3: Trung vị của dãy số 11 48 62 là: 48
Bước 4: Trung vị của dãy số 93 99 127 là: 99
Bước 5: Vậy \({Q_1} = 48,{Q_2} = 48,{Q_3} = 99\)
*) Biểu diễn tứ phân vị trên trục số:
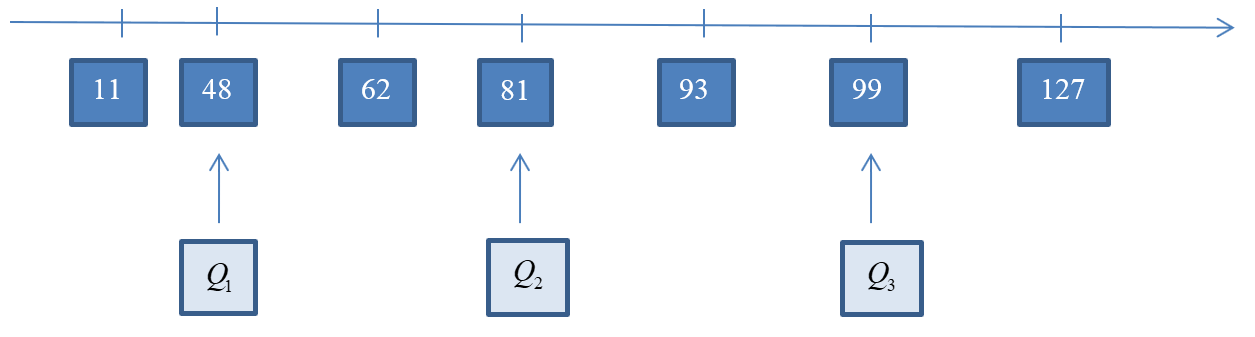
Mục III trong SGK Toán 10 tập 2 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực), và sử dụng vectơ để chứng minh các tính chất hình học.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục III trang 30, 31, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu các em xác định tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ đó. Công thức tổng quát để tính tọa độ của vectơ AB với A(xA, yA) và B(xB, yB) là:
AB = (xB - xA, yB - yA)
Các em cần nắm vững công thức này và áp dụng một cách linh hoạt để giải các bài tập tương tự.
Bài tập này yêu cầu các em thực hiện các phép toán cộng, trừ vectơ. Quy tắc cộng, trừ vectơ rất đơn giản: cộng hoặc trừ các hoành độ và tung độ tương ứng của các vectơ.
Ví dụ: Cho hai vectơ a = (x1, y1) và b = (x2, y2). Khi đó:
Bài tập này yêu cầu các em nhân một vectơ với một số thực. Quy tắc nhân vectơ với một số thực là nhân mỗi thành phần của vectơ với số thực đó.
Ví dụ: Cho vectơ a = (x, y) và số thực k. Khi đó:
ka = (kx, ky)
Đây là loại bài tập khó hơn, yêu cầu các em phải vận dụng kiến thức về vectơ để chứng minh các tính chất hình học như chứng minh hai đường thẳng song song, chứng minh hai tam giác bằng nhau, hoặc chứng minh một điểm nằm trên một đường thẳng.
Để giải loại bài tập này, các em cần:
| Công thức | Mô tả |
|---|---|
| AB = (xB - xA, yB - yA) | Tọa độ của vectơ AB |
| a + b = (x1 + x2, y1 + y2) | Phép cộng vectơ |
| a - b = (x1 - x2, y1 - y2) | Phép trừ vectơ |
| ka = (kx, ky) | Phép nhân vectơ với một số thực |
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin giải các bài tập mục III trang 30, 31 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!