Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục II trang 90 SGK Toán 10 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Lập phương trình tiếp tuyến tại điểm
Lập phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn\({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\)
Lời giải chi tiết:
Đường tròn có tâm \(I\left( {3; - 7} \right)\).
Phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn \({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\) là: \(\left( { - 1 - 3} \right)\left( {x + 1} \right) + \left( { - 4 + 7} \right)\left( {y + 4} \right) = 0 \Leftrightarrow - 4\left( {x + 1} \right) + 3\left( {y + 4} \right) = 0 \Leftrightarrow - 4x + 3y + 8 = 0\)
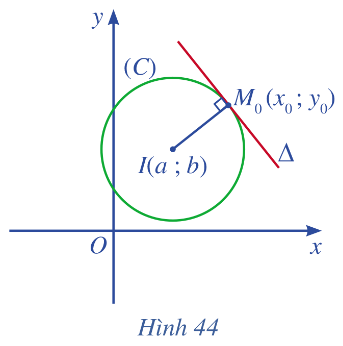
Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn (Hình 44).
a) Chứng tỏ rằng \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tính toạ độ của \(\overrightarrow {I{M_o}} \).
c) Lập phương trình tổng quát của đường thẳng \(\Delta \).
Lời giải chi tiết:
a) Do \(\Delta \) là pháp tuyến của đường tròn (C) tại điểm \({M_o}\) nên \(\Delta \) vuông góc với \(I{M_o}\). Vậy \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tọa độ \(\overrightarrow {I{M_o}} = \left( {{x_o} - a;{y_o} - b} \right)\)
c) Đường thẳng \(\Delta \)đi qua điểm \({M_o}\)và có vecto pháp tuyến \(\overrightarrow {I{M_o}} \)là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\)
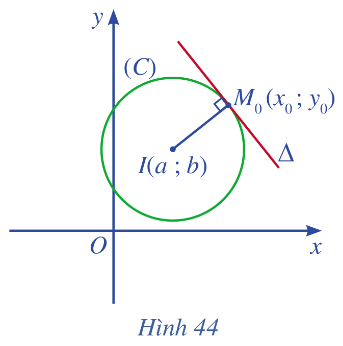
Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn (Hình 44).
a) Chứng tỏ rằng \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tính toạ độ của \(\overrightarrow {I{M_o}} \).
c) Lập phương trình tổng quát của đường thẳng \(\Delta \).
Lời giải chi tiết:
a) Do \(\Delta \) là pháp tuyến của đường tròn (C) tại điểm \({M_o}\) nên \(\Delta \) vuông góc với \(I{M_o}\). Vậy \(\overrightarrow {I{M_o}} \) là vectơ pháp tuyến của đường thẳng \(\Delta \).
b) Tọa độ \(\overrightarrow {I{M_o}} = \left( {{x_o} - a;{y_o} - b} \right)\)
c) Đường thẳng \(\Delta \)đi qua điểm \({M_o}\)và có vecto pháp tuyến \(\overrightarrow {I{M_o}} \)là: \(\left( {{x_o} - a} \right)\left( {x - {x_o}} \right) + \left( {{y_o} - b} \right)\left( {y - {y_o}} \right) = 0\)
Lập phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn\({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\)
Lời giải chi tiết:
Đường tròn có tâm \(I\left( {3; - 7} \right)\).
Phương trình tiếp tuyến tại điểm \(M\left( { - {\rm{ }}1{\rm{ }};--4} \right)\) thuộc đường tròn \({\left( {x - 3} \right)^2} + {\left( {y + 7} \right)^2} = 25\) là: \(\left( { - 1 - 3} \right)\left( {x + 1} \right) + \left( { - 4 + 7} \right)\left( {y + 4} \right) = 0 \Leftrightarrow - 4\left( {x + 1} \right) + 3\left( {y + 4} \right) = 0 \Leftrightarrow - 4x + 3y + 8 = 0\)
Mục II trang 90 SGK Toán 10 tập 2 - Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học phẳng. Các bài tập thường yêu cầu học sinh sử dụng các phép toán vectơ như cộng, trừ, nhân với một số thực, tính độ dài vectơ, tìm tọa độ vectơ, và chứng minh các đẳng thức vectơ.
Mục II bao gồm một số bài tập với mức độ khó tăng dần. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh tìm tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ đó. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ (xB - xA, yB - yA).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân với một số thực trên các vectơ đã cho. Học sinh cần nhớ các quy tắc cộng, trừ, nhân vectơ:
Bài tập này yêu cầu học sinh chứng minh một đẳng thức vectơ nào đó. Để giải bài tập này, học sinh có thể sử dụng các phương pháp sau:
Ví dụ 1: Cho A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ (3 - 1, 4 - 2) = (2, 2).
Ví dụ 2: Cho vectơ a = (1, -2) và vectơ b = (3, 1). Tính vectơ a + b.
Giải: Vectơ a + b = (1 + 3, -2 + 1) = (4, -1).
Để củng cố kiến thức và kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục II trang 90 SGK Toán 10 tập 2 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao!