Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 30 SGK Toán 10 tập 1 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng và thú vị.
Biểu diễn miền nghiệm của bất phương trình:
Đề bài
Biểu diễn miền nghiệm của bất phương trình:
a) \(3x - y > 3\)
b) \(x + 2y \le - 4\)
c) \(y \ge 2x - 5\)
Phương pháp giải - Xem chi tiết
Bước 1: Vẽ đường thẳng
Bước 2: Thay tọa độ điểm O vào bất phương trình, nếu thỏa mãn thì gạch phần không chứa O, ngược lại thì gạch phần chứa O.
Lời giải chi tiết
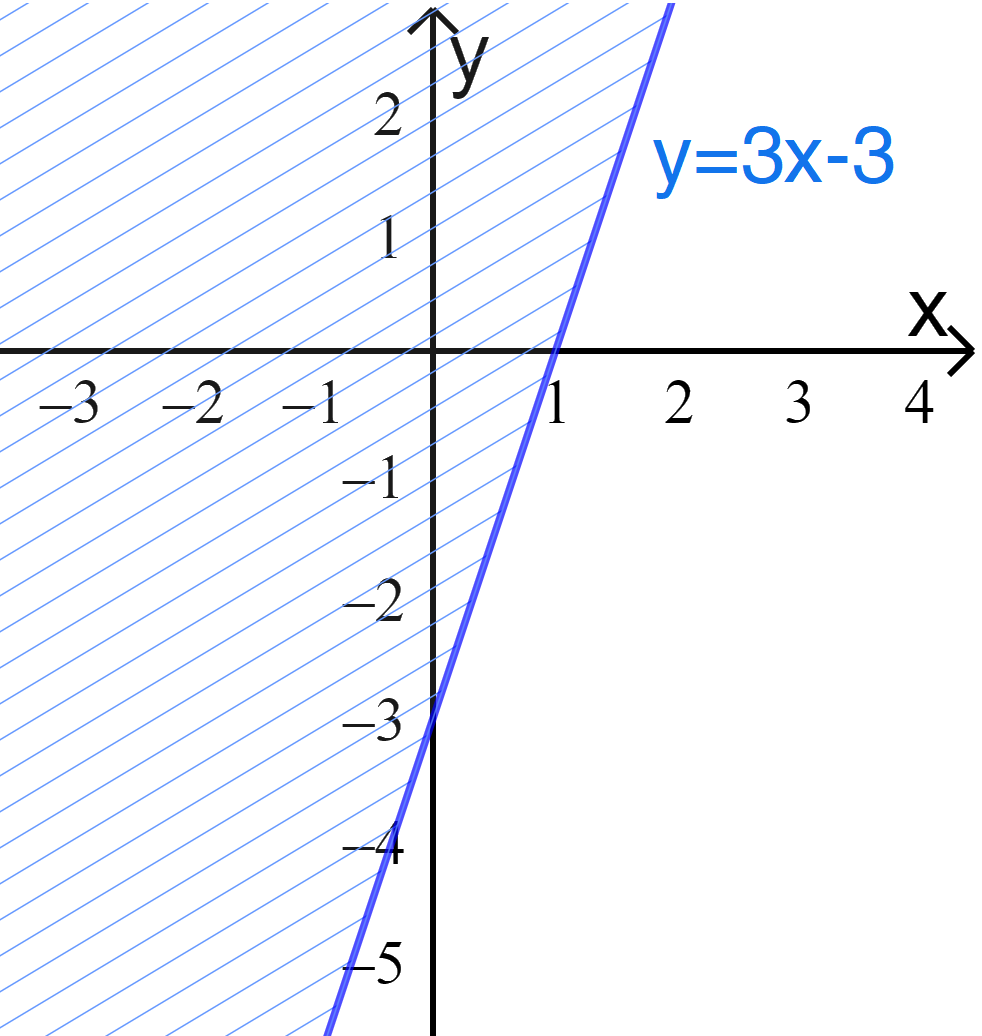
a) \(3x - y > 3\)
Bước 1: Vẽ đường thẳng \(d: 3x - y = 3 \Leftrightarrow y = 3x - 3\) đi qua A(0;-3) và B(1;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(3x - y > 3 \Leftrightarrow 3.0 - 0 > 3\)(Vô lí)
=> O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, không chứa điểm O.
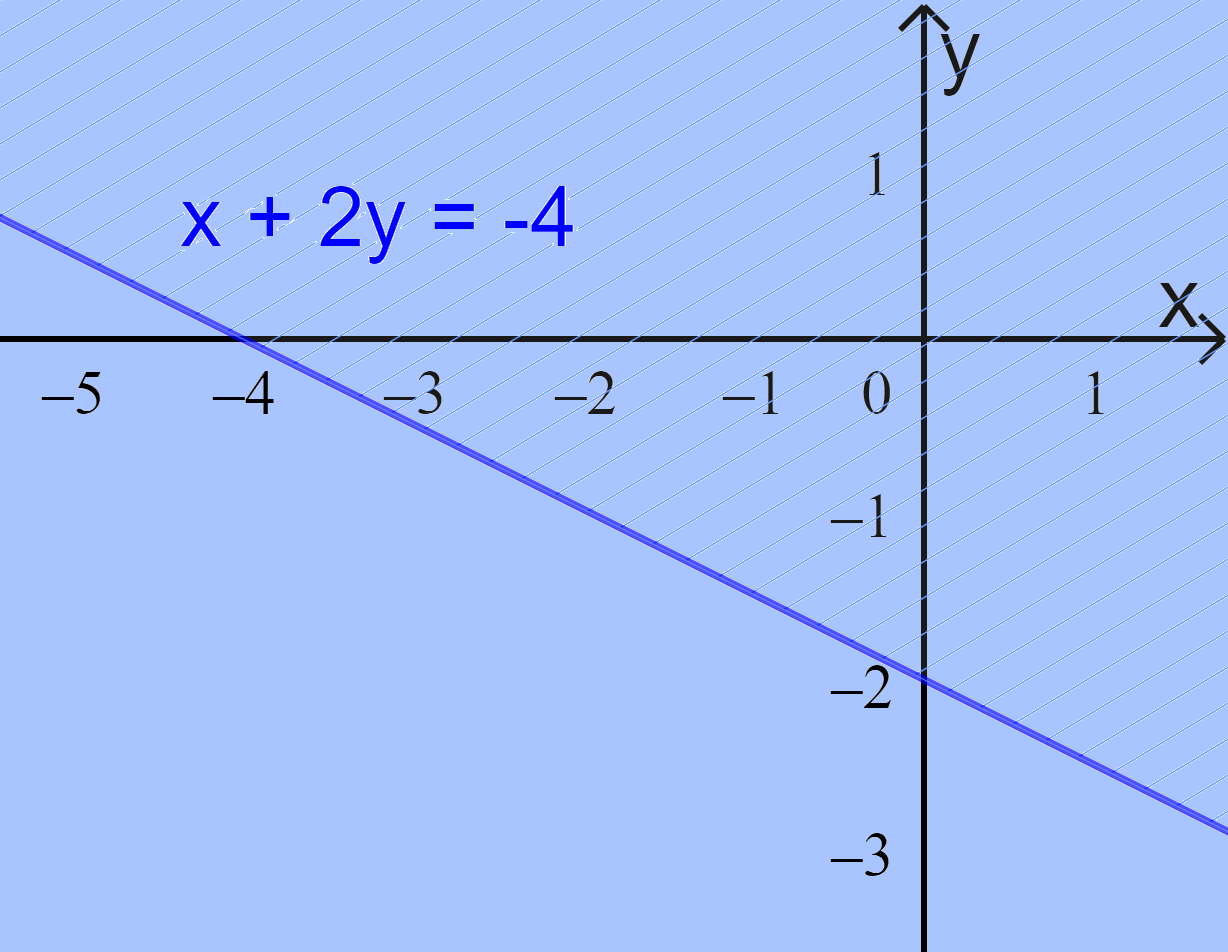
b) \(x + 2y \le - 4\)
Bước 1: Vẽ đường thẳng \(d: x + 2y = - 4 \Leftrightarrow y = - \frac{1}{2}x - 2\) đi qua A(0;-2) và B(-4;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(x + 2y \le - 4 \Leftrightarrow 0 + 2.0 \le - 4\)(Vô lí)
=> O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, không chứa điểm O.
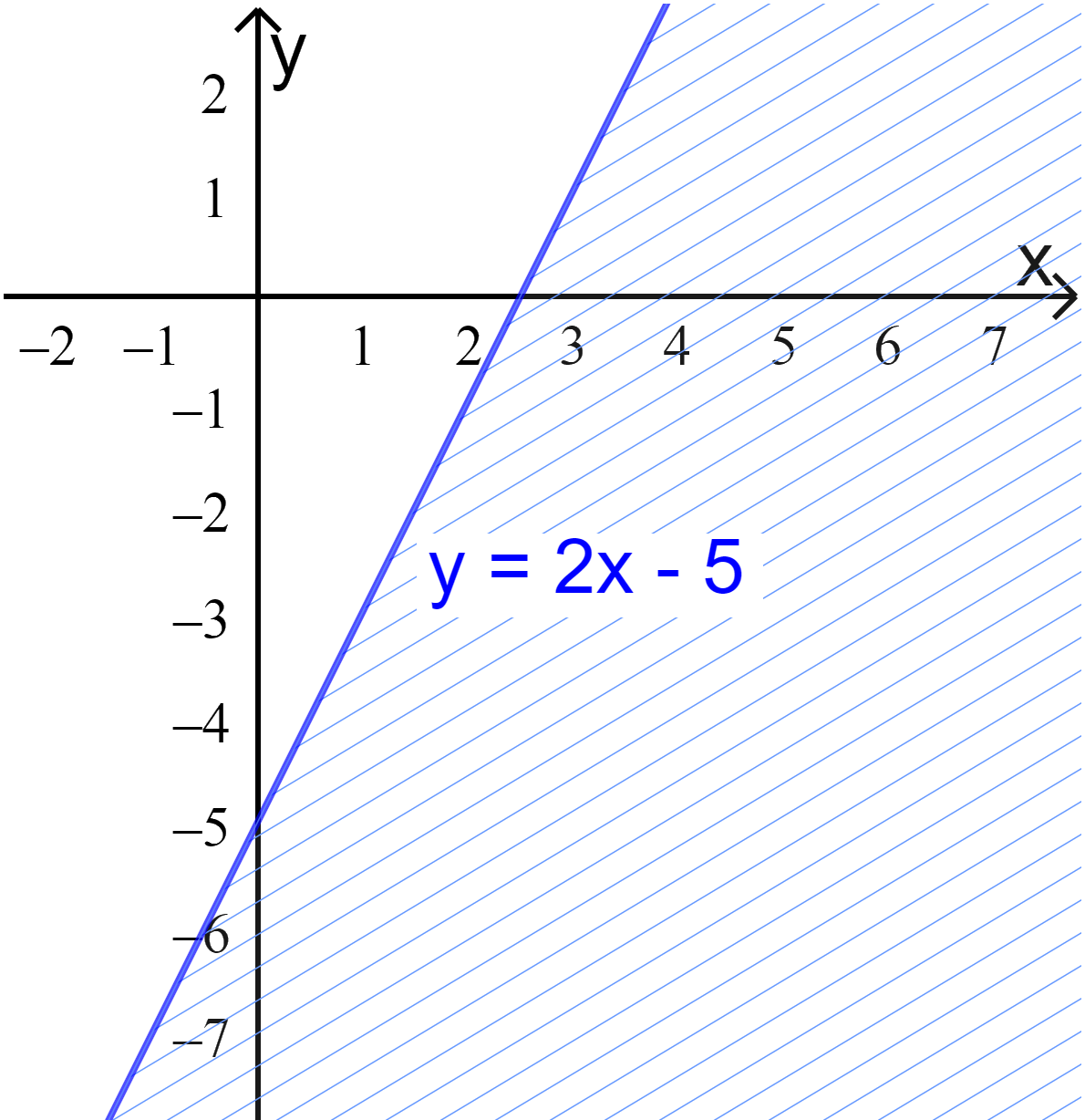
c) \(y \ge 2x - 5\)
Bước 1: Vẽ đường thẳng \(y = 2x - 5\) đi qua A(0;-5) và B(2.5;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(y \ge 2x - 5 \Leftrightarrow 0 \ge 2.0 - 5\)(Luôn đúng)
=> O thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, chứa điểm O.
Bài 1 trang 30 SGK Toán 10 tập 1 – Cánh diều thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về mệnh đề, tập hợp, các phép toán trên tập hợp để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài 1 bao gồm các câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Mệnh đề: “Nếu a là một số tự nhiên thì a là một số nguyên.”
Phân tích: Số tự nhiên là tập con của số nguyên. Do đó, nếu a là một số tự nhiên thì a chắc chắn là một số nguyên. Vậy mệnh đề này là đúng.
Mệnh đề: “Nếu a là một số nguyên thì a là một số tự nhiên.”
Phân tích: Số nguyên bao gồm số tự nhiên và số nguyên âm. Do đó, không phải mọi số nguyên đều là số tự nhiên. Ví dụ, -1 là số nguyên nhưng không phải số tự nhiên. Vậy mệnh đề này là sai.
Mệnh đề: “Nếu a là một số thực thì a là một số hữu tỉ.”
Phân tích: Số thực bao gồm số hữu tỉ và số vô tỉ. Do đó, không phải mọi số thực đều là số hữu tỉ. Ví dụ, √2 là số thực nhưng không phải số hữu tỉ. Vậy mệnh đề này là sai.
Giải:
Để giải tốt các bài tập về mệnh đề và tập hợp, các em cần:
Mệnh đề và tập hợp là những khái niệm cơ bản trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ hiểu rõ hơn về bài 1 trang 30 SGK Toán 10 tập 1 – Cánh diều và tự tin hơn trong quá trình học tập môn Toán. Chúc các em học tốt!