Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục III trang 6 và 7 sách giáo khoa Toán 10 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Sơ đồ trong Hình 4 mô tả các cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh của gia đình bạn Thảo có thể vẽ lại như sau (Hình 5):
Đề bài
Hoạt động 3 trang 6 SGK Toán 10 tập 2 – Cánh Diều
Sơ đồ trong Hình 4 mô tả các cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh của gia đình bạn Thảo có thể vẽ lại như sau (Hình 5):
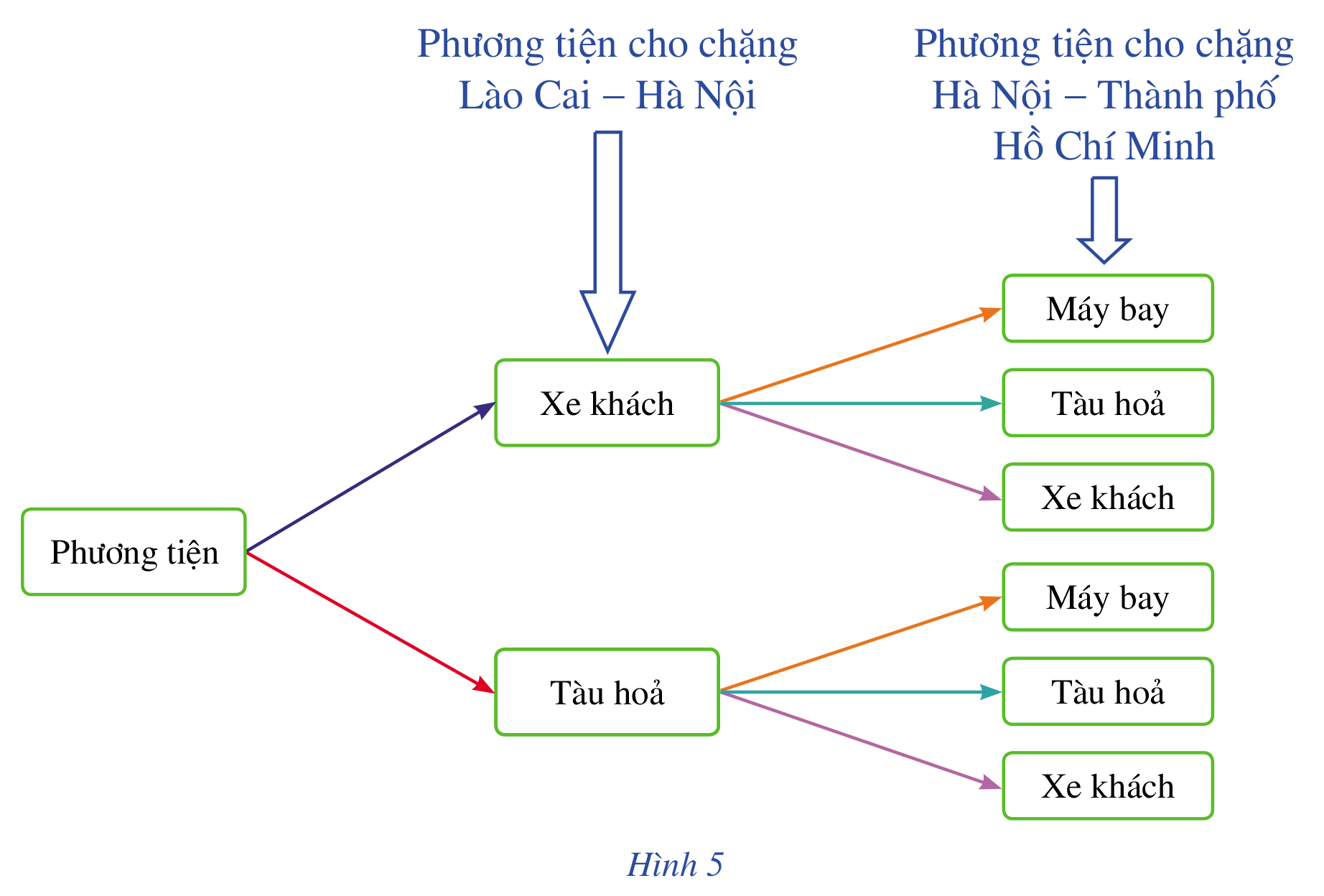
Quan sát sơ đồ Hình cây ở Hình 5, cho biết có bao nhiêu cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội.
Lời giải chi tiết
Có 6 cách chọn phương tiện đi từ Lào Cai đến Thành phố Hồ Chí Minh, qua Hà Nội.
Xe khách, Máy bay
Xe khách, Tàu hỏa
Xe khách, Xe khách
Tàu hỏa, Máy bay
Tàu hỏa, Tàu hỏa
Tàu hỏa, Xe khách
Mục III trong SGK Toán 10 tập 2 - Cánh diều tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học phẳng. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập 1 yêu cầu học sinh xác định tọa độ của các vectơ dựa trên tọa độ của các điểm trong mặt phẳng. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ khi biết tọa độ của điểm đầu và điểm cuối: Nếu A(xA, yA) và B(xB, yB) thì AB = (xB - xA, yB - yA).
Bài tập 2 tập trung vào việc thực hiện các phép toán cộng, trừ vectơ và nhân vectơ với một số thực. Để giải bài tập này, học sinh cần nhớ các quy tắc sau:
Bài tập 3 yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, hoặc chứng minh một tứ giác là hình bình hành. Để giải bài tập này, học sinh cần kết hợp kiến thức về vectơ với các định lý và tính chất hình học đã học.
Đề bài: Cho A(1, 2) và B(3, 4). Tìm tọa độ của vectơ AB.
Lời giải:
Áp dụng công thức tính tọa độ của vectơ, ta có:
AB = (3 - 1, 4 - 2) = (2, 2)
Vậy, tọa độ của vectơ AB là (2, 2).
Đề bài: Cho vectơ a = (1, -2) và vectơ b = (3, 1). Tính vectơ a + b và vectơ 2a.
Lời giải:
a + b = (1 + 3, -2 + 1) = (4, -1)
2a = 2(1, -2) = (2, -4)
Vậy, vectơ a + b là (4, -1) và vectơ 2a là (2, -4).
Đề bài: Cho A(1, 1), B(2, 3) và C(3, 1). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải:
Để chứng minh ba điểm A, B, C thẳng hàng, ta cần chứng minh rằng vectơ AB và vectơ AC cùng phương. Tính vectơ AB và vectơ AC:
AB = (2 - 1, 3 - 1) = (1, 2)
AC = (3 - 1, 1 - 1) = (2, 0)
Kiểm tra xem hai vectơ AB và AC có cùng phương hay không bằng cách xét tỉ số giữa các tọa độ tương ứng:
1/2 ≠ 2/0
Vì tỉ số giữa các tọa độ tương ứng không bằng nhau, nên hai vectơ AB và AC không cùng phương. Do đó, ba điểm A, B, C không thẳng hàng.
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em học sinh đã có thể tự tin giải các bài tập trong mục III trang 6, 7 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!