Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục I trang 44, 45 SGK Toán 10 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 10.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích từng dạng bài tập, cùng với những lưu ý quan trọng để các em đạt kết quả tốt nhất.
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai f(x) = x^2 - 2x + 2 b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai f(x) = - x^2 + 4x - 4
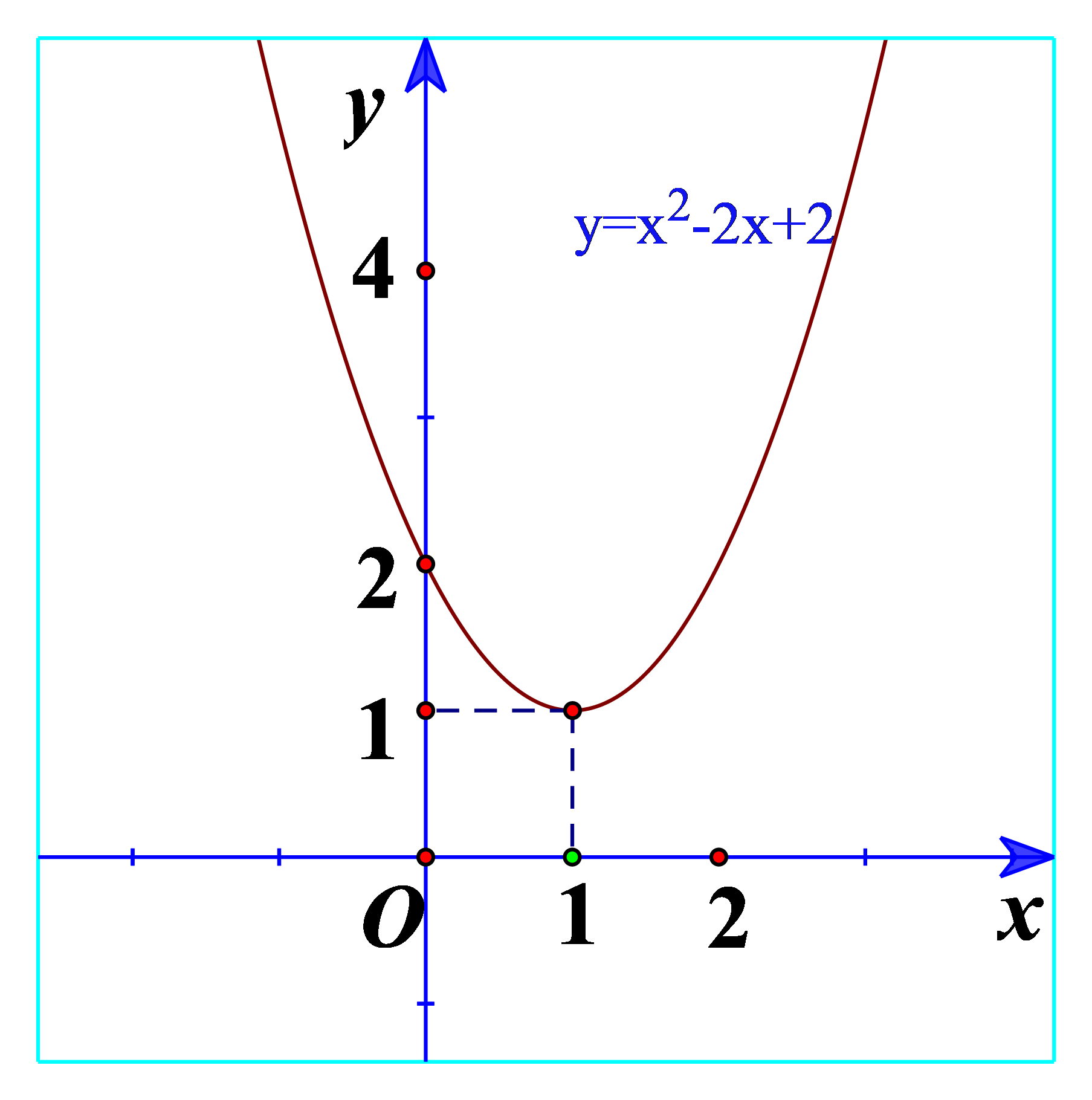
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - 2x + 2\)
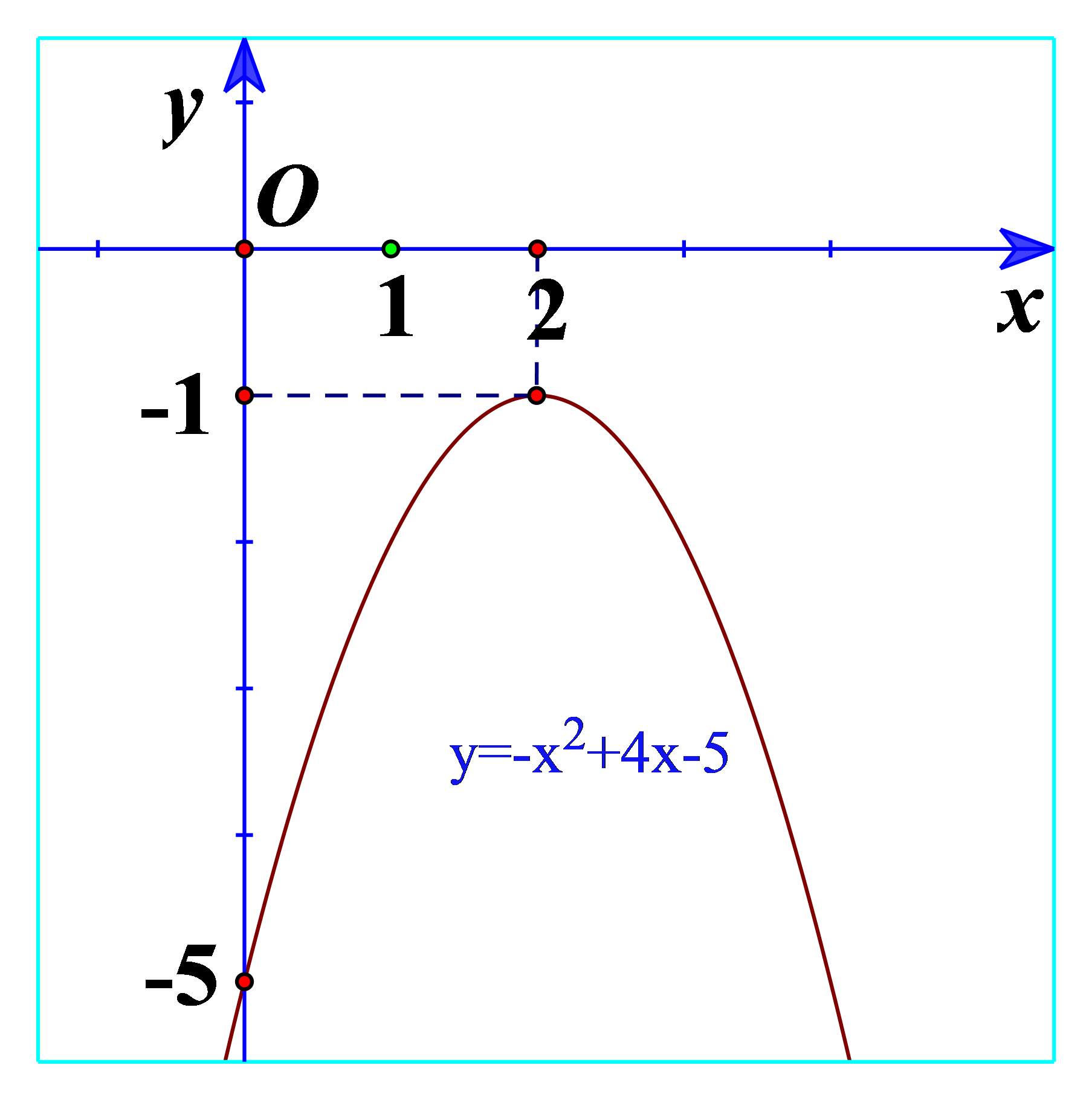
b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 5\)
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta < 0\).
Phương pháp giải:
a) \(a{x^2} + bx + c > 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía trên trục hoành.
b) \(a{x^2} + bx + c < 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía dưới trục hoành.
c) Rút ra nhận xét.
Lời giải chi tiết:
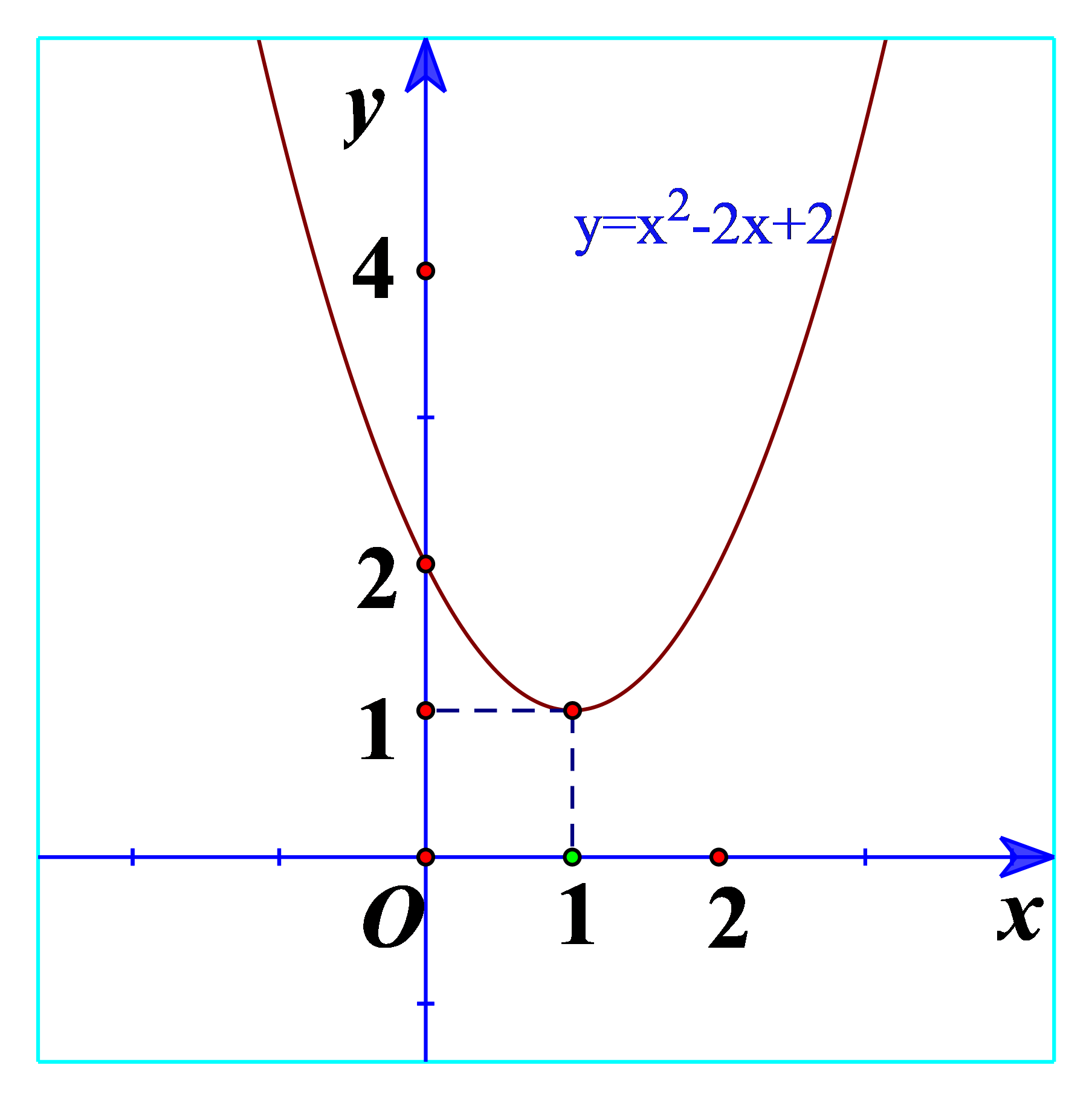
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
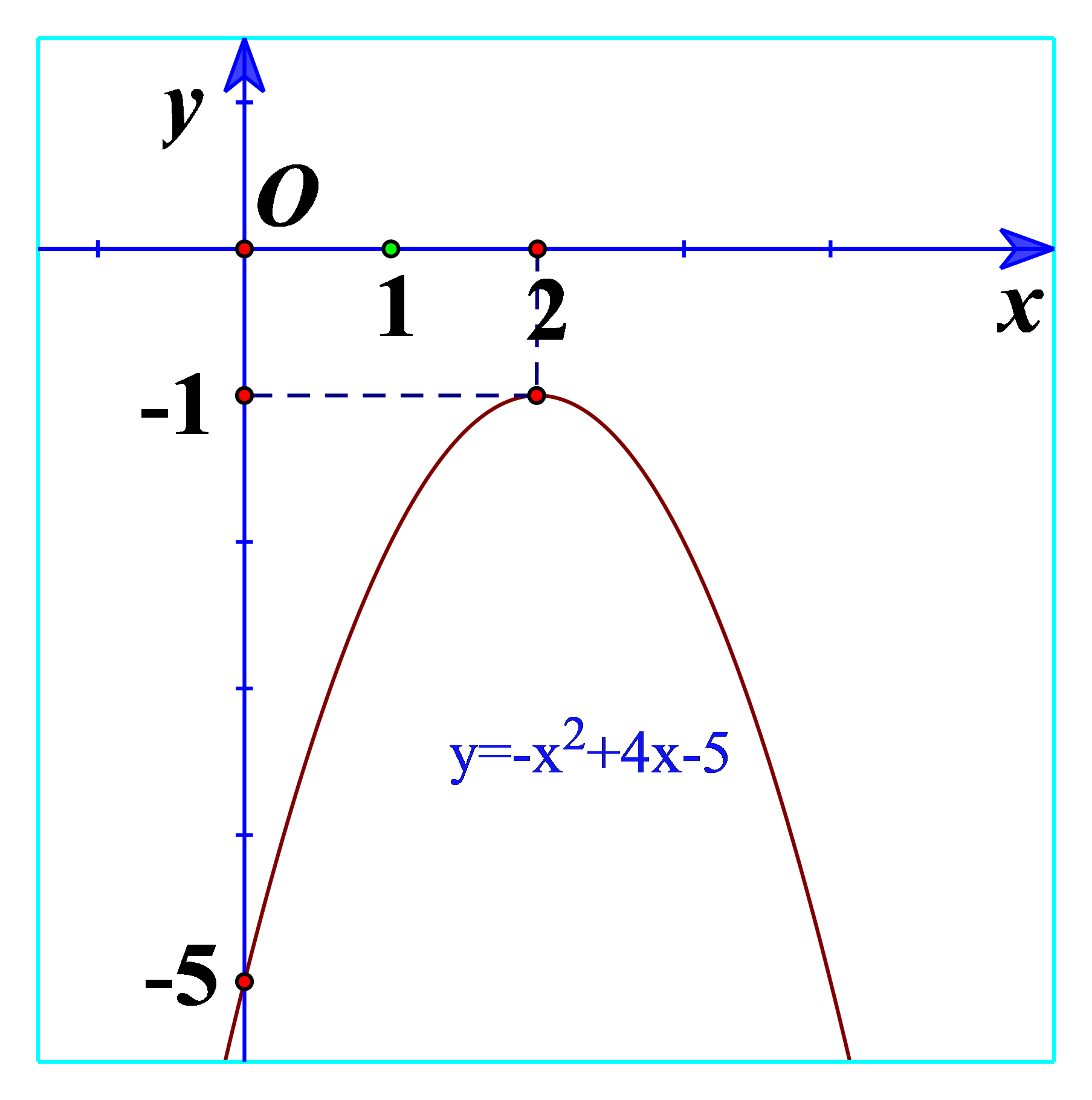
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
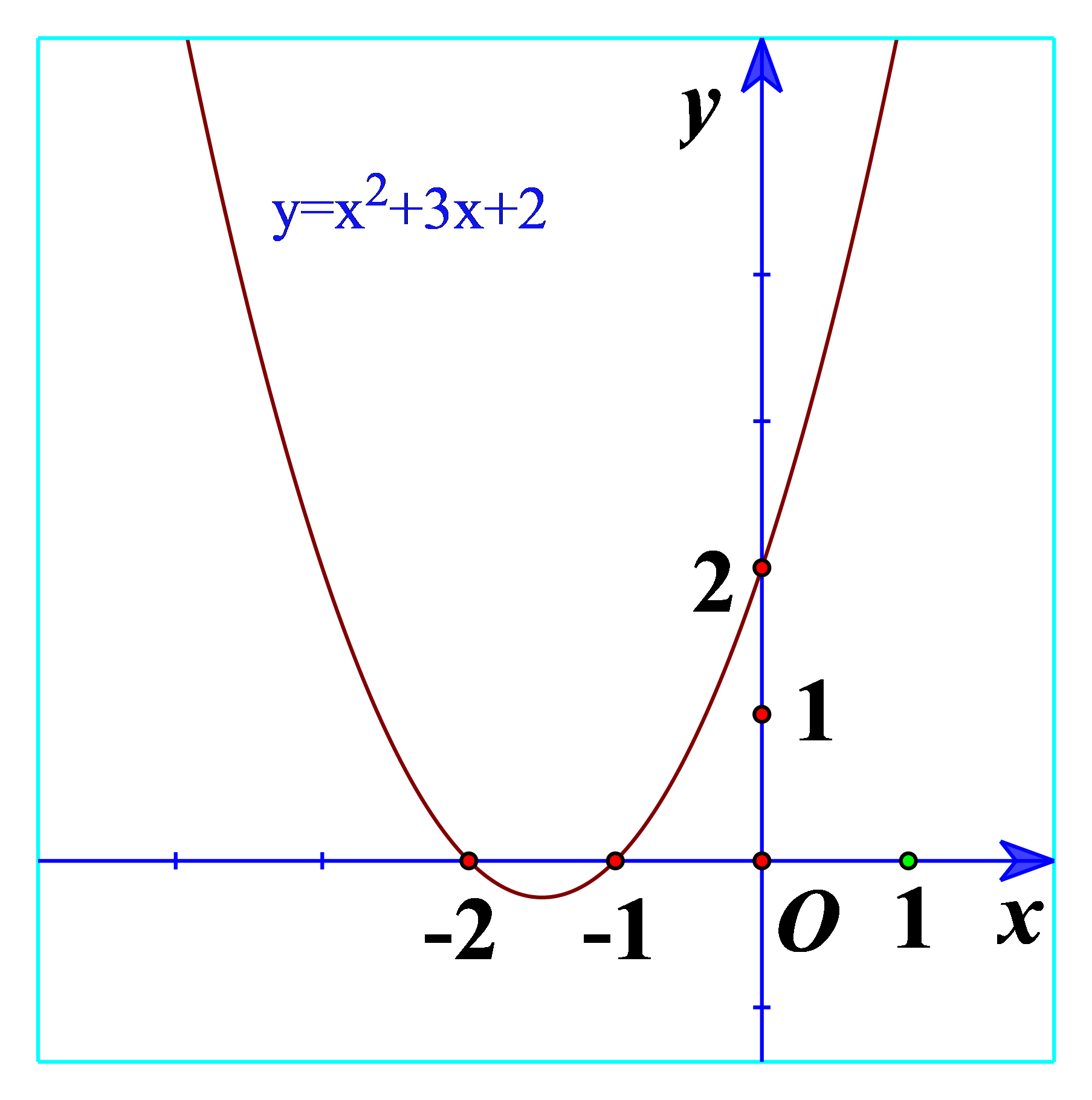
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.
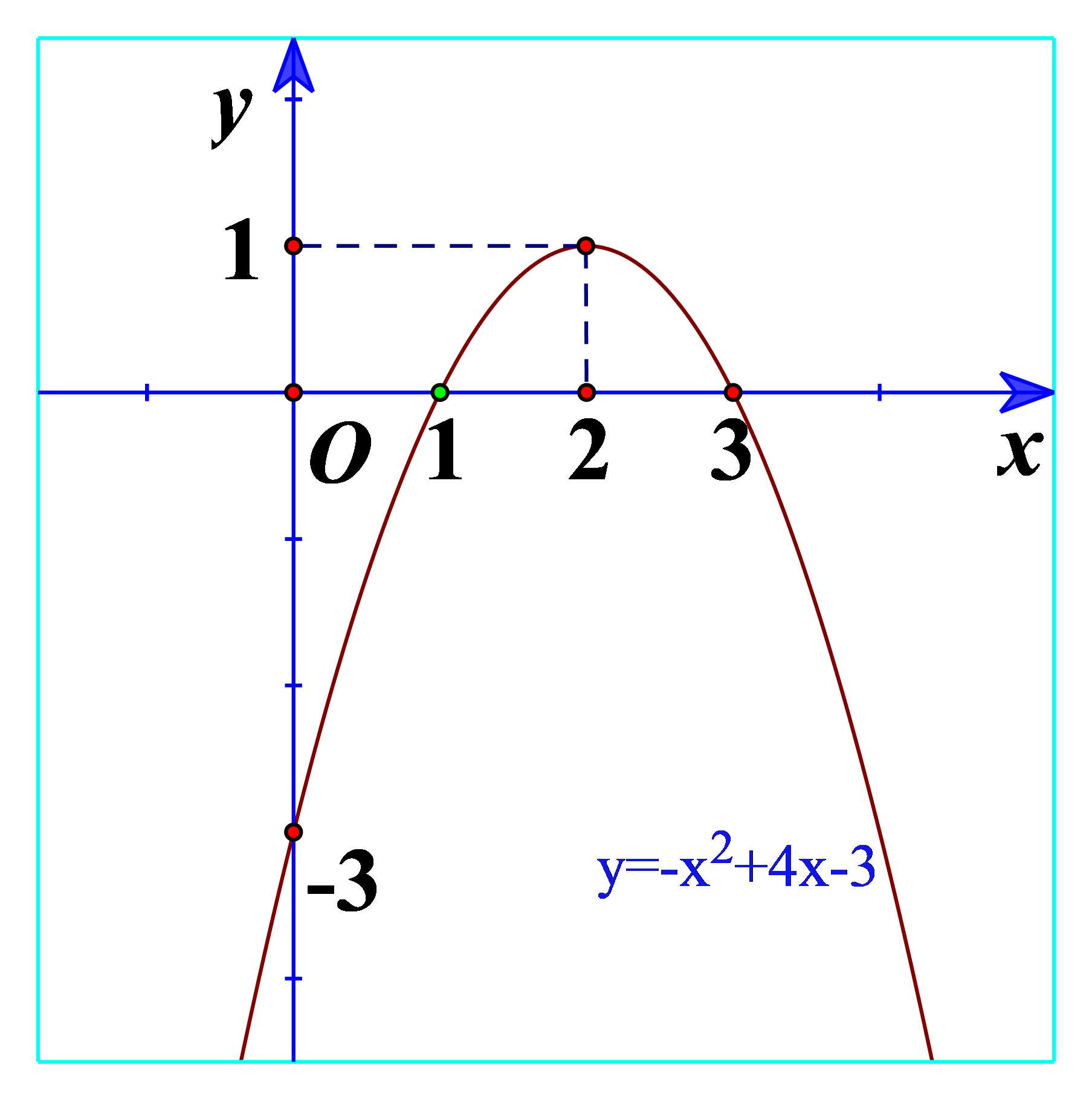
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x.
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\).
Phương pháp giải:
a) Xét các khoảng \(\left( { - \infty ; - 2} \right);\left( { - 2; - 1} \right);\left( { - 1; + \infty } \right)\)
b) Xét các khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\)
c) Rút ra nhận xét.
Lời giải chi tiết:
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
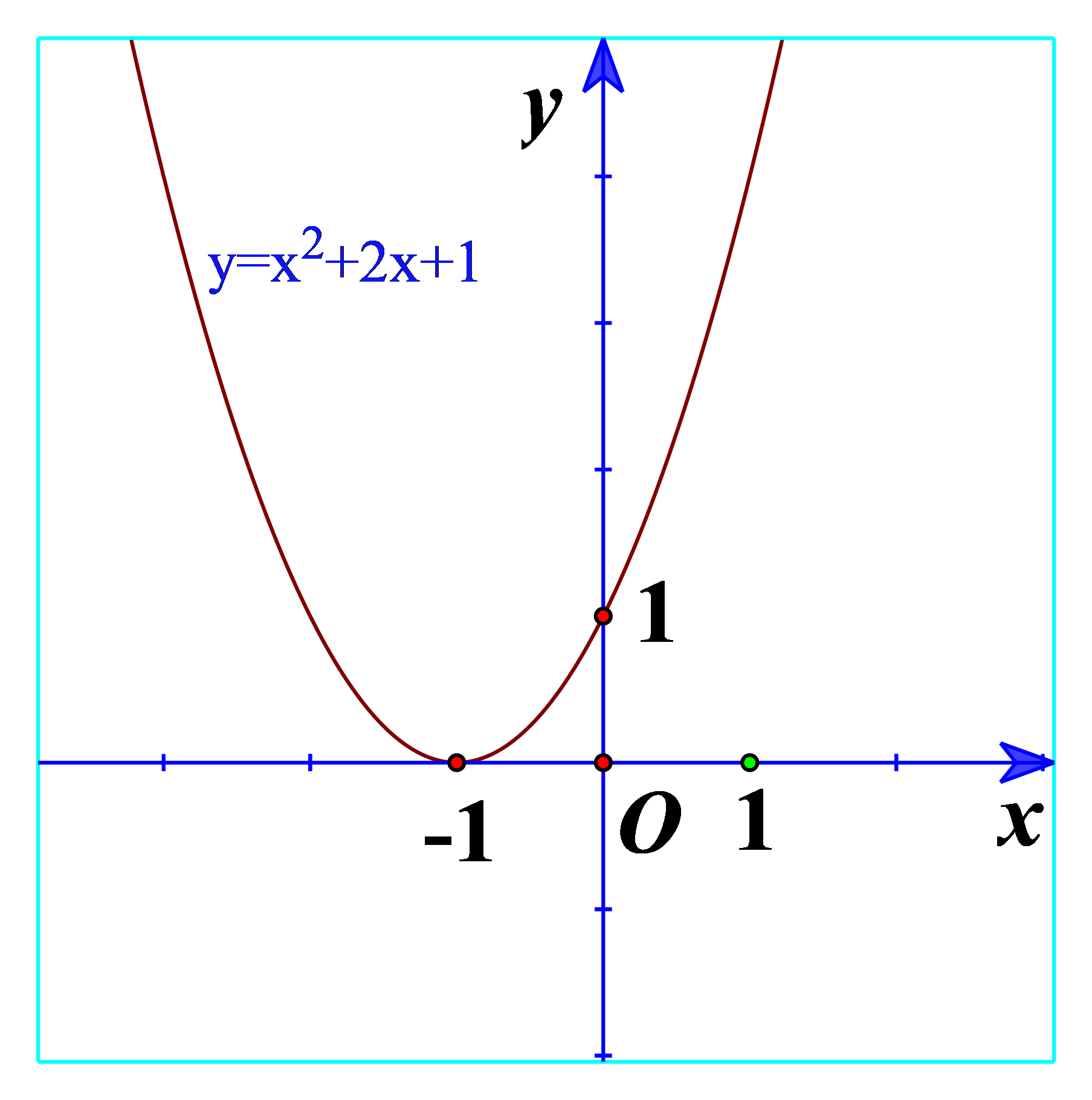
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\)
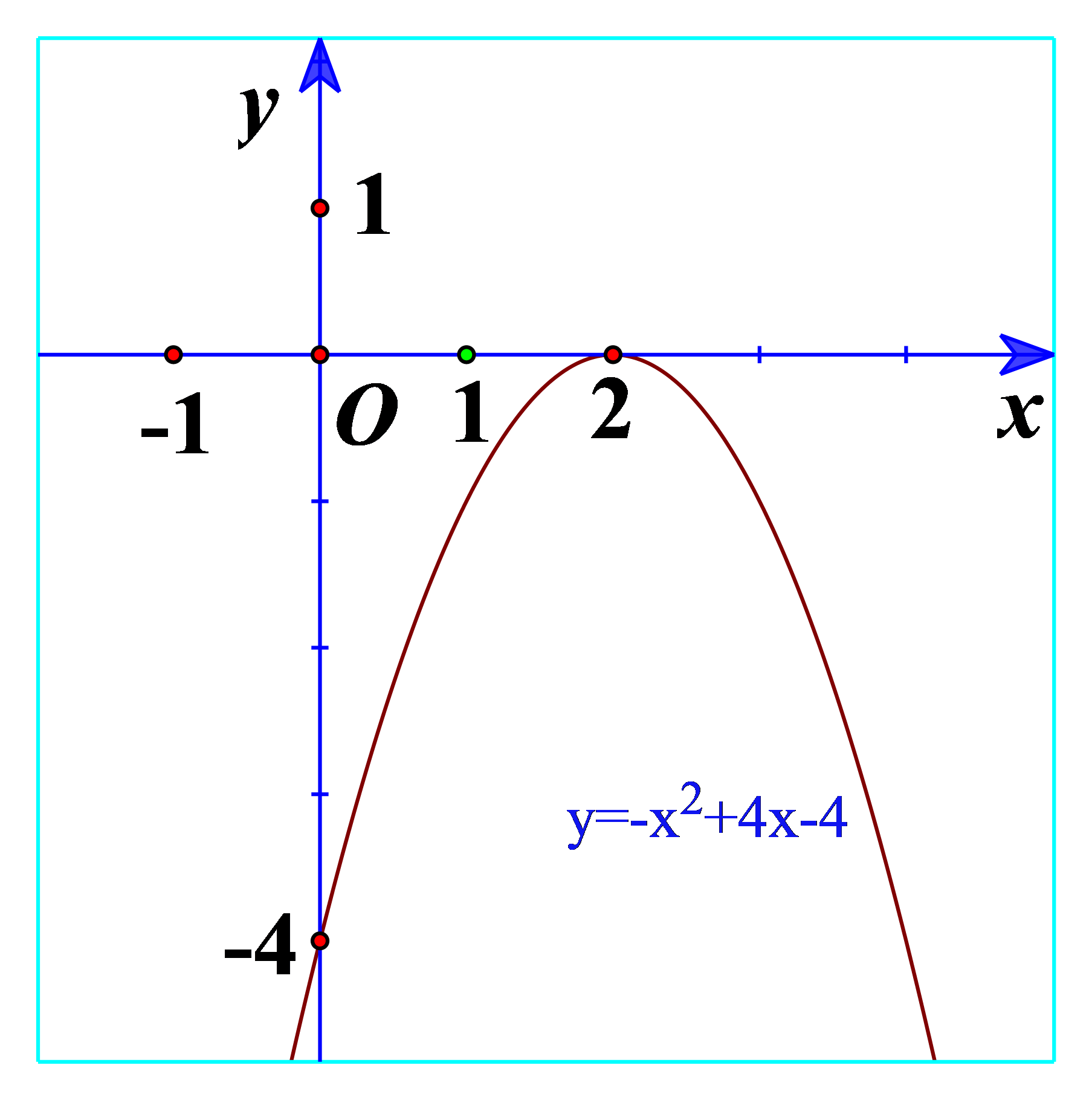
b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\)
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta = 0\).
Phương pháp giải:
a) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\).
b) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\).
c) Rút ra nhận xét.
Lời giải chi tiết:
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - 2x + 2\)
b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 5\)
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta < 0\).
Phương pháp giải:
a) \(a{x^2} + bx + c > 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía trên trục hoành.
b) \(a{x^2} + bx + c < 0\) ứng với phần parabol \(y = a{x^2} + bx + c\) nằm phía dưới trục hoành.
c) Rút ra nhận xét.
Lời giải chi tiết:
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
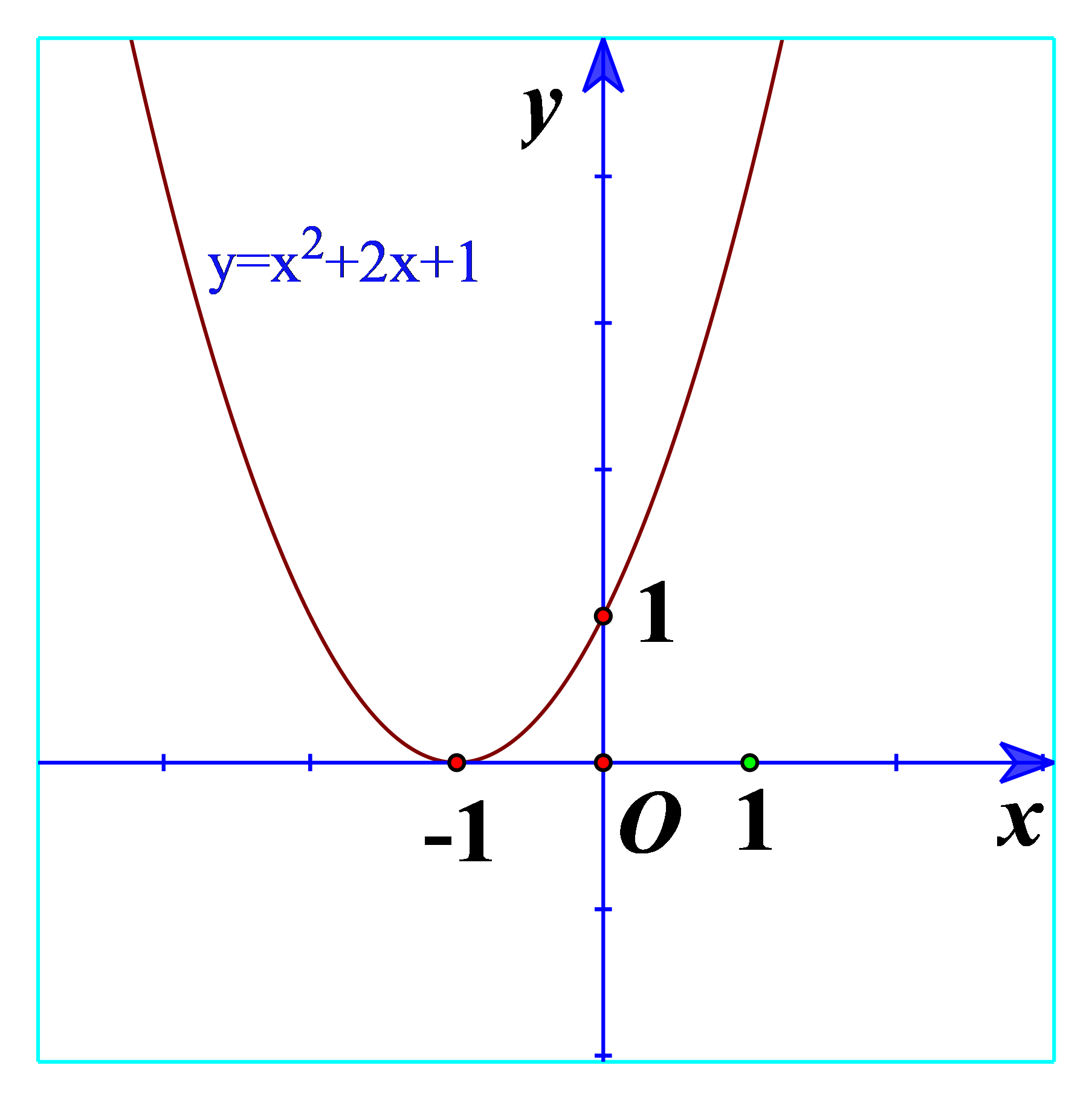
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\)
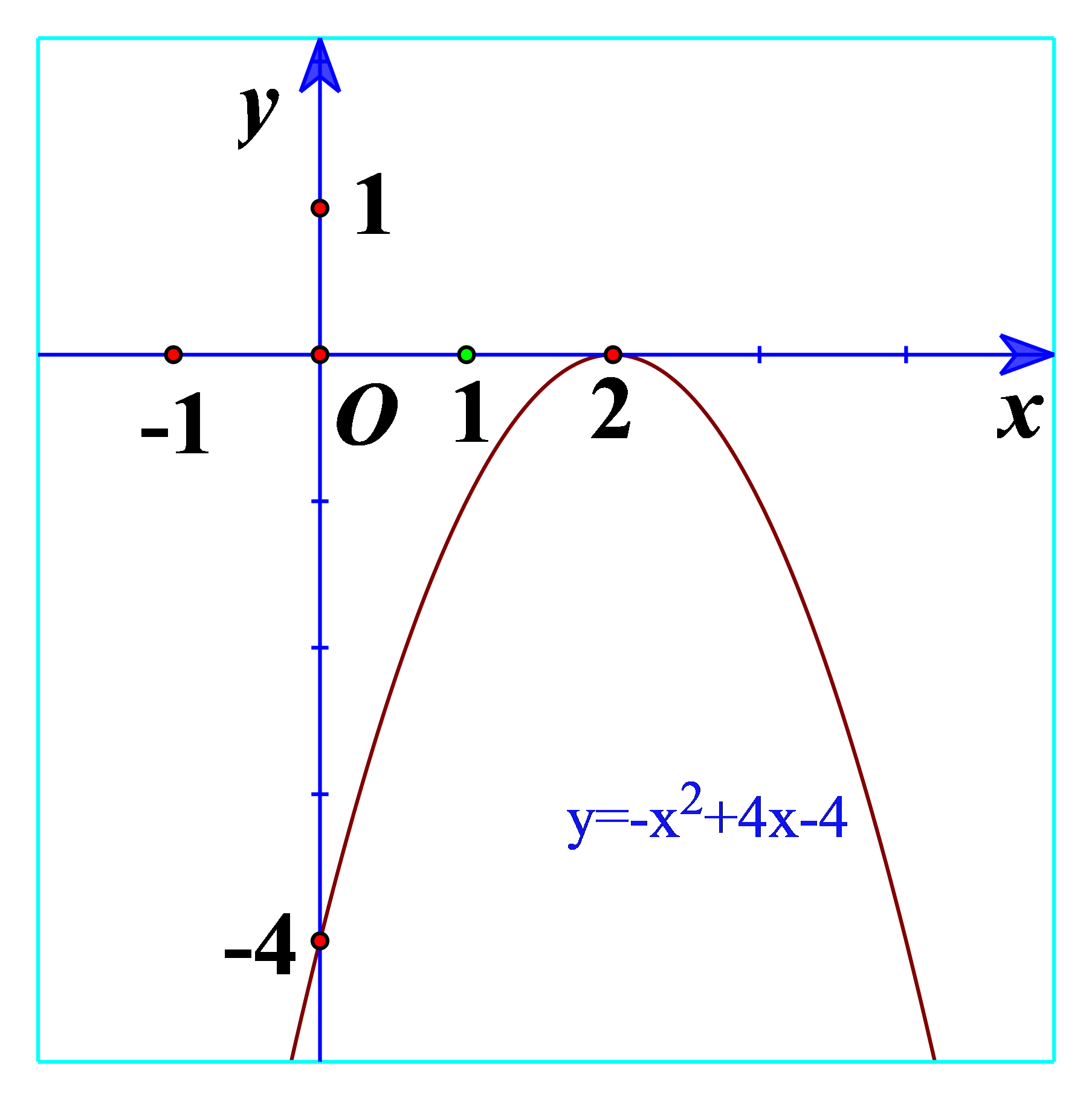
b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\)
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta = 0\).
Phương pháp giải:
a) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\).
b) Xét giao điểm của đồ thị và trục hoành. Xét dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\).
c) Rút ra nhận xét.
Lời giải chi tiết:
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
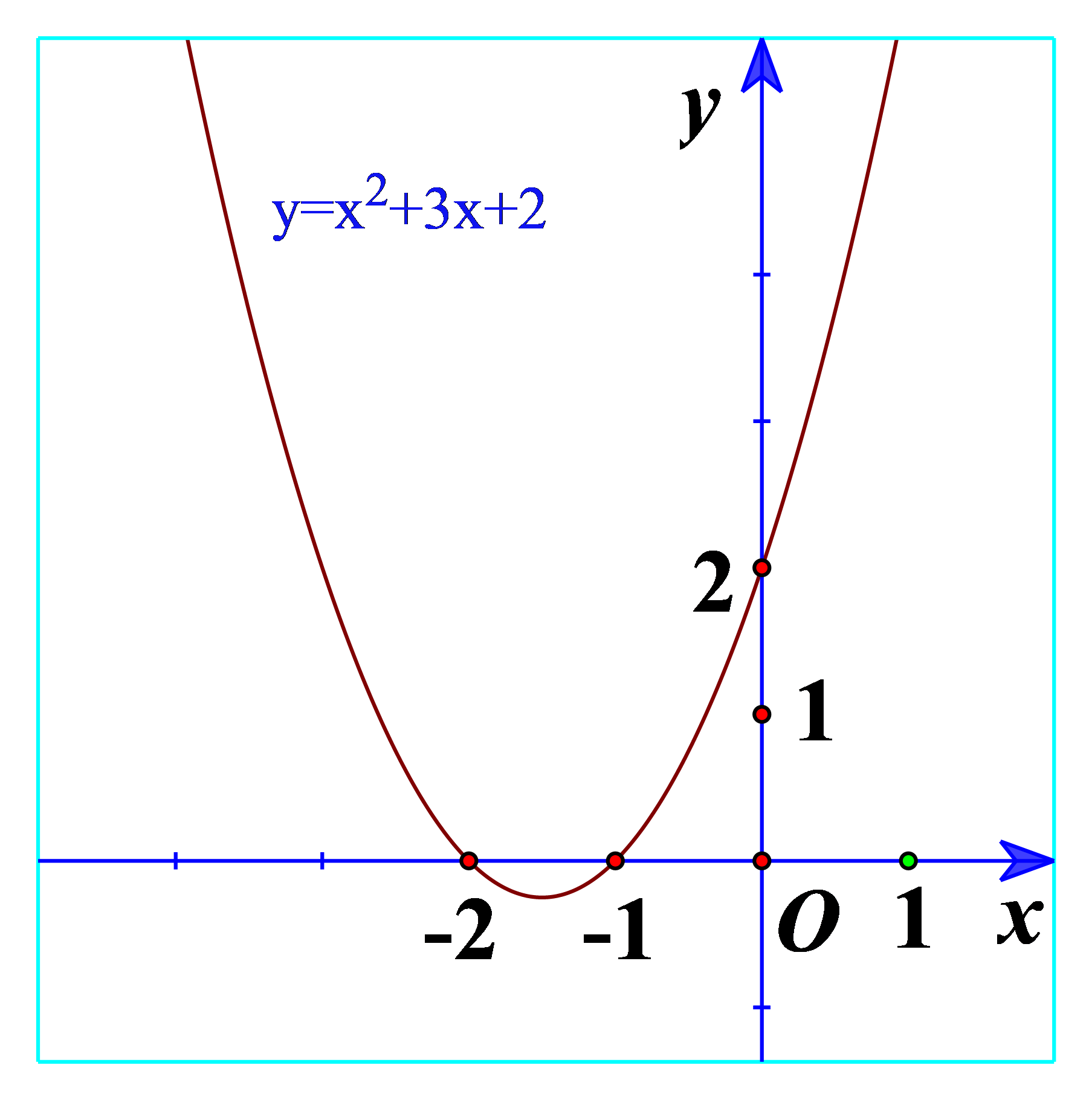
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.
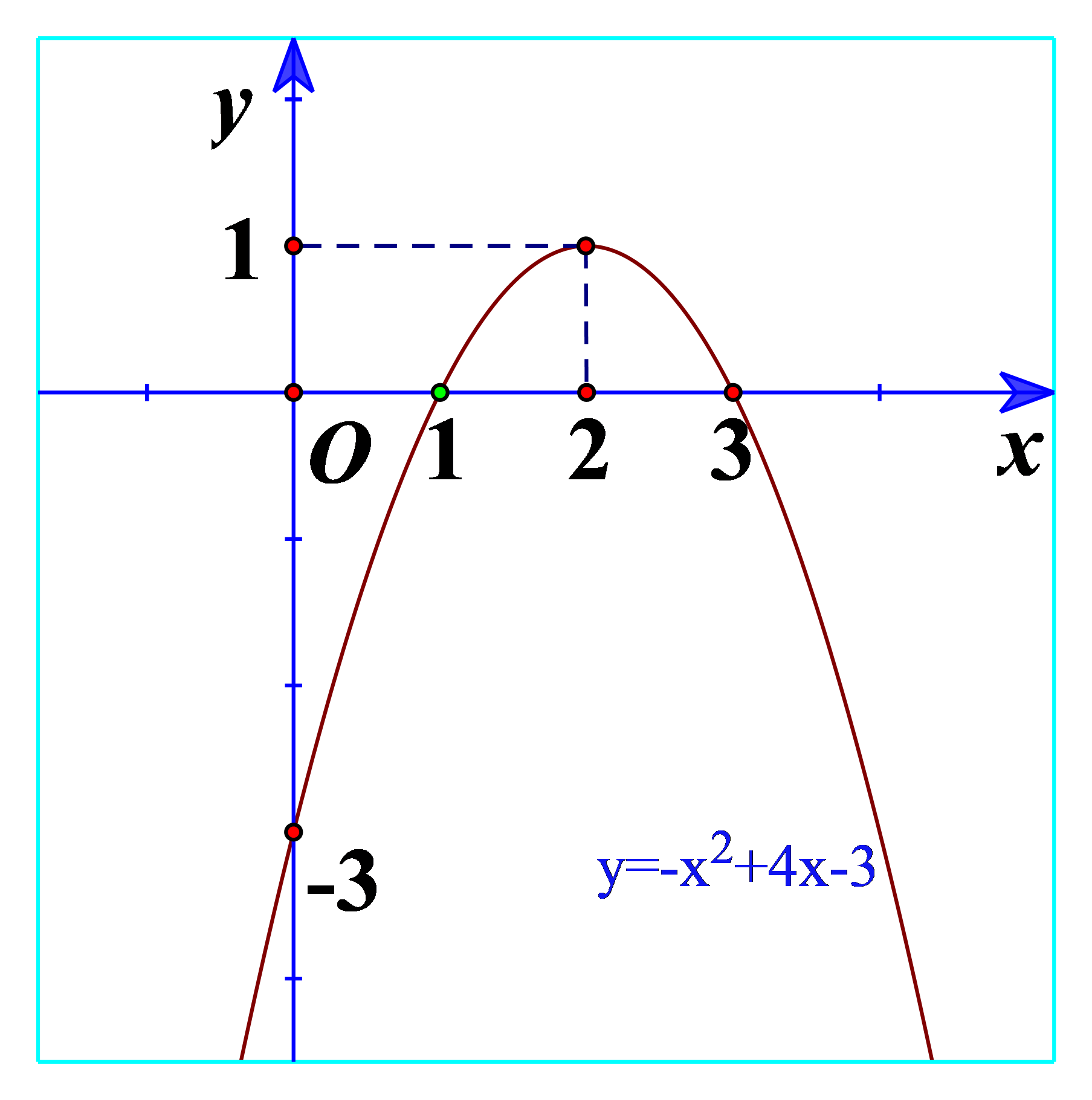
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x.
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\).
Phương pháp giải:
a) Xét các khoảng \(\left( { - \infty ; - 2} \right);\left( { - 2; - 1} \right);\left( { - 1; + \infty } \right)\)
b) Xét các khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\)
c) Rút ra nhận xét.
Lời giải chi tiết:
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
Mục I trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 10.
Bài tập mục I trang 44, 45 SGK Toán 10 tập 1 - Cánh diều bao gồm nhiều dạng bài tập khác nhau, từ việc xác định các phần tử của tập hợp, tìm giao, hợp, hiệu của các tập hợp, đến việc chứng minh các đẳng thức tập hợp. Dưới đây là giải chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định các tập hợp dựa trên các điều kiện cho trước. Ví dụ, cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy xác định tập hợp A ∪ B (hợp của A và B).
Lời giải: A ∪ B = {1, 2, 3, 4, 5, 6, 7}
Bài tập này yêu cầu học sinh tìm giao của các tập hợp. Ví dụ, cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy xác định tập hợp A ∩ B (giao của A và B).
Lời giải: A ∩ B = {3, 4, 5}
Bài tập này yêu cầu học sinh tìm hiệu của các tập hợp. Ví dụ, cho tập hợp A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy xác định tập hợp A \ B (hiệu của A và B).
Lời giải: A \ B = {1, 2}
Bài tập này yêu cầu học sinh chứng minh các đẳng thức tập hợp. Ví dụ, chứng minh rằng A ∪ B = B ∪ A.
Lời giải: Để chứng minh A ∪ B = B ∪ A, ta cần chứng minh rằng mọi phần tử thuộc A ∪ B thì cũng thuộc B ∪ A, và ngược lại.
Tương tự, ta có thể chứng minh rằng mọi phần tử thuộc B ∪ A thì cũng thuộc A ∪ B.
Ngoài các dạng bài tập cơ bản như trên, còn có một số dạng bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải bài tập về tập hợp một cách hiệu quả, học sinh cần lưu ý những điều sau:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập mục I trang 44, 45 SGK Toán 10 tập 1 - Cánh diều. Chúc các em học tốt!