Chào mừng bạn đến với bài học về Lý thuyết Hàm số bậc hai, một chủ đề quan trọng trong chương trình Toán 10 Cánh diều. Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về hàm số bậc hai, cách vẽ đồ thị và các ứng dụng thực tế của nó.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và bài tập đa dạng để bạn có thể nắm vững kiến thức một cách nhanh chóng và hiệu quả.
I. Hàm số bậc hai II. Đồ thị hàm số bậc hai
I. Hàm số bậc hai
+ Định nghĩa:
Hàm số bậc hai là hàm số cho bằng công thức dạng \(y = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R};a \ne 0.\)
+ Tập xác định: \(\mathbb{R}\)
II. Đồ thị hàm số bậc hai
+) Đồ thị hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) \((a \ne 0)\) là một parabol (P):
- Đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
- Trục đối xứng: đường thẳng \(x = - \frac{b}{{2a}}\)
- Bề lõm: quay lên trên nếu \(a > 0\), quay xuống dưới nếu \(a < 0\)
- Cắt Oy tại điểm \((0;c)\)
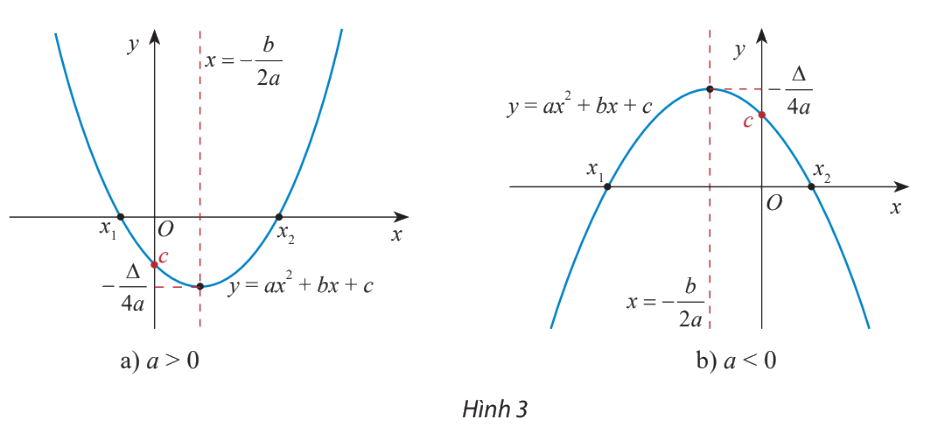
* Chú ý: Nếu PT \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) thì đồ thị hàm số \(y = a{x^2} + bx + c\) cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.
+) Vẽ đồ thị
1) Xác định đỉnh \(S\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
2) Vẽ trục đối xứng d: \(x = - \frac{b}{{2a}}\)
3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).
Xác định \(B\left( {\frac{{ - b}}{a};c} \right)\) (là điểm đối xứng với A qua d)
4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.
III. Ứng dụng
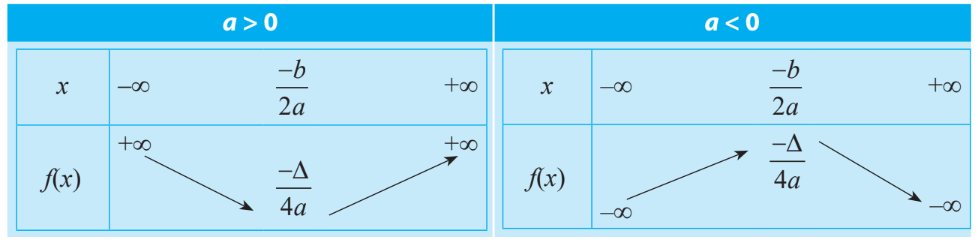
+) Bảng biến thiên
+) Ứng dụng của hàm số bậc hai
Hàm số bậc hai là một trong những khái niệm cơ bản và quan trọng trong đại số, đặc biệt là trong chương trình Toán 10. Bài viết này sẽ trình bày chi tiết về lý thuyết hàm số bậc hai, đồ thị hàm số bậc hai và các ứng dụng của nó, dựa trên nội dung sách giáo khoa Toán 10 Cánh diều.
Hàm số bậc hai có dạng tổng quát: y = ax2 + bx + c, trong đó a, b, c là các số thực và a ≠ 0. 'a' là hệ số bậc hai, 'b' là hệ số bậc nhất và 'c' là hệ số tự do.
Tập xác định của hàm số bậc hai là tập hợp tất cả các số thực, ký hiệu là ℝ. Điều này có nghĩa là hàm số bậc hai có thể nhận bất kỳ giá trị nào của x.
Đồ thị của hàm số bậc hai là một đường cong được gọi là parabol. Hình dạng của parabol phụ thuộc vào dấu của hệ số 'a':
Đỉnh của parabol là điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) trên đồ thị. Tọa độ đỉnh (x0, y0) được tính như sau:
Trục đối xứng của parabol là đường thẳng đi qua đỉnh và song song với trục Oy. Phương trình của trục đối xứng là x = x0.
Bảng biến thiên giúp ta hình dung sự thay đổi của hàm số khi x thay đổi. Việc lập bảng biến thiên bao gồm xác định đỉnh, trục đối xứng và một số điểm đặc biệt trên đồ thị.
Hàm số bậc hai có nhiều ứng dụng trong thực tế, bao gồm:
Ví dụ 1: Xác định đỉnh và trục đối xứng của hàm số y = 2x2 - 8x + 6.
Giải:
Ví dụ 2: Vẽ đồ thị của hàm số y = x2 - 4x + 3.
Giải:
Hi vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết hàm số bậc hai, đồ thị hàm số bậc hai và các ứng dụng của nó trong chương trình Toán 10 Cánh diều. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.