Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục I trang 12 và 13 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hãy nêu cách cho một tập hợp. Người ta còn minh họa tập hợp bằng một vòng kín, Nêu số phần tử của mỗi tập hợp sau
Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp.
Lời giải chi tiết:
Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}
Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Nêu số phần tử của mỗi tập hợp sau:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} ,\) \(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} \). Tập hợp G không chứa phần tử nào vì \({x^2} - 2 = 0 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb{Z}\)
\(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\): tập hợp N* có vô số phần tử.
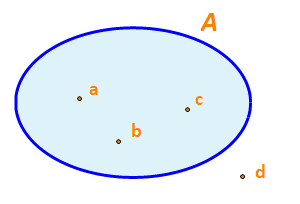
Người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Phương pháp giải:
a) Liệt kê các phần tử biểu thị bởi chấm bên trong vòng kín.
b) Xác định các phần tử không thuộc A (các chấm bên ngoài vòng kín)
Lời giải chi tiết:
a) Tập hợp A là: A = {a; b; c}
b) Phần tử không thuộc tập hợp A là: d.
Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp.
Lời giải chi tiết:
Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}
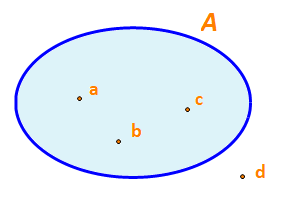
Người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Phương pháp giải:
a) Liệt kê các phần tử biểu thị bởi chấm bên trong vòng kín.
b) Xác định các phần tử không thuộc A (các chấm bên ngoài vòng kín)
Lời giải chi tiết:
a) Tập hợp A là: A = {a; b; c}
b) Phần tử không thuộc tập hợp A là: d.
Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Nêu số phần tử của mỗi tập hợp sau:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} ,\) \(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\)
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải chi tiết:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} \). Tập hợp G không chứa phần tử nào vì \({x^2} - 2 = 0 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb{Z}\)
\(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\): tập hợp N* có vô số phần tử.
Mục I trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc giới thiệu các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức toán học phức tạp hơn trong các chương sau. Việc nắm vững nội dung của mục I là điều kiện cần thiết để giải quyết các bài tập liên quan một cách hiệu quả.
Mục I bao gồm các nội dung chính sau:
Dưới đây là lời giải chi tiết cho từng bài tập trong mục I trang 12 và 13 SGK Toán 10 tập 1 - Cánh diều:
Nội dung: Liệt kê các phần tử của các tập hợp sau: A = {x | x là số tự nhiên nhỏ hơn 10}; B = {x | x là số chẵn nhỏ hơn 10}; C = {x | x là số nguyên tố nhỏ hơn 10}.
Lời giải:
Nội dung: Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Lời giải:
Nội dung: Cho tập hợp A = {1, 2, 3}. Tìm tập hợp B sao cho B ⊂ A.
Lời giải:
Có nhiều tập hợp B thỏa mãn điều kiện B ⊂ A, ví dụ:
Để giải các bài tập về tập hợp một cách hiệu quả, các em cần:
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học khác, như:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em đã hiểu rõ hơn về nội dung mục I trang 12, 13 SGK Toán 10 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!