Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 98 SGK Toán 10 tập 1 – Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em giải quyết mọi khó khăn trong môn Toán.
Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 40 km/h (Hình 68). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h.)
Đề bài
Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 40 km/h (Hình 68). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h.)
Phương pháp giải - Xem chi tiết
+) Tổng hợp vecto vận tốc theo quy tắc hình bình hành: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (ABCD là hình bình hành)
+) Định lí cosin trong tam giác ABC: \(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Lời giải chi tiết
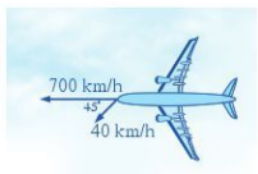
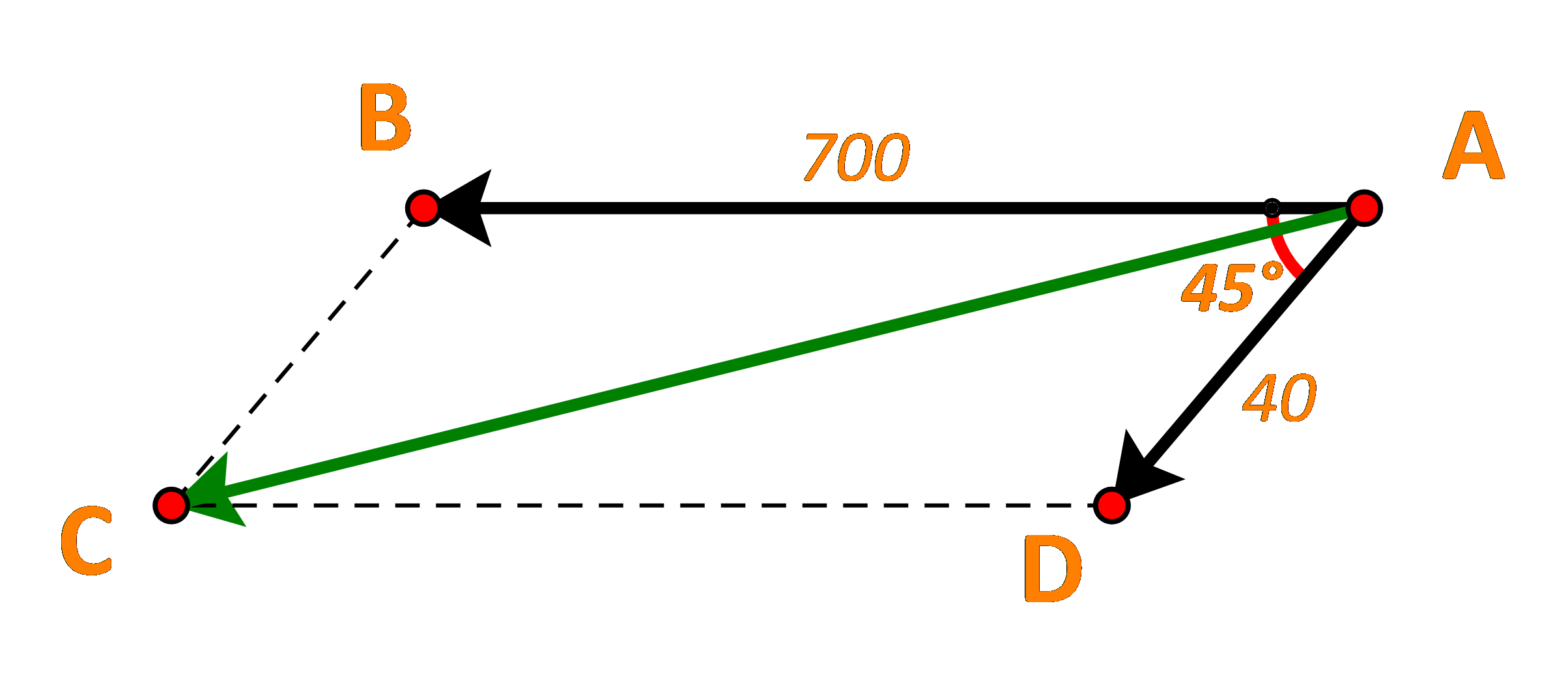
Vẽ vecto \(\overrightarrow {AB} \) là vecto vận tốc của máy bay, \(\overrightarrow {AD} \) là vecto vận tốc của gió.
Khi đó vecto vận tốc mới của máy bay là \(\overrightarrow {AB} + \overrightarrow {AD} \)
Dựng hình bình hành ABCD. Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Mà AB = 700, BC = AD = 40, \(\widehat B = {135^o}\)
\(\begin{array}{l} \Rightarrow A{C^2} = {700^2} + {40^2} - 2.700.40.\cos {135^o} \approx 531197,98\\ \Leftrightarrow AC \approx 728,83\end{array}\)
Vậy tốc độ mới của máy bay là 728,83 km/h.
Bài 7 trang 98 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và đặc biệt là ứng dụng của vectơ trong việc chứng minh các tính chất hình học.
Bài 7 trang 98 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 7. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày một ví dụ minh họa về cách giải một bài tập tương tự.)
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Lời giải:
Vì ABCD là hình bình hành nên overrightarrow{AC} =overrightarrow{AB} +overrightarrow{AD}. Mặt khác, vì M là trung điểm của BC nên overrightarrow{BM} = (1/2)overrightarrow{BC}. Do overrightarrow{BC} =overrightarrow{AD} (vì ABCD là hình bình hành) nên overrightarrow{BM} = (1/2)overrightarrow{AD}.
Ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM} =overrightarrow{AB} + (1/2)overrightarrow{AD}. Thay overrightarrow{AD} =overrightarrow{AC} -overrightarrow{AB} vào, ta được:
overrightarrow{AM} =overrightarrow{AB} + (1/2)(overrightarrow{AC} -overrightarrow{AB}) =overrightarrow{AB} + (1/2)overrightarrow{AC} - (1/2)overrightarrow{AB} = (1/2)overrightarrow{AB} + (1/2)overrightarrow{AC} = (overrightarrow{AB} +overrightarrow{AC})/2.
Vậy, overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và các mẹo giải bài tập vectơ trên, các em sẽ tự tin hơn khi giải bài 7 trang 98 SGK Toán 10 tập 1 – Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!