Chào mừng bạn đến với bài học lý thuyết Khái niệm vectơ trong chương trình Toán 10 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về vectơ, một khái niệm nền tảng trong hình học và vật lý.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa vectơ, các yếu tố của vectơ, các phép toán trên vectơ và ứng dụng của vectơ trong giải quyết các bài toán thực tế.
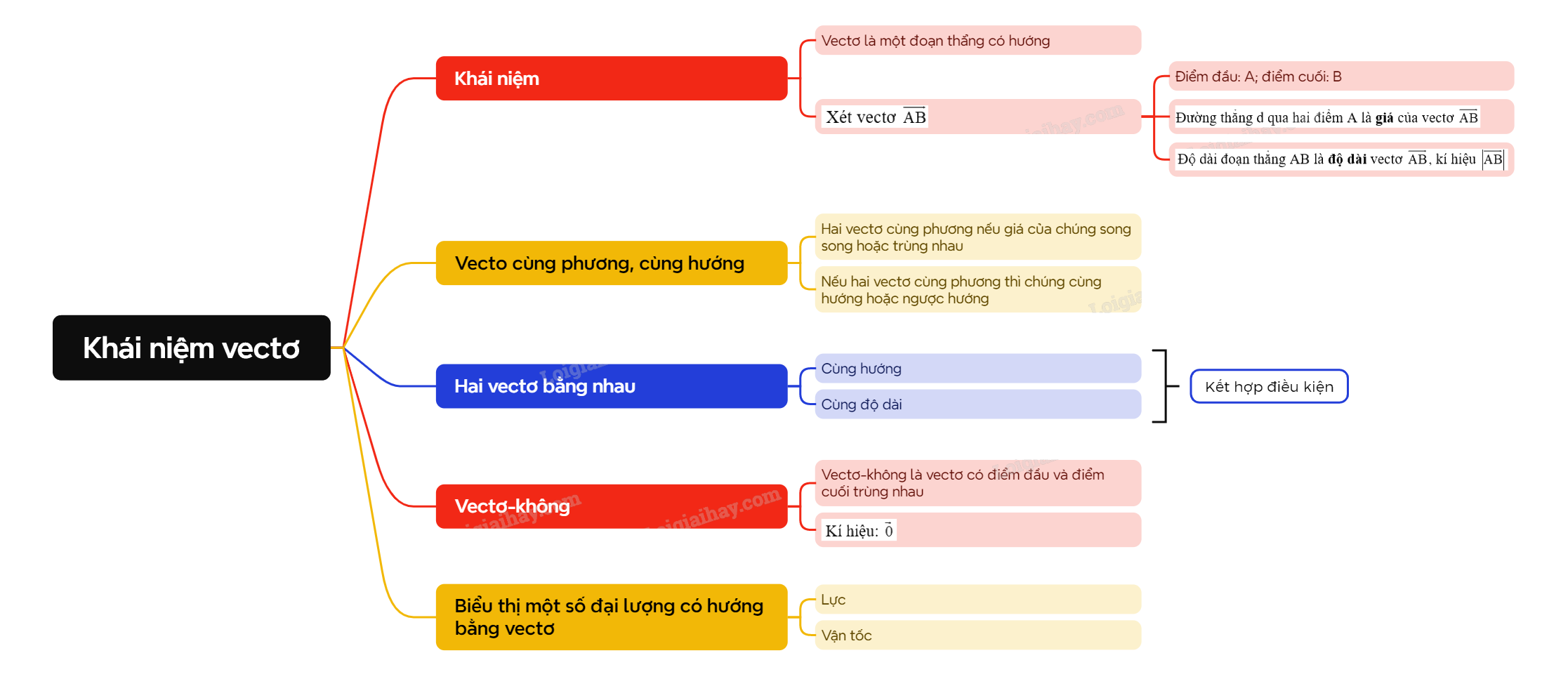
A. Lý thuyết 1. Khái niệm vectơ
A. Lý thuyết
1. Khái niệm vectơ
| Vectơ là một đoạn thẳng có hướng. |
Xét vectơ \(\overrightarrow {AB} \):
- Điểm đầu: A; điểm cuối: B.
- Cách vẽ: Vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B.

- Đường thẳng d qua hai điểm A là giá của vectơ \(\overrightarrow {AB} \).
- Độ dài đoạn thẳng AB là độ dài vectơ \(\overrightarrow {AB} \), kí hiệu \(\left| {\overrightarrow {AB} } \right|\).

Khi không cần chỉ rõ điểm đầu và điểm cuối, vectơ còn được kí hiệu là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow u ,\overrightarrow v ,...\) Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
2. Vecto cùng phương, vectơ cùng hướng.
| Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. |
Ví dụ: Các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {CD} \) và \(\overrightarrow {PQ} \) cùng phương (hình vẽ).
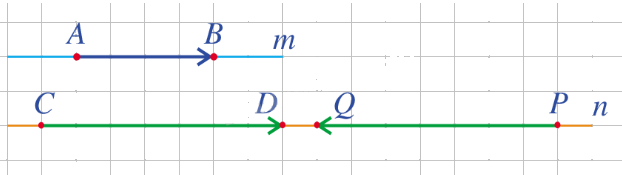
Nhận xét: Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
3. Hai vectơ bằng nhau
| Hai vectơ \(\overrightarrow {AB} \), \(\overrightarrow {CD} \) bằng nhau nếu chúng cùng hướng và cùng độ dài. Kí hiệu: \(\overrightarrow {AB} = \overrightarrow {CD} \). |
Nhận xét:
- Hai vectơ \(\overrightarrow a ,\overrightarrow b \) bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu \(\overrightarrow a = \overrightarrow b \).
- Khi cho trước vectơ \(\overrightarrow a \) và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho \(\overrightarrow {OA} = \overrightarrow a \).
4. Vectơ-không
| Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là \(\overrightarrow 0 \). |
Quy ước: \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vectơ và \(\left| {\overrightarrow 0 } \right| = 0\). Có thể coi mọi vectơ-không đều bằng nhau và \(\overrightarrow 0 = \overrightarrow {AA} = \overrightarrow {BB} = ...\) với mọi điểm A, B,…
Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow 0 \).
5. Biểu thị một số đại lượng có hướng bằng vectơ
Trong vật lí, một số đại lượng như: lực, vận tốc, … là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng có hướng đó, chẳng hạn: Một lực \(\overrightarrow F \) tác động lên xe tại điểm đặt A; lực \(\overrightarrow F \) có phương nằm ngang, hướng từ trái sang phải và cường độ là 40 N. Ta biểu thị lực \(\overrightarrow F \) bằng vectơ \(\overrightarrow {AB} \) như hình vẽ.
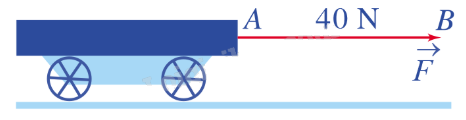
B. Bài tập
Bài 1: Cho hai điểm phân biệt H, K. Viết các vectơ (có điểm đầu khác điểm cuối) mà hai đầu mút của mỗi vectơ là hai điểm đã cho.
Giải:
Hai vectơ thoả mãn yêu cầu đề bài là \(\overrightarrow {HK} \) và \(\overrightarrow {KH} \).
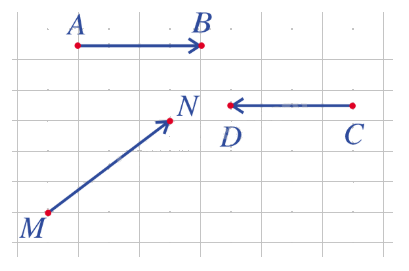
Bài 2: Tính độ dài của các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {CD} \) và \(\overrightarrow {MN} \) ở hình vẽ, biết rằng độ dài cạnh của ô vuông bằng 1 cm.
Giải:
\(\left| {\overrightarrow {AB} } \right| = 4\) cm, \(\left| {\overrightarrow {CD} } \right| = 4\) cm.
\(\left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {4^2}} = 5\) cm.
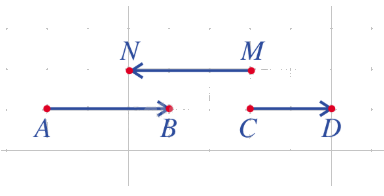
Bài 3: Trong hình vẽ, tìm vectơ cùng hướng với vectơ \(\overrightarrow {AB} \), ngược hướng với vectơ \(\overrightarrow {AB} \).
Giải:
Vectơ \(\overrightarrow {CD} \) cùng hướng với vectơ \(\overrightarrow {AB} \), vectơ \(\overrightarrow {MN} \) ngược hướng với vectơ \(\overrightarrow {AB} \).
Bài 4: Cho hình bình hành ABCD.
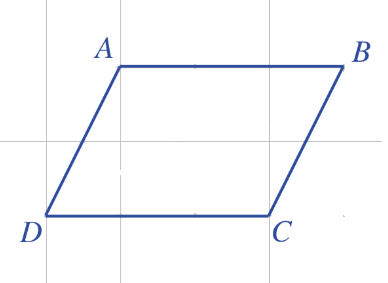
a) Vectơ nào bằng vectơ \(\overrightarrow {AB} \)?
b) Vectơ nào bằng vectơ \(\overrightarrow {AD} \)?
Giải:
a) Vì \(\overrightarrow {AB} ,\overrightarrow {DC} \) cùng hướng và AB = DC nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
b) Vì \(\overrightarrow {AD} ,\overrightarrow {BC} \) cùng hướng và AD = BC nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
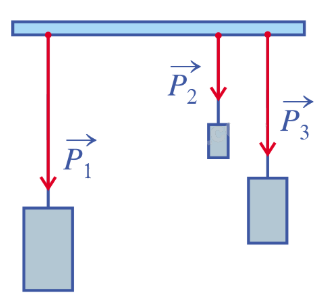
Bài 5: Khi treo ba vật lên thanh bằng những đoạn dây mảnh, không dãn, khối lượng không đáng kể, mỗi vật sẽ tác dụng lên thanh treo một lực (bằng trọng lượng của vật) như hình vẽ. Nhận xét đặc điểm về phương, hướng của ba vectơ biểu thị ba lực tác dụng lên thanh treo nói trên.
Giải:
Ba vectơ \(\overrightarrow {{P_1}} ,\overrightarrow {{P_2}} ,\overrightarrow {{P_3}} \) biểu thị ba lực tác dụng lên thanh treo là có cùng hướng.
Vectơ là một khái niệm quan trọng trong toán học, đặc biệt là trong hình học và vật lý. Hiểu rõ về vectơ là nền tảng để giải quyết nhiều bài toán liên quan đến chuyển động, lực và các đại lượng vật lý khác.
Một vectơ là một đoạn thẳng có hướng. Nó được xác định bởi độ dài và hướng. Vectơ thường được ký hiệu bằng một chữ cái in hoa hoặc một cặp chữ cái in thường có mũi tên trên đầu, ví dụ: AB hoặc a.
Một vectơ AB được xác định bởi:
Hai vectơ được gọi là:
Hai vectơ a và b được gọi là bằng nhau (a = b) nếu chúng có cùng độ dài và cùng hướng.
Một vectơ có độ dài bằng 0 được gọi là vectơ không, ký hiệu là 0. Vectơ không không có hướng xác định.
Phép cộng và trừ vectơ được thực hiện theo quy tắc hình bình hành hoặc quy tắc tam giác.
Phép trừ vectơ a - b được định nghĩa là a + (-b), trong đó -b là vectơ ngược chiều với b và có cùng độ dài.
Phép nhân vectơ a với một số thực k (k ≠ 0) được ký hiệu là ka. Vectơ ka có:
Vectơ được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về khái niệm vectơ và các tính chất cơ bản của nó. Hãy luyện tập thêm các bài tập để nắm vững kiến thức này nhé!