Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 53 SGK Toán 10 tập 2 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
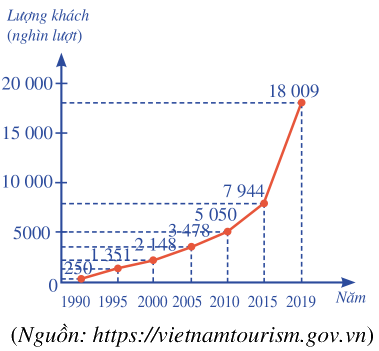
Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).
Đề bài
Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).
a) Viết mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên.
b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.
c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
a) Quan sát biểu đồ
b) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
Bước 2: Số trung bình cộng : \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
Bước 3: Trung vị \({Q_2} = {M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
c) Khoảng biến thiên: \(R = {X_n} - {X_1}\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
d) Tính phương sai \({s^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
Độ lệch chuẩn \(s = \sqrt {{s^2}} \)
Lời giải chi tiết
a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:
250 1351 2148 3478 5050 7944 18009
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)
- Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)
c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 18009 - 250 = 17759\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 7944 - 1351 = 6593\)
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {250 - \overline x } \right)}^2} + {{\left( {351 - \overline x } \right)}^2} + ... + {{\left( {18009 - \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)
Bài 3 trong SGK Toán 10 tập 2 – Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ, các phép toán cộng, trừ vectơ, phép nhân vectơ với một số thực để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và quy tắc này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Bài 3 bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập, chúng ta sẽ đi vào giải chi tiết từng câu hỏi trong bài 3:
Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Giải:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
Cho hai vectơ u = (2; -1) và v = (0; 3). Tính 2u - v.
Giải:
2u - v = 2(2; -1) - (0; 3) = (4; -2) - (0; 3) = (4 - 0; -2 - 3) = (4; -5)
Để giải tốt các bài tập về vectơ, các em cần:
Ví dụ 1: Cho A(1; 2), B(3; 4), C(5; 6). Chứng minh A, B, C thẳng hàng.
Giải:
Ta có AB = (3 - 1; 4 - 2) = (2; 2) và AC = (5 - 1; 6 - 2) = (4; 4).
Vì AC = 2AB nên ba điểm A, B, C thẳng hàng.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 3 trang 53 SGK Toán 10 tập 2 – Cánh diều là một bài tập quan trọng giúp các em hiểu rõ hơn về vectơ và các phép toán trên vectơ. Hy vọng với lời giải chi tiết và phương pháp giải bài tập mà chúng tôi cung cấp, các em sẽ học tốt môn Toán và đạt kết quả cao trong các kỳ thi.
Chúc các em học tập tốt!