Chào mừng bạn đến với bài học lý thuyết quan trọng trong chương trình Toán 10 Cánh diều: Quy tắc cộng, Quy tắc nhân và ứng dụng của Sơ đồ hình cây. Đây là những công cụ cơ bản giúp giải quyết các bài toán đếm, xác suất một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các ví dụ minh họa sinh động, giúp bạn nắm vững kiến thức và áp dụng thành thạo vào giải bài tập.
A. Lý thuyết 1. Quy tắc cộng
A. Lý thuyết
1. Quy tắc cộng
| Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành. |
2. Quy tắc nhân
| Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai thì công việc đó có m.n cách hoàn thành. |
3. Sơ đồ hình cây
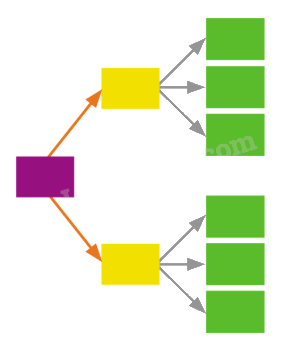
Nhận xét:
+) Sơ đồ hình cây là sơ đồ bắt đầu tại một nút duy nhất với các nhánh tỏa ra các nút bổ sung.
+) Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.
4. Vận dụng trong bài toán đếm
Việc kiên đếm có ý nghĩa quan trọng trong toán học và thực tiễn, đặc biệt trong thống kê và xác suất. Kết quả đếm cho phép chứng ta xác định được số các khả năng mà một sự kiện có thể xảy ra để làm cơ sở cho việc đưa ra quyết định. Quy tắc cộng, quy tắc nhân và sơ đồ hình cây là những nguyên tắc cơ bản trong các bài toán đếm.
a) Vận dụng trong giải toán
b) Vận dụng trong thực tiễn
B. Bài tập
Bài 1: Bạn Phương có 7 quyển sách Tiếng Anh và 8 quyển sách Văn học, các quyển sách là khác nhau. Hỏi bạn Phương có bao nhiêu cách chọn một quyển sách để đọc?
Giải:
Việc chọn một quyển sách để đọc là thực hiện một trong hai hành động sau:
Chọn một quyển sách Tiếng Anh: Có 7 cách chọn.
Chọn một quyển sách Văn học: Có 8 cách chọn.
Vậy có 7 + 8 = 15 cách chọn một quyển sách để đọc.
Bài 2: Trong kinh doanh nhà hàng, combo là một hình thức gọi món theo thực đơn được kết hợp từ nhiều món ăn hoặc đồ uống. Nếu nhà hàng có 5 món rau, 4 món cá và 3 món thịt thì có bao nhiêu cách tạo ra một combo? Biết mỗi combo có đầy đủ 1 món rau, 1 món cá và 1 món thịt.
Giải:
Để tạo một combo, ta thực hiện ba hành động liên tiếp: chọn 1 món rau, chọn 1 món cá và chọn 1 món thịt.
Chọn 1 món rau: Có 5 cách chọn.
Chọn 1 món cá: Có 4 cách chọn.
Chọn 1 món thịt: Có 3 cách chọn.
Vậy có 5.4.3 = 60 cách tạo ra một combo.
Bài 3: Bạn Hương có 3 chiếc quần khác màu: xám, đen, nâu nhạt và 4 chiếc áo sơ mi khác màu: hồng, vàng, xanh, tím. Hãy vẽ sơ đồ hình cây biểu thị số cách chọn:
a) 1 chiếc quần.
b) 1 chiếc áo sơ mi.
c) 1 bộ quần áo.
Giải:
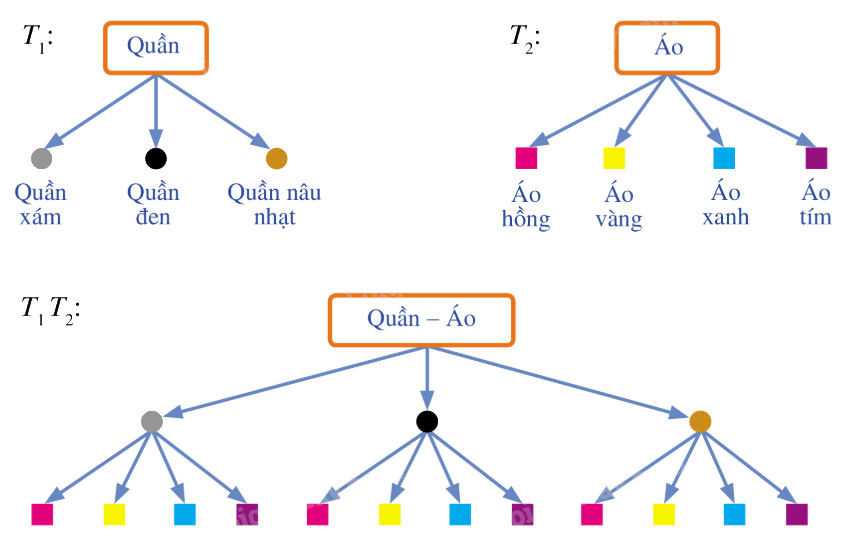
Các sơ đồ hình cây \({T_1},{T_2},{T_1}{T_2}\) trong hình vẽ lần lượt:
a) Biểu thị số cách chọn 1 chiếc quần.
b) Biểu thị số cách chọn 1 chiếc áo sơ mi.
c) Biểu thị số cách chọn 1 bộ quần áo.
Bài 4: Cho 10 điểm phân biệt. Hỏi lập được bao nhiêu vectơ khác 0? Biết rằng hai đầu mút của mỗi vectơ là 2 trong 10 điểm đã cho.
Giải:
Việc lập vectơ là thực hiện hai hành động liên tiếp: chọn điểm đầu và chọn điểm cuối.
Chọn điểm đầu: Có 10 cách chọn. Chọn điểm cuối: Có 9 cách chọn. Theo quy tắc nhân, số vectơ lập được là: 10.9 = 90.
Bài 5: Đội văn nghệ của lớp 10B có 3 học sinh nữ và 2 học sinh nam. Giáo viên chủ nhiệm muốn chọn ra một đội tam ca gồm 3 học sinh sao cho có cả học sinh nam và học sinh nữ. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn ra một đội tam ca như vậy?
Giải:
Khi chọn ra một đội tam ca gồm 3 học sinh có cả nam và nữ, giáo viên chủ nhiệm chỉ có thể chọn theo một trong hai khả năng.
* Xét khả năng thứ nhất: Chọn ra một học sinh nữ và hai học sinh nam.
- Có 3 cách chọn ra một học sinh nữ.
- Có 1 cách chọn ra hai học sinh nam.
Theo quy tắc nhân, số cách chọn ra một sinh nữ và hai học sinh nam là: 3.1 = 3.
* Xét khả năng thứ hai: Chọn ra hai học sinh nữ và một học sinh nam.
- Có 3 cách chọn ra hai học sinh nữ.
- Có 2 cách chọn ra một học sinh nam.
Theo quy tắc nhân, số cách chọn ra hai học sinh nữ và một học sinh nam là: 3.2 = 6.
Vậy theo tác cộng, số cách chọn ra một đội tam ca gồm 3 học sinh sao cho có cả học sinh nam và học sinh nữ cùng tham gia là: 3 + 6 = 9.
Bài 6: Cho kiểu gen AaBbDdEE. Giả sử quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến.
a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.
b) Từ đó, tính số loại giao tử của kiểu gen AaBbDdEE.
Giải:
a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
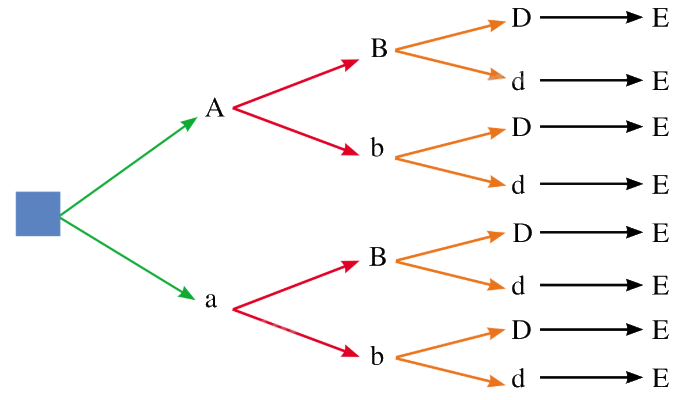
b) Từ sơ đồ hình cây, ta có 8 loại giao tử của kiểu gen AaBbDdEE.
Trong chương trình Toán 10, Quy tắc cộng, Quy tắc nhân và Sơ đồ hình cây là những công cụ đếm cơ bản, đóng vai trò quan trọng trong việc giải quyết các bài toán liên quan đến tổ hợp, xác suất. Việc nắm vững các quy tắc này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Quy tắc cộng được sử dụng khi một sự kiện có thể xảy ra theo nhiều cách khác nhau, không đồng thời. Nếu có m cách thực hiện công việc A và n cách thực hiện công việc B, thì số cách thực hiện hoặc công việc A hoặc công việc B là m + n.
Ví dụ: Một học sinh có 3 chiếc áo sơ mi và 2 chiếc quần. Hỏi học sinh đó có bao nhiêu cách chọn một bộ quần áo?
Giải: Học sinh có 3 cách chọn áo và 2 cách chọn quần. Vậy tổng số cách chọn một bộ quần áo là 3 + 2 = 5 cách.
Quy tắc nhân được sử dụng khi một sự kiện được thực hiện qua nhiều giai đoạn liên tiếp. Nếu có m cách thực hiện công việc A và n cách thực hiện công việc B sau khi đã thực hiện công việc A, thì số cách thực hiện cả hai công việc A và B là m x n.
Ví dụ: Một người cần đi từ thành phố A đến thành phố C, qua thành phố B. Có 2 con đường từ A đến B và 3 con đường từ B đến C. Hỏi người đó có bao nhiêu cách đi từ A đến C?
Giải: Người đó có 2 cách đi từ A đến B và 3 cách đi từ B đến C. Vậy tổng số cách đi từ A đến C là 2 x 3 = 6 cách.
Sơ đồ hình cây là một công cụ trực quan giúp liệt kê tất cả các kết quả có thể xảy ra của một thí nghiệm hoặc một quá trình. Nó đặc biệt hữu ích khi giải các bài toán đếm phức tạp.
Cách vẽ sơ đồ hình cây:
Ví dụ: Gieo một đồng xu hai lần liên tiếp. Vẽ sơ đồ hình cây để liệt kê tất cả các kết quả có thể xảy ra.
Giải:
Sơ đồ hình cây:
(Hình ảnh sơ đồ hình cây với các nhánh: N -> N, N -> S, S -> N, S -> S)
Bài 1: Một lớp học có 20 học sinh, trong đó có 12 học sinh nam và 8 học sinh nữ. Hỏi có bao nhiêu cách chọn một học sinh làm lớp trưởng?
Giải: Số cách chọn một học sinh làm lớp trưởng là 20 (12 nam + 8 nữ).
Bài 2: Một cửa hàng có 5 loại bánh khác nhau. Một khách hàng muốn mua 2 chiếc bánh khác loại. Hỏi khách hàng đó có bao nhiêu cách chọn bánh?
Giải: Khách hàng có 5 cách chọn chiếc bánh đầu tiên và 4 cách chọn chiếc bánh thứ hai. Vậy tổng số cách chọn là 5 x 4 = 20 cách. Tuy nhiên, vì thứ tự chọn không quan trọng, ta cần chia đôi kết quả: 20 / 2 = 10 cách.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Quy tắc cộng, Quy tắc nhân và Sơ đồ hình cây trong chương trình Toán 10 Cánh diều. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng thành thạo vào giải các bài toán thực tế.