Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 26 và 27 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình b) Tìm miền nghiệm của hệ bất phương trình đã cho. Biểu diễn miền nghiệm của hệ bất phương trình sau
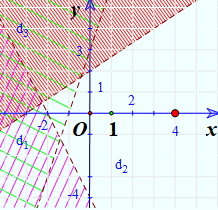
Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x - y > - 3\\ - 2x + 3y < 6\\2x + y > - 4\end{array} \right.\)
Phương pháp giải:
Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.
Lời giải chi tiết:
Vẽ đường thẳng \(3x - y = - 3\) (nét đứt)
Thay tọa độ O vào \(3x - y > - 3\) ta được \(3.0 - 0 > - 3\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \( - 2x + 3y = 6\) (nét đứt)
Thay tọa độ O vào \( - 2x + 3y < 6\) ta được \( - 2.0 + 3.0 < 6\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \(2x + y = - 4\)(nét đứt)
Thay tọa độ O vào \(2x + y > - 4\) ta được \(2.0 + 0 > - 4\) (Đúng)
Gạch đi phần không chứa O
Miền nghiệm của hệ là phần không bị gạch chéo:
Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x - 2y \ge - 2\\7x - 4y \le 16\\2x + y \ge - 4\end{array} \right.\)
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình
trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
Phương pháp giải:
a) Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.
b) Miền nghiệm của hệ là miền nghiệm chung của 3 bất phương trình.
Lời giải chi tiết:
a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x - 2y = - 2\);
\({d_2}:7x - 4y = 16\)
\({d_3}:2x + y = - 4\)
Thay tọa độ điểm O vào \(x - 2y\) ta được:
\(0 - 2.0 = 0 \ge - 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x - 4y\) ta được:
\(7.0 - 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge - 4\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
b)
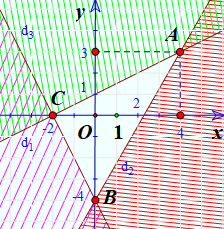
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.
Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x - 2y \ge - 2\\7x - 4y \le 16\\2x + y \ge - 4\end{array} \right.\)
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình
trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.
Phương pháp giải:
a) Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.
b) Miền nghiệm của hệ là miền nghiệm chung của 3 bất phương trình.
Lời giải chi tiết:
a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x - 2y = - 2\);
\({d_2}:7x - 4y = 16\)
\({d_3}:2x + y = - 4\)
Thay tọa độ điểm O vào \(x - 2y\) ta được:
\(0 - 2.0 = 0 \ge - 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x - 4y\) ta được:
\(7.0 - 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge - 4\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
b)
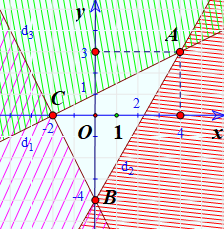
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.
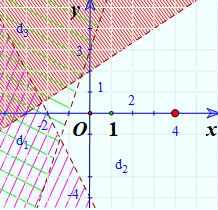
Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x - y > - 3\\ - 2x + 3y < 6\\2x + y > - 4\end{array} \right.\)
Phương pháp giải:
Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.
Lời giải chi tiết:
Vẽ đường thẳng \(3x - y = - 3\) (nét đứt)
Thay tọa độ O vào \(3x - y > - 3\) ta được \(3.0 - 0 > - 3\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \( - 2x + 3y = 6\) (nét đứt)
Thay tọa độ O vào \( - 2x + 3y < 6\) ta được \( - 2.0 + 3.0 < 6\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \(2x + y = - 4\)(nét đứt)
Thay tọa độ O vào \(2x + y > - 4\) ta được \(2.0 + 0 > - 4\) (Đúng)
Gạch đi phần không chứa O
Miền nghiệm của hệ là phần không bị gạch chéo:
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các khái niệm và bài tập liên quan đến tập hợp số thực, bao gồm các phép toán trên số thực, các tính chất của số thực, và ứng dụng của số thực trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các phần tiếp theo của môn Toán.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia, lũy thừa trên các số thực khác nhau. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán và các tính chất của phép toán trên số thực.
Bài tập này yêu cầu học sinh vận dụng các tính chất của số thực như tính giao hoán, tính kết hợp, tính chất phân phối để chứng minh các đẳng thức hoặc giải các phương trình đơn giản.
Bài tập này yêu cầu học sinh sử dụng kiến thức về số thực để giải quyết các bài toán thực tế, ví dụ như tính diện tích, chu vi, thể tích của các hình học đơn giản.
| Hình | Công thức tính diện tích |
|---|---|
| Hình vuông | S = a2 |
| Hình chữ nhật | S = a * b |
Để giải các bài tập trong mục II trang 26, 27 SGK Toán 10 tập 1 - Cánh diều một cách hiệu quả, học sinh cần:
Khi giải các bài tập về số thực, học sinh cần chú ý đến các vấn đề sau:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 10. Chúc các em học tốt và đạt kết quả cao trong kỳ thi sắp tới!