Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 61, 62, 63 sách giáo khoa Toán 10 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho điểm M trong mặt phẳng toạ độ Oxy. a) Vē vecto OM b) Nêu cách xác định toạ độ của điểm M.
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vē vecto\(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.
Lời giải chi tiết:
a) Ta có vecto \(\overrightarrow {OM}\) với điểm đầu là O và điểm cuối là M như hình 4.
b) Cách xác định tọa độ điểm M là:
• Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.
• Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.
Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy.
Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \).
Lời giải chi tiết:
Để xác định điểm A, ta làm như sau (Hình 8):
• Qua O kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow u \).
• Lấy điểm A trên đường thẳng d sao cho hai vectơ \(\overrightarrow {OA} \), \(\overrightarrow u \) cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ \(\overrightarrow u \).
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\)
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \)
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \)
Lời giải chi tiết:
a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)
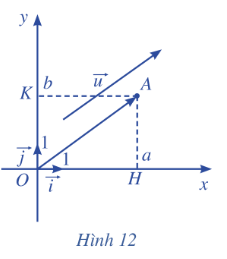
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \)
Lời giải chi tiết:
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \)( ĐPCM )
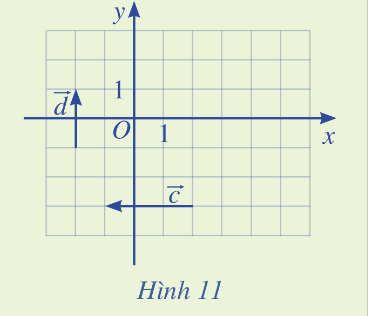
Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11
Lời giải chi tiết:
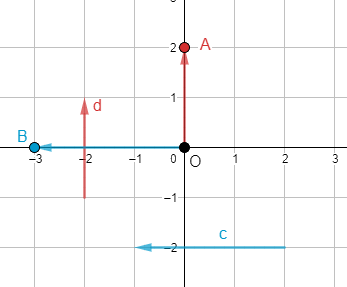
Ta vẽ vecto \(\overrightarrow {OA} = \overrightarrow d \) và \(A\left( {0;2} \right)\). Tọa độ \(\overrightarrow {OA} \) chính là tọa độ của điểm A nên \(\overrightarrow d = \left( {2;2} \right)\)
Ta vẽ vecto \(\overrightarrow {OB} = \overrightarrow c \) và \(A\left( { - 3;0} \right)\). Tọa độ \(\overrightarrow {OB} \) chính là tọa độ của điểm B nên \(\overrightarrow c = \left( { - 3;0} \right)\)
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vē vecto\(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.
Lời giải chi tiết:
a) Ta có vecto \(\overrightarrow {OM}\) với điểm đầu là O và điểm cuối là M như hình 4.
b) Cách xác định tọa độ điểm M là:
• Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.
• Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.
Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy.
Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \).
Lời giải chi tiết:
Để xác định điểm A, ta làm như sau (Hình 8):
• Qua O kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow u \).
• Lấy điểm A trên đường thẳng d sao cho hai vectơ \(\overrightarrow {OA} \), \(\overrightarrow u \) cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ \(\overrightarrow u \).
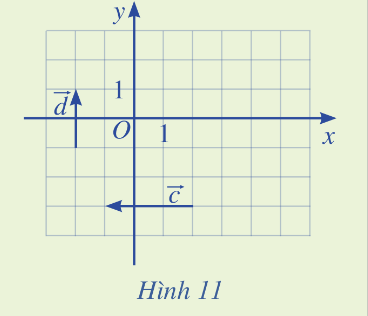
Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11
Lời giải chi tiết:
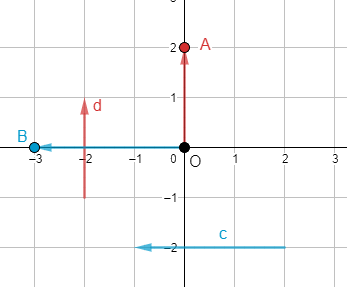
Ta vẽ vecto \(\overrightarrow {OA} = \overrightarrow d \) và \(A\left( {0;2} \right)\). Tọa độ \(\overrightarrow {OA} \) chính là tọa độ của điểm A nên \(\overrightarrow d = \left( {2;2} \right)\)
Ta vẽ vecto \(\overrightarrow {OB} = \overrightarrow c \) và \(A\left( { - 3;0} \right)\). Tọa độ \(\overrightarrow {OB} \) chính là tọa độ của điểm B nên \(\overrightarrow c = \left( { - 3;0} \right)\)
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \)
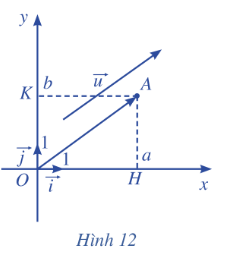
Lời giải chi tiết:
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \)( ĐPCM )
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\)
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \)
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \)
Lời giải chi tiết:
a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)
Mục II trong SGK Toán 10 tập 2 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như Vectơ trong mặt phẳng, tích vô hướng của hai vectơ, hoặc các ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức lý thuyết và kỹ năng giải bài tập trong mục này là rất quan trọng để xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục II trang 61, 62, 63, chúng ta sẽ đi vào giải chi tiết từng bài tập. Lưu ý rằng, trước khi bắt đầu giải bài tập, các em nên đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
Đề bài: (Giả định một đề bài cụ thể về vectơ)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể về tích vô hướng)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể về ứng dụng của vectơ)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập sau:
Hy vọng rằng, với lời giải chi tiết và các kiến thức bổ ích được cung cấp trong bài viết này, các em sẽ tự tin hơn trong việc giải các bài tập mục II trang 61, 62, 63 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!
| Chủ đề | Nội dung |
|---|---|
| Vectơ | Định nghĩa, phép toán |
| Tích vô hướng | Công thức, ứng dụng |
| Hình học | Ứng dụng vectơ |
| Nguồn: giaitoan.edu.vn | |