Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục I trang 73, 74 SGK Toán 10 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài tập mục I tập trung vào các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học.
Trong mặt phẳng toạ độ Oxy, cho đường thẳng Cho đường thẳng có phương trình tham số
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - 2t\\y = - 2 + t\end{array} \right.\)
a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng \(\Delta \).
b) Điểm nào trong các điểm C(-1;-1), D(1;3) thuộc đường thẳng \(\Delta \)?
Lời giải chi tiết:
a) Chọn \(t = 0;t = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {1; - 2} \right),B\left( { - 1; - 1} \right)\).
b)
+) Thay tọa độ điểm C vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}-1 = 1 - 2t\\ - 1 = - 2 + t\end{array} \right.\). Ta được t = 1. Vậy C thuộc đường thẳng \(\Delta \).
+) Thay tọa độ điểm D vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\3 = - 2 + t\end{array} \right.\). Do không có t thỏa mãn nên D không thuộc đường thẳng \(\Delta \).

Lời giải chi tiết:
Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.
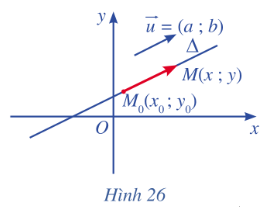
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ chỉ phương\(\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 26).
a) Nhận xét về phương của hai vectơ \(\overrightarrow u {\rm{ }}\) và \(\overrightarrow {{M_o}M} \).
b) Chứng minh có số thực t sao cho \(\overrightarrow {{M_o}M} \) = \(t\overrightarrow u {\rm{ }}\).
c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm \({M_o}\) và toạ độ của vectơ chỉ phương \(\overrightarrow u {\rm{ }}\).
Lời giải chi tiết:
a) Hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì \(\overrightarrow u \) cùng phương với \(\overrightarrow {{M_o}M} \) nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \).
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\).
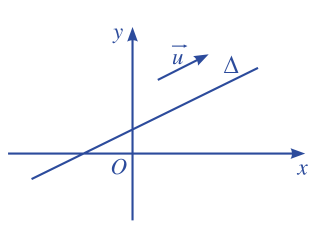
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \). Vẽ vectơ \(\overrightarrow u \) (\(\overrightarrow u \ne \overrightarrow 0 \)) có giá song song (hoặc trùng) với đường thẳng \(\Delta \).
Lời giải chi tiết:
Nhận xét
• Nếu \(\overrightarrow u \) là một vectơ chỉ phương của A thì \(k\overrightarrow u \) (\(k \ne 0\)) cũng là một vectơ chỉ phương của A.
• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.

Lời giải chi tiết:
Để xác định tọa độ của máy bay ta phải lập phương trình quỹ đạo bay của máy bay hay chính là lập phương trình đường thẳng.
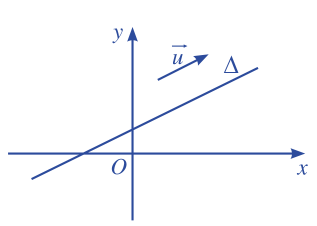
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \). Vẽ vectơ \(\overrightarrow u \) (\(\overrightarrow u \ne \overrightarrow 0 \)) có giá song song (hoặc trùng) với đường thẳng \(\Delta \).
Lời giải chi tiết:
Nhận xét
• Nếu \(\overrightarrow u \) là một vectơ chỉ phương của A thì \(k\overrightarrow u \) (\(k \ne 0\)) cũng là một vectơ chỉ phương của A.
• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.
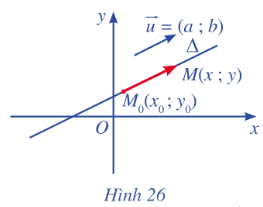
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ chỉ phương\(\overrightarrow u {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 26).
a) Nhận xét về phương của hai vectơ \(\overrightarrow u {\rm{ }}\) và \(\overrightarrow {{M_o}M} \).
b) Chứng minh có số thực t sao cho \(\overrightarrow {{M_o}M} \) = \(t\overrightarrow u {\rm{ }}\).
c) Biểu diễn toạ độ của điểm M qua toạ độ của điểm \({M_o}\) và toạ độ của vectơ chỉ phương \(\overrightarrow u {\rm{ }}\).
Lời giải chi tiết:
a) Hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Xét \(M\left( {x;y} \right)\). Vì \(\overrightarrow u \) cùng phương với \(\overrightarrow {{M_o}M} \) nên có số thực t sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \).
c) Do \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\) nên:
\(\overrightarrow {{M_o}M} = t\overrightarrow u {\rm{ }} \Leftrightarrow \left\{ \begin{array}{l}x - {x_o} = at\\y - {y_o} = bt\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {x_o} + at\\y = {y_o} + bt\end{array} \right.\)
Vậy tọa độ điểm M là: \(M\left( {{x_o} + at;{y_o} + bt} \right)\).
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - 2t\\y = - 2 + t\end{array} \right.\)
a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng \(\Delta \).
b) Điểm nào trong các điểm C(-1;-1), D(1;3) thuộc đường thẳng \(\Delta \)?
Lời giải chi tiết:
a) Chọn \(t = 0;t = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {1; - 2} \right),B\left( { - 1; - 1} \right)\).
b)
+) Thay tọa độ điểm C vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}-1 = 1 - 2t\\ - 1 = - 2 + t\end{array} \right.\). Ta được t = 1. Vậy C thuộc đường thẳng \(\Delta \).
+) Thay tọa độ điểm D vào phương trình đường thẳng \(\Delta \) ta có: \(\left\{ \begin{array}{l}1 = 1 - 2t\\3 = - 2 + t\end{array} \right.\). Do không có t thỏa mãn nên D không thuộc đường thẳng \(\Delta \).
Mục I trang 73, 74 SGK Toán 10 tập 2 - Cánh diều là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng. Để giải tốt các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản, các định lý và các phép toán liên quan đến vectơ.
Vectơ được sử dụng để biểu diễn các đại lượng vật lý như lực, vận tốc, gia tốc. Trong hình học, vectơ được sử dụng để biểu diễn các điểm, đường thẳng, mặt phẳng và các phép biến hình.
Lời giải: Theo quy tắc hình bình hành, vectơ tổng của AB và AD là vectơ AC. Do đó, AB + AD = AC.
Lời giải: a - b = a + (-b). Để tìm vectơ -b, ta chỉ cần đổi hướng của vectơ b.
Lời giải: 2a = (4; 6). 2a - b = (4; 6) - (-1; 4) = (5; 2).
Lời giải: Vì G là trọng tâm của tam giác ABC, ta có GA = 2/3 * AM, GB = 2/3 * BN, GC = 2/3 * CP, với M, N, P lần lượt là trung điểm của BC, CA, AB. Sử dụng quy tắc cộng vectơ và tính chất của trọng tâm, ta có thể chứng minh GA + GB + GC = 0.
Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin chinh phục các bài tập trong mục I trang 73, 74 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!