Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Lập phương trình đường thẳng trong các Hình 34,35,36,37:
Đề bài
Lập phương trình đường thẳng trong các Hình 34,35,36,37:
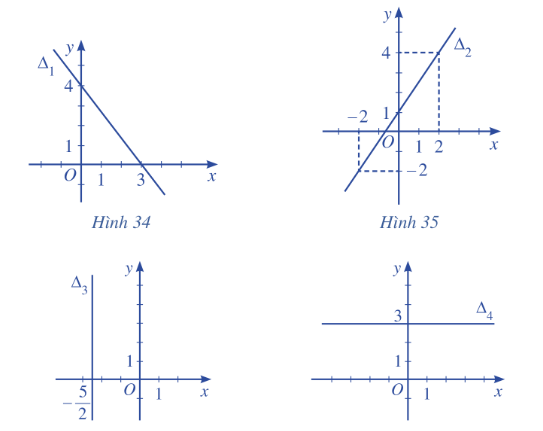
Phương pháp giải - Xem chi tiết
+) Phương trình đoạn chắn của đường thẳng d đi qua hai điểm \(A\left( {a;0} \right),B\left( {0;b} \right)\left( {ab \ne 0} \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} = 1\)
+) Phương trình đường thằng d đi qua hai điểm \(A\left( {{x_o};{y_o}} \right);B\left( {{x_1};{y_1}} \right)\) là: \(\frac{{x - {x_o}}}{{{x_1} - {x_o}}} = \frac{{y - {y_o}}}{{{y_1} - {y_o}}}\)
+) Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và nhận \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right)\)làm vecto pháp tuyến là: \(a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0\)
Lời giải chi tiết
a) Phương trình đoạn chắn của đường thẳng \({\Delta _1}\) đi qua 2 điểm \(\left( {0;4} \right)\) và \(\left( {3;0} \right)\) là: \(\frac{x}{3} + \frac{y}{4} = 1\)
b) Phương trình đường thẳng \({\Delta _2}\) đi qua 2 điểm \(\left( {2;4} \right)\) và \(\left( { - 2; - 2} \right)\) là:
\(\frac{{x - 2}}{{ - 2 - 2}} = \frac{{y - 4}}{{ - 2 - 4}} \Leftrightarrow \frac{{x - 2}}{{ - 4}} = \frac{{y - 4}}{{ - 6}} \Leftrightarrow 3x - 2y + 2 = 0\)
c) Do đường thẳng \({\Delta _3}\) vuông góc với \({\rm{O}}x\) nên vecto pháp tuyến của \({\Delta _3}\) là: \(\overrightarrow {{n_3}} = \left( {1;0} \right)\)
Vậy phương trình đường thẳng \({\Delta _3}\)đi qua điểm \(\left( { - \frac{5}{2};0} \right)\) có vecto pháp tuyến \(\overrightarrow {{n_3}} = \left( {1;0} \right)\)là: \(1\left( {x + \frac{5}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = - \frac{5}{2}\)
d) Do đường thẳng \({\Delta _4}\) vuông góc với \({\rm{O}}x\) nên vecto pháp tuyến của \({\Delta _4}\) là: \(\overrightarrow {{n_4}} = \left( {0;1} \right)\)
Vậy phương trình đường thẳng \({\Delta _4}\) đi qua điểm \(\left( {0;3} \right)\) có vecto pháp tuyến \(\overrightarrow {{n_4}} = \left( {0;1} \right)\)là: \(0\left( {x - 0} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow y = 3\)
Bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Lưu ý: Nội dung lời giải chi tiết sẽ được trình bày cụ thể cho từng câu hỏi trong bài tập, ví dụ minh họa và phân tích từng bước giải. Do giới hạn độ dài, chúng tôi sẽ cung cấp một ví dụ minh họa.)
Cho hai vectơ a = (2; 3) và b = (-1; 4). Tính tích vô hướng của a và b.
Giải:
Tích vô hướng của hai vectơ a = (x1; y1) và b = (x2; y2) được tính theo công thức:
a.b = x1x2 + y1y2
Trong trường hợp này, ta có:
a.b = (2)(-1) + (3)(4) = -2 + 12 = 10
Vậy, tích vô hướng của hai vectơ a và b là 10.
Ngoài bài 2 trang 79, SGK Toán 10 tập 2 – Cánh diều còn có nhiều bài tập tương tự. Để giải quyết các bài tập này, bạn cần nắm vững các kiến thức sau:
Để học tốt môn Toán 10, đặc biệt là phần vectơ, bạn nên:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều. Hãy luyện tập thường xuyên và áp dụng các kiến thức đã học vào thực tế để đạt kết quả tốt nhất trong môn Toán.