Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 92 SGK Toán 10 tập 1 – Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
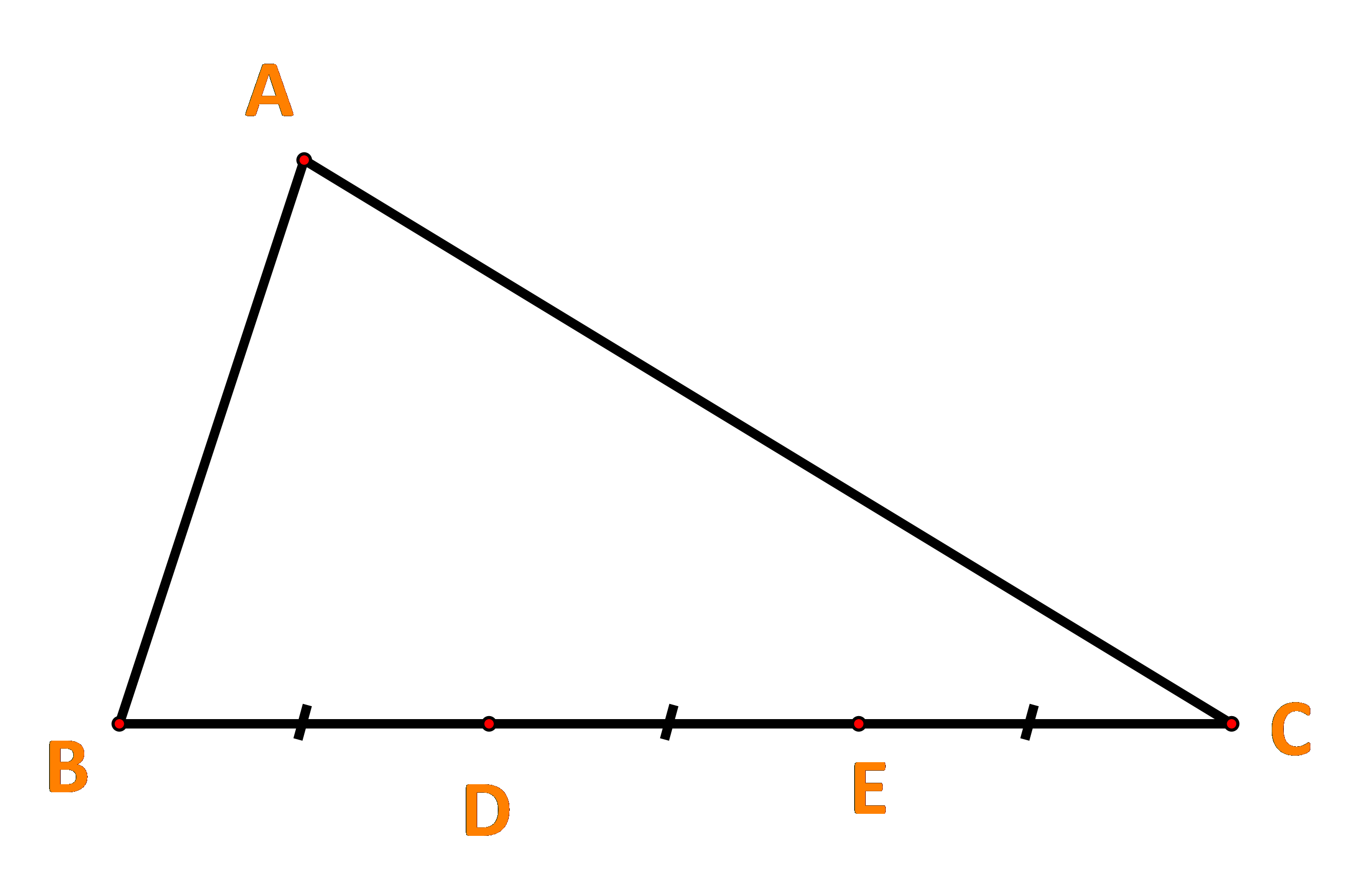
Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62).
Đề bài
Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b .\) Biểu diễn các vecto \(\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {BE} ,\overrightarrow {AD} ,\overrightarrow {AE} \) theo \(\overrightarrow a ,\overrightarrow b .\)
Phương pháp giải - Xem chi tiết
Vận dụng quy tắc cộng: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
\(\overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} \Leftrightarrow \) vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
Lời giải chi tiết
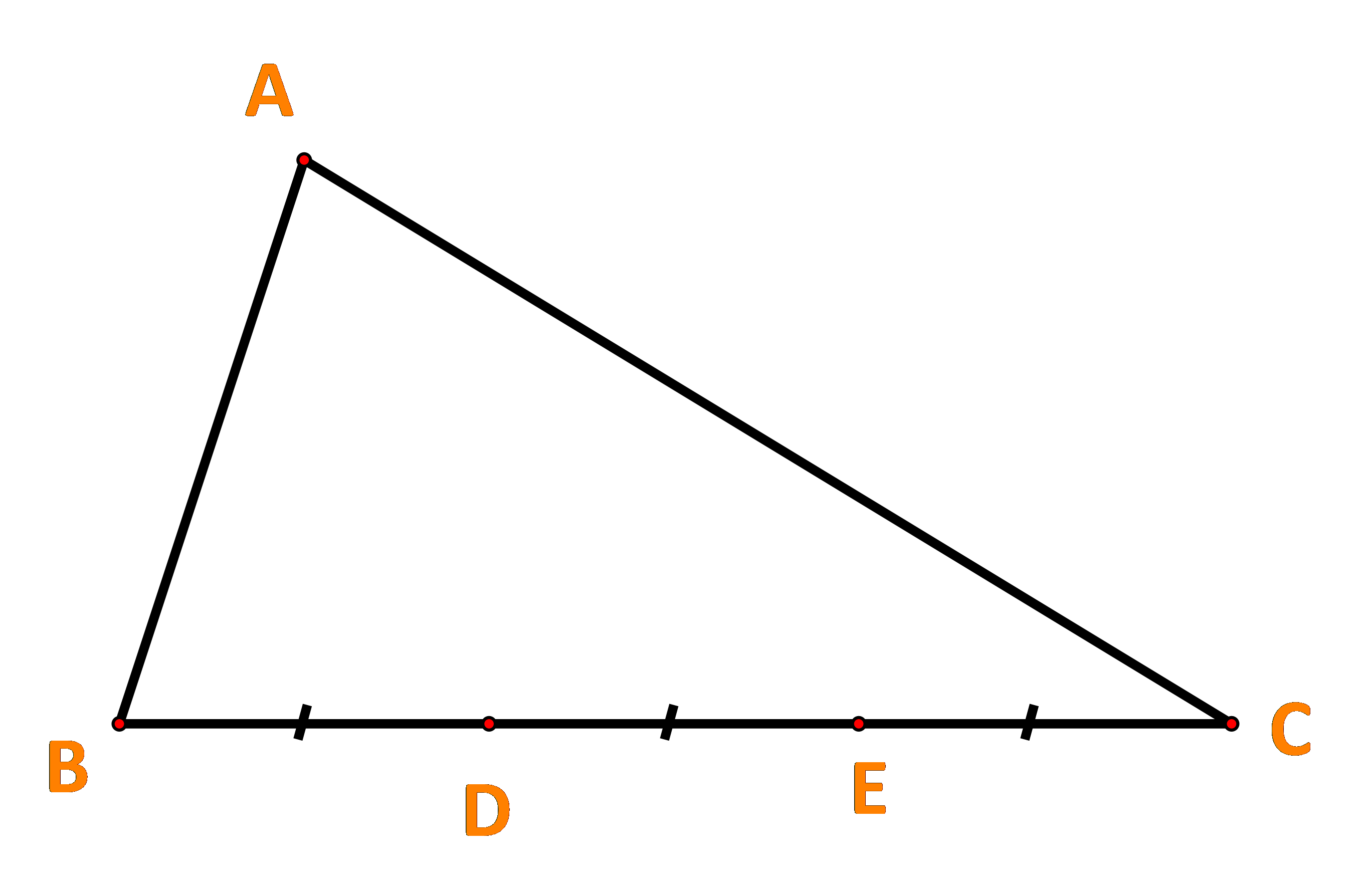
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)
Bài 4 trang 92 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học về Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, đặc biệt là phép cộng, trừ vectơ và phép nhân vectơ với một số thực để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và tính chất liên quan đến vectơ là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài 4 trang 92 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả bài 4 trang 92 SGK Toán 10 tập 1 – Cánh diều, học sinh cần:
Ví dụ 1: Cho hai vectơ a = (2; -1) và b = (-3; 4). Tính a + b.
Giải:a + b = (2 + (-3); -1 + 4) = (-1; 3)
Ví dụ 2: Cho vectơ a = (1; 2) và số thực k = -2. Tính ka.
Giải:ka = (-2 * 1; -2 * 2) = (-2; -4)
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Cánh diều và các tài liệu tham khảo khác. Ngoài ra, việc thực hành giải nhiều bài tập khác nhau sẽ giúp học sinh làm quen với các dạng bài tập và phát triển tư duy logic.
Trong quá trình học tập, nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ. Việc chủ động tìm hiểu và giải quyết các vấn đề sẽ giúp các em học tập hiệu quả hơn. Chúc các em học tốt môn Toán!
| Công thức | Mô tả |
|---|---|
| a + b = (xa + xb; ya + yb) | Phép cộng vectơ |
| a - b = (xa - xb; ya - yb) | Phép trừ vectơ |
| ka = (kxa; kya) | Phép nhân vectơ với một số thực |