Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 71 SGK Toán 10 tập 1 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc 75
Đề bài
Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc \({75^o}\). Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Bước 1: Quãng đường mỗi tàu đi được sau 2,5 giờ.
Bước 2: Tính khoảng cách giữa hai tàu bằng cách áp dụng định lí cosin.
Lời giải chi tiết
Gọi B, C lần lượt là vị trí của tàu thứ nhất và tàu thứ hai sau 2,5 giờ.
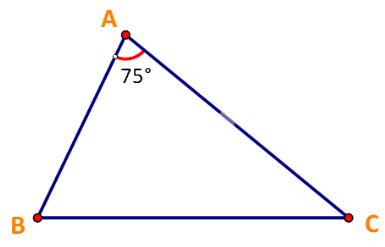
Sau 2,5 giờ:
Quãng đường tàu thứ nhất đi được là: AB = 8.2,5 = 20 (hải lí)
Quãng đường tàu thứ hai đi được là: AC = 12.2,5 = 30 (hải lí)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2.AC.AB.\cos A\)
\(\begin{array}{l} \Rightarrow B{C^2} = {30^2} + {20^2} - 2.30.20.\cos {75^o}\\ \Rightarrow B{C^2} \approx 989,4\\ \Rightarrow BC \approx 31,5\end{array}\)
Vậy hai tàu cách nhau 31,5 hải lí.
Bài 7 trang 71 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học về tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán hợp, giao, hiệu của hai tập hợp để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài 7 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A ∪ B.
Lời giải: A ∪ B = {1; 2; 3; 4; 5; 6}.
Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A ∩ B.
Lời giải: A ∩ B = {3; 4}.
Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A \ B.
Lời giải: A \ B = {1; 2}.
Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm B \ A.
Lời giải: B \ A = {5; 6}.
Để giải tốt các bài tập về tập hợp, các em cần nắm vững các khái niệm cơ bản như:
Ngoài ra, các em cũng cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau. Khi gặp một bài tập mới, các em nên:
Ví dụ 1: Cho A = {a; b; c} và B = {b; c; d}. Tìm A ∪ B.
Lời giải: A ∪ B = {a; b; c; d}.
Ví dụ 2: Cho A = {1; 2; 3} và B = {3; 4; 5}. Tìm A ∩ B.
Lời giải: A ∩ B = {3}.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ hiểu rõ hơn về bài 7 trang 71 SGK Toán 10 tập 1 – Cánh diều và tự tin hơn trong quá trình học tập môn Toán. Chúc các em học tốt!