Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 61 SGK Toán 10 tập 1 – Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em tự tin hơn trong quá trình học tập môn Toán.
Bài 6 thuộc chương trình học Toán 10 tập 1, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học cơ bản. Hãy cùng chúng tôi khám phá lời giải chi tiết và các lưu ý quan trọng để nắm vững kiến thức này nhé!
Lập bảng xét dấu của mỗi tam thức bậc hai sau
Đề bài
Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
b) \(f\left( x \right) = {x^2} - x - 12\)
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
Phương pháp giải - Xem chi tiết
Bước 1: Tìm nghiệm của \(f\left( x \right) = 0\) và hệ số a.
Bước 2: Lập bảng xét dấu.
Lời giải chi tiết
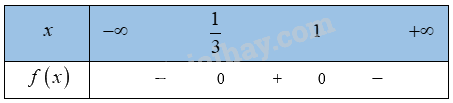
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:
b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:

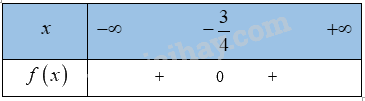
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
Bài 6 trang 61 SGK Toán 10 tập 1 – Cánh diều yêu cầu học sinh vận dụng kiến thức về vectơ để chứng minh các đẳng thức vectơ liên quan đến trung điểm, trọng tâm của tam giác. Đây là một bài tập quan trọng giúp củng cố kiến thức về vectơ và rèn luyện kỹ năng chứng minh hình học.
Bài tập 6 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để chứng minh MA = MB, ta sử dụng định nghĩa về trung điểm của đoạn thẳng. Theo định nghĩa, M là trung điểm của AB khi và chỉ khi AM = MB. Do đó, MA = MB là một khẳng định đúng.
Để chứng minh GA + GB + GC = 0, ta sử dụng định nghĩa về trọng tâm của tam giác. Trọng tâm G của tam giác ABC là giao điểm của ba đường trung tuyến. Theo tính chất của trọng tâm, ta có:
GA = 2/3 * AD, GB = 2/3 * BE, GC = 2/3 * CF, trong đó D, E, F lần lượt là trung điểm của BC, AC, AB.
Vì AD, BE, CF là các vectơ trung tuyến, ta có AD + BE + CF = 0. Từ đó suy ra GA + GB + GC = 0.
Ngoài bài tập 6, còn rất nhiều bài tập tương tự liên quan đến vectơ và ứng dụng trong hình học. Một số dạng bài tập thường gặp bao gồm:
Để giải tốt các bài tập về vectơ, các em cần nắm vững các kiến thức cơ bản sau:
Ngoài ra, các em cũng nên luyện tập thường xuyên để rèn luyện kỹ năng giải bài tập và làm quen với các dạng bài tập khác nhau.
Bài 6 trang 61 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức về vectơ và rèn luyện kỹ năng chứng minh hình học. Hy vọng với lời giải chi tiết và các lưu ý quan trọng mà chúng tôi cung cấp, các em sẽ tự tin hơn trong quá trình học tập môn Toán.
Chúc các em học tốt!