Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 61 SGK Toán 10 tập 1 – Cánh diều. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em giải quyết mọi khó khăn trong môn Toán.
Vẽ đồ thị của mỗi hàm số sau
Đề bài
Vẽ đồ thị của mỗi hàm số sau:
a) \(y = {x^2} - 3x - 4\)
b) \(y = {x^2} + 4x + 4\)
c) \(y = - {x^2} + 2x - 2\)
Phương pháp giải - Xem chi tiết
Bước 1: Xác định tọa độ đỉnh \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\)
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục \(x = - \frac{b}{{2a}}\).
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số \(y = a{x^2} + bx + c\).
Lời giải chi tiết
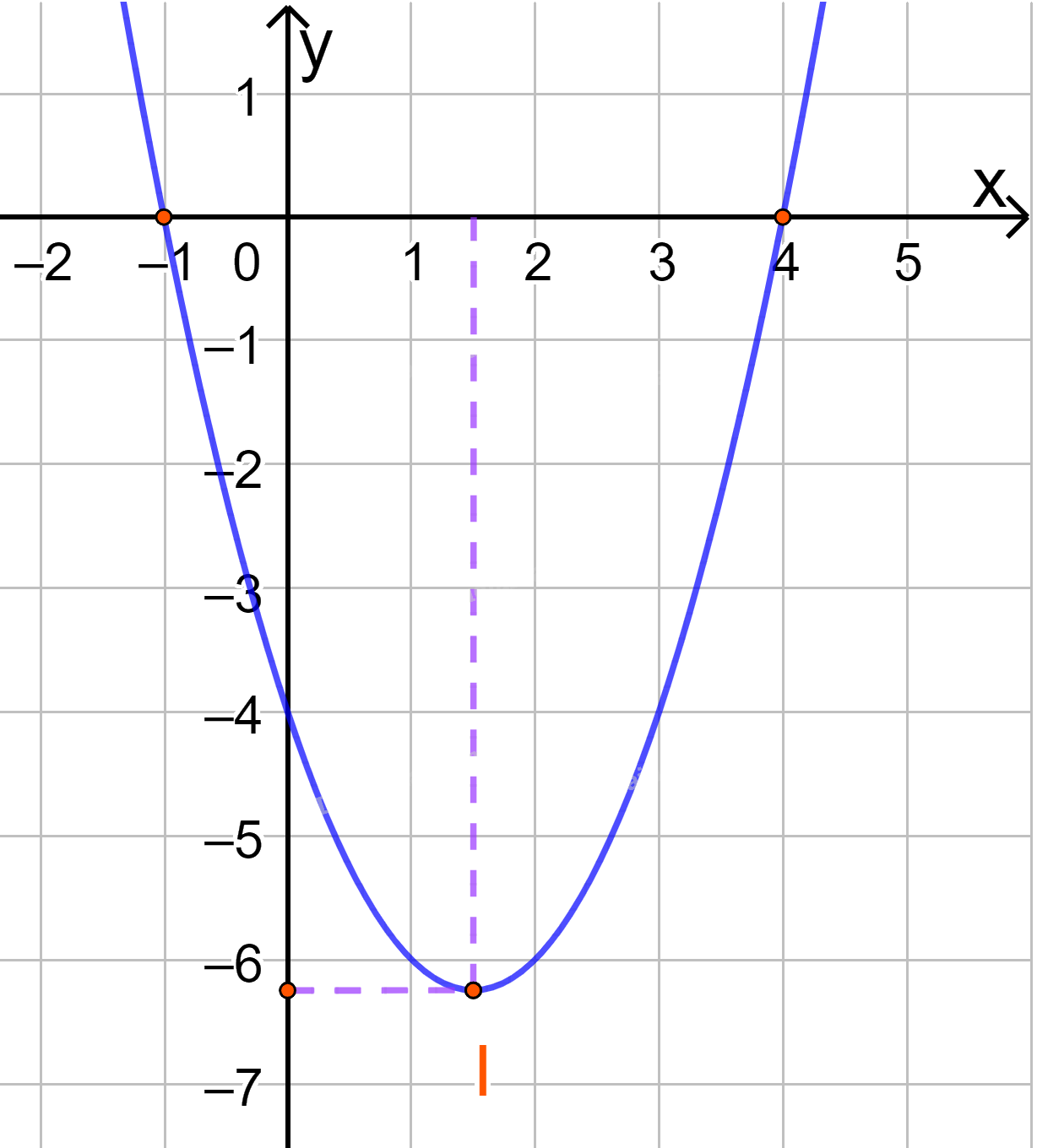
a) \(y = {x^2} - 3x - 4\)
Đồ thị hàm số có đỉnh \(I\left( {\dfrac{3}{2}; - \dfrac{{25}}{4}} \right)\)
Trục đối xứng là \(x = \dfrac{3}{2}\)
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng \(x = \frac{3}{2}\) là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
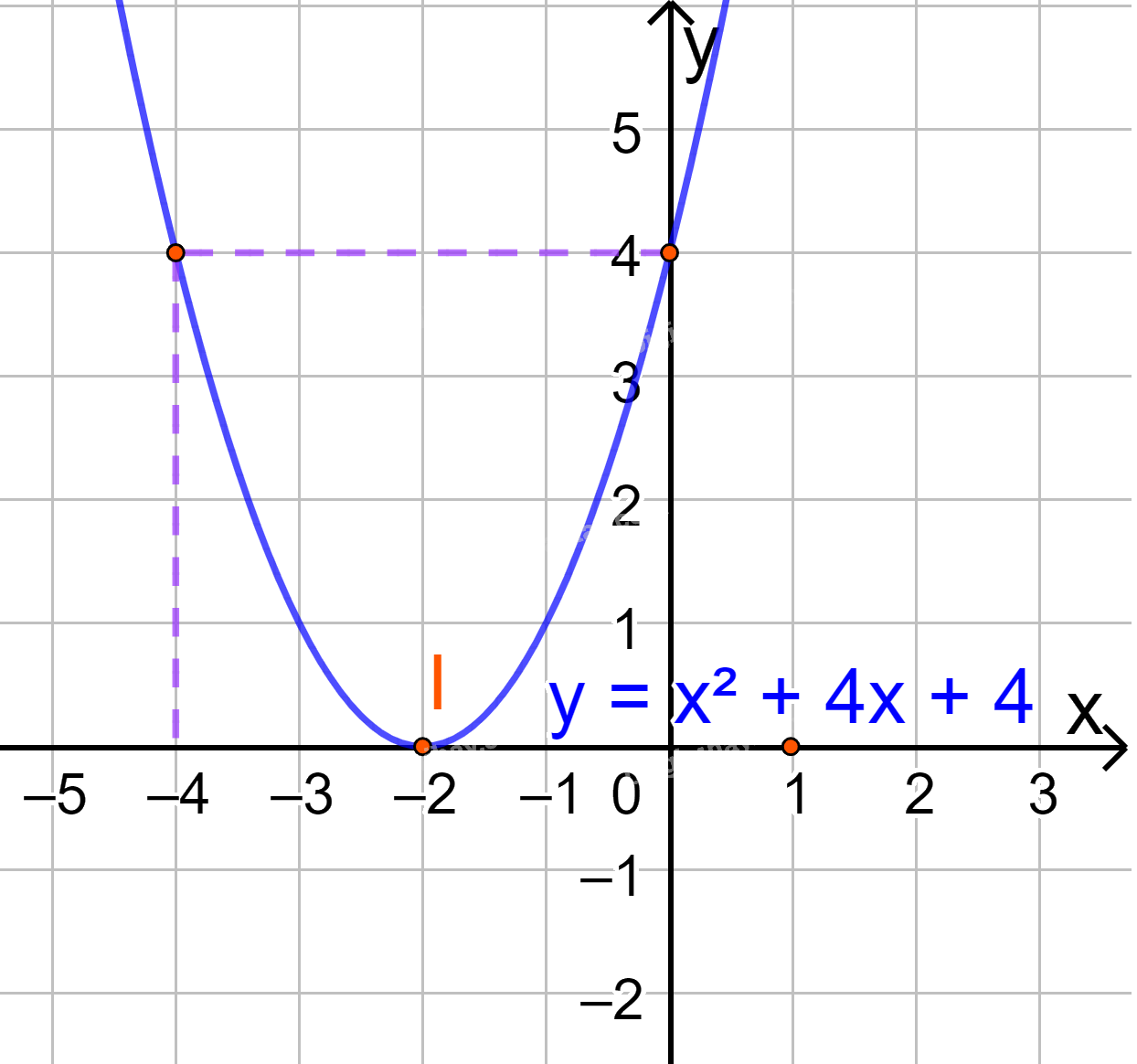
b) \(y = {x^2} + 4x + 4\)
Đồ thị hàm số có đỉnh \(I\left( { - 2;0} \right)\)
Trục đối xứng là \(x = - 2\)
Giao điểm của parabol với trục tung là (0;4)
Giao điểm của parabol với trục hoành là I(-2;0)
Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = - 2\) là (-4;4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
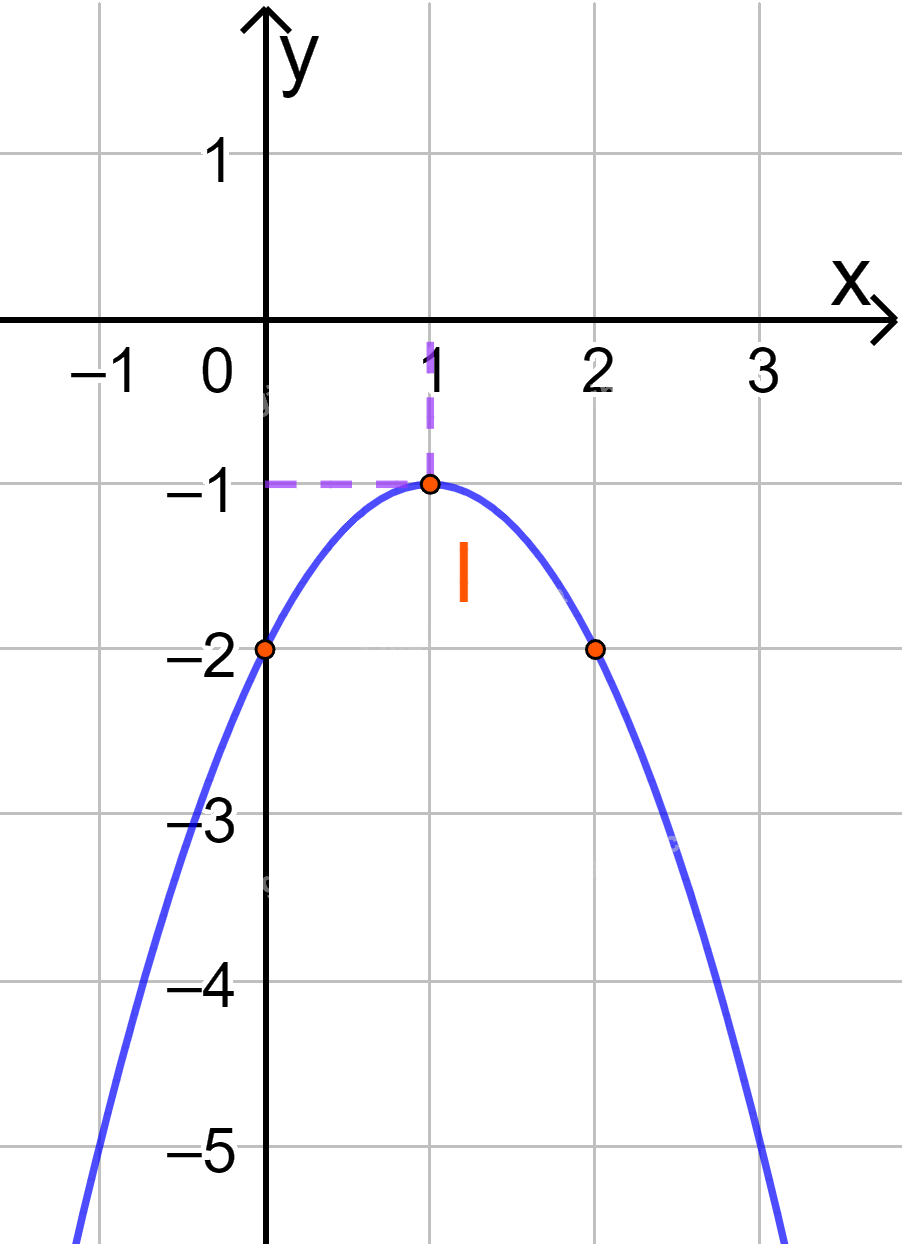
c) \(y = - {x^2} + 2x - 2\)
Đồ thị hàm số có đỉnh \(I\left( {1; - 1} \right)\)
Trục đối xứng là \(x = 1\)
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng \(x = 1\) là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Bài 5 trang 61 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất của tập hợp để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh xác định các tập hợp, tìm phần tử thuộc tập hợp, thực hiện các phép hợp, giao, hiệu, bù của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 5 bao gồm một số câu hỏi và bài tập nhỏ, mỗi câu hỏi/bài tập tập trung vào một khía cạnh khác nhau của kiến thức về tập hợp. Dưới đây là phân tích chi tiết từng phần của bài tập:
Câu a thường yêu cầu học sinh xác định các tập hợp dựa trên các điều kiện cho trước. Ví dụ, cho một tập hợp A các số tự nhiên chia hết cho 3 và nhỏ hơn 20, yêu cầu học sinh liệt kê các phần tử của tập hợp A. Để giải quyết bài toán này, học sinh cần nắm vững định nghĩa về tập hợp và các điều kiện để một phần tử thuộc tập hợp.
Câu b thường yêu cầu học sinh thực hiện các phép toán trên tập hợp, như phép hợp, giao, hiệu, bù. Ví dụ, cho hai tập hợp A và B, yêu cầu học sinh tìm tập hợp A ∪ B (hợp của A và B), A ∩ B (giao của A và B), A \ B (hiệu của A và B), và CAB (bù của B trong A). Để giải quyết bài toán này, học sinh cần nắm vững định nghĩa và công thức của các phép toán trên tập hợp.
Câu c thường yêu cầu học sinh chứng minh các đẳng thức liên quan đến tập hợp, như A ∪ B = B ∪ A, A ∩ B = B ∩ A, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Để giải quyết bài toán này, học sinh cần sử dụng các tính chất của các phép toán trên tập hợp và các quy tắc logic.
Để giải quyết các bài tập về tập hợp một cách hiệu quả, học sinh cần:
Ví dụ 1: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Tìm A ∪ B, A ∩ B, A \ B, và CAB.
Giải:
Để củng cố kiến thức về tập hợp, các em có thể tự giải các bài tập sau:
Bài 5 trang 61 SGK Toán 10 tập 1 – Cánh diều là một bài tập quan trọng giúp học sinh nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Bằng cách hiểu rõ định nghĩa, công thức, và phương pháp giải bài tập, các em có thể tự tin giải quyết mọi bài toán liên quan đến tập hợp.