Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải các bài tập trong mục I trang 93, 94 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) \(\overrightarrow {CB} .\overrightarrow {BA} \)
b) \(\overrightarrow {AH} .\overrightarrow {BC} \)
Phương pháp giải:
+) Tính tích vô hướng \(\overrightarrow {CB} .\overrightarrow {BA} \) bằng công thức \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} )\)
+) \((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} )\) nếu \(\overrightarrow {BD} = \overrightarrow {CB} \)
Lời giải chi tiết:
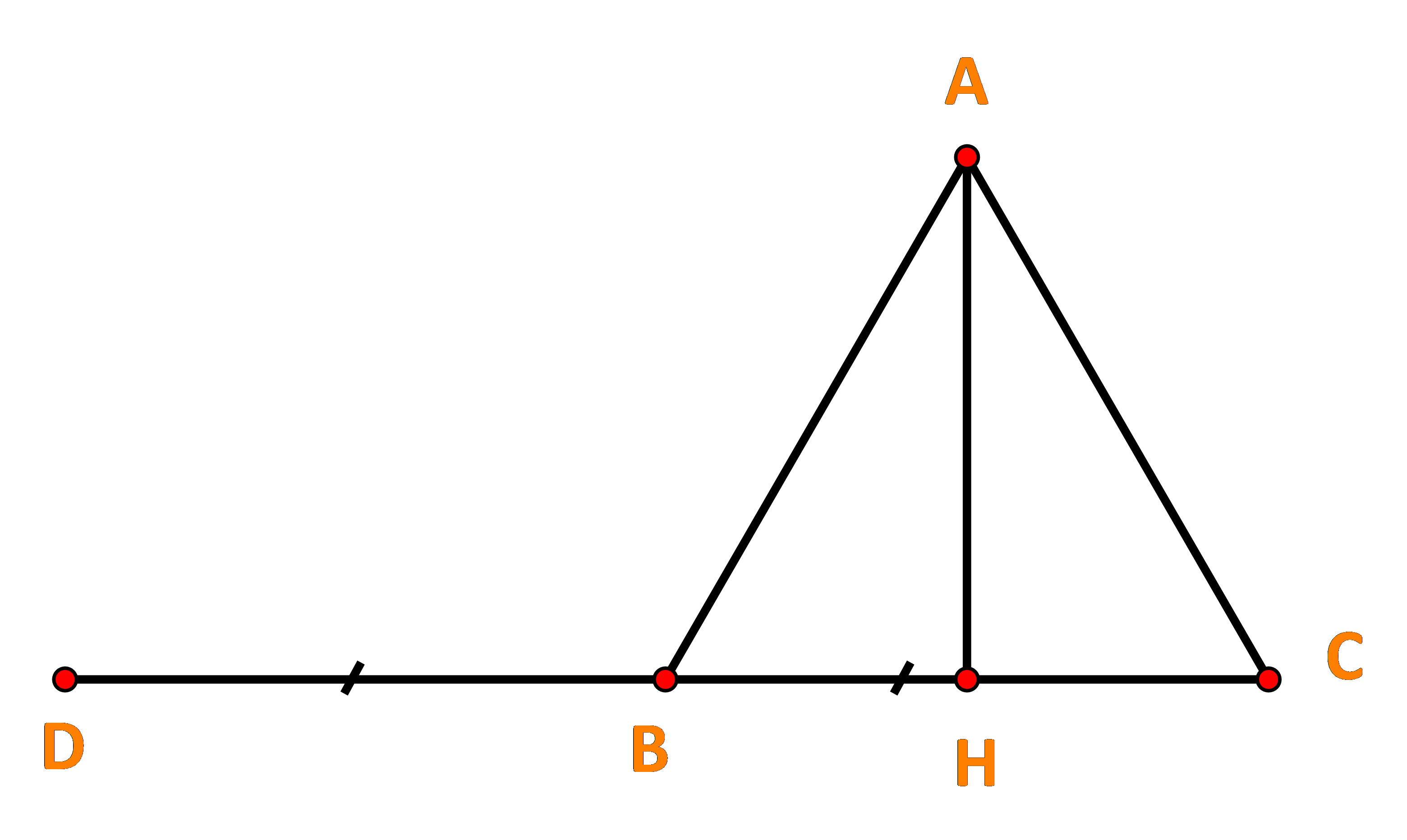
a) Vẽ vecto \(\overrightarrow {BD} = \overrightarrow {CB} \). Ta có:
\((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} ) = \widehat {DBA} = {120^o}\)
Vậy \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} ) = a.a.\cos {120^o} = {a^2}.\left( { - \frac{1}{2}} \right) = - \frac{{{a^2}}}{2}.\)
b) Vì \(AH \bot BC\) nên \[(\overrightarrow {AH} ,\overrightarrow {BC} ) = {90^o}\], suy ra \(\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = \cos {90^o} = 0.\)
Vậy \(\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = 0.\)
Cho tam giác ABC vuông tại A có \(\widehat B = {30^o},AB = 3\;cm.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} ;\;\overrightarrow {CA} .\overrightarrow {CB} .\)
Phương pháp giải:
+) Tính tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng công thức \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} )\)
Trong đó: \((\overrightarrow {BA} ,\overrightarrow {BC} ) = \widehat {ABC}\) là góc giữa hai vecto \(\overrightarrow {BA} ,\overrightarrow {BC} \)
Lời giải chi tiết:

Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)
\(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)
Cho tam giác ABC vuông tại A có \(\widehat B = {30^o},AB = 3\;cm.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} ;\;\overrightarrow {CA} .\overrightarrow {CB} .\)
Phương pháp giải:
+) Tính tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng công thức \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} )\)
Trong đó: \((\overrightarrow {BA} ,\overrightarrow {BC} ) = \widehat {ABC}\) là góc giữa hai vecto \(\overrightarrow {BA} ,\overrightarrow {BC} \)
Lời giải chi tiết:

Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)
\(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)
Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) \(\overrightarrow {CB} .\overrightarrow {BA} \)
b) \(\overrightarrow {AH} .\overrightarrow {BC} \)
Phương pháp giải:
+) Tính tích vô hướng \(\overrightarrow {CB} .\overrightarrow {BA} \) bằng công thức \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} )\)
+) \((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} )\) nếu \(\overrightarrow {BD} = \overrightarrow {CB} \)
Lời giải chi tiết:
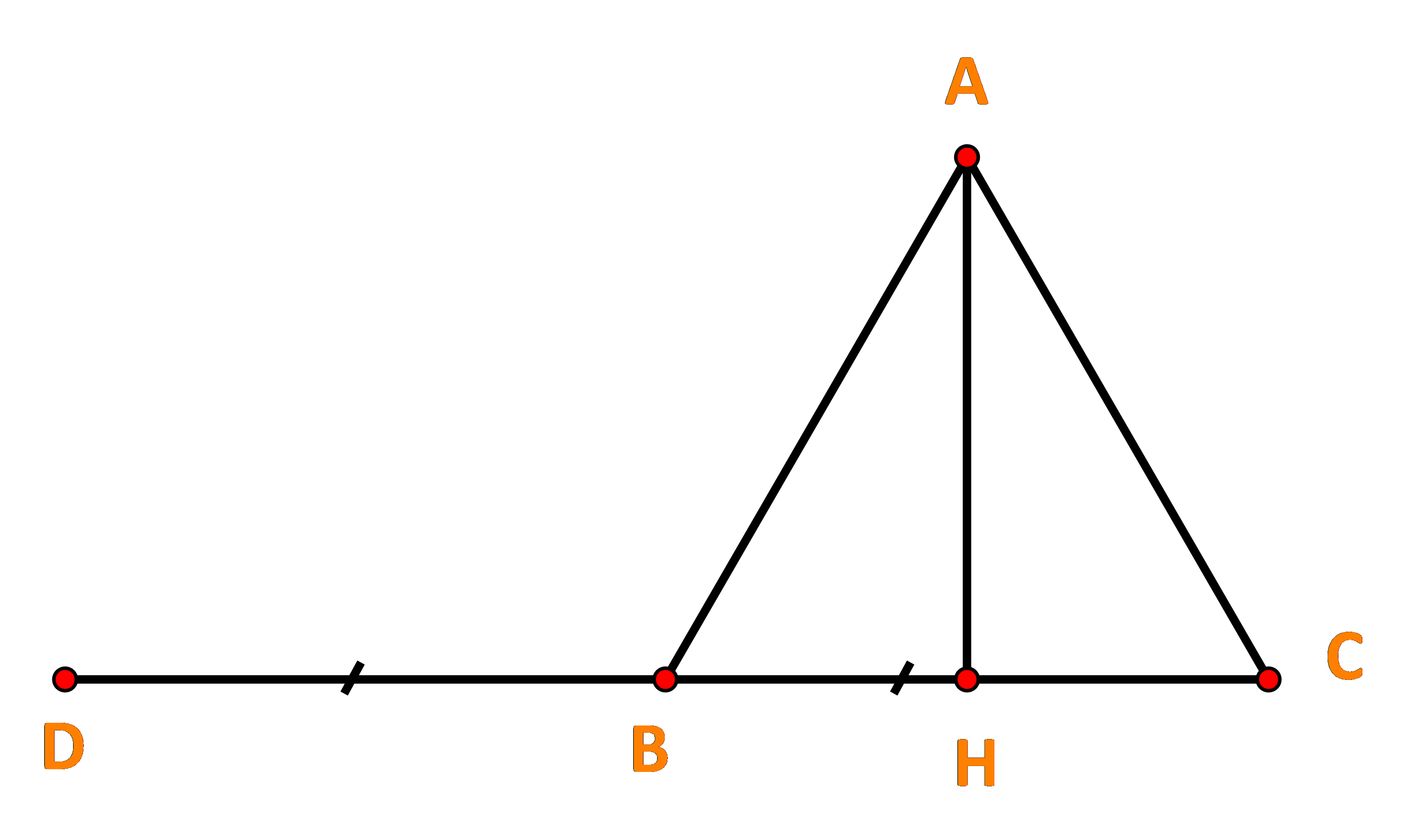
a) Vẽ vecto \(\overrightarrow {BD} = \overrightarrow {CB} \). Ta có:
\((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} ) = \widehat {DBA} = {120^o}\)
Vậy \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} ) = a.a.\cos {120^o} = {a^2}.\left( { - \frac{1}{2}} \right) = - \frac{{{a^2}}}{2}.\)
b) Vì \(AH \bot BC\) nên \[(\overrightarrow {AH} ,\overrightarrow {BC} ) = {90^o}\], suy ra \(\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = \cos {90^o} = 0.\)
Vậy \(\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = 0.\)
Mục I trong SGK Toán 10 tập 1 - Cánh diều tập trung vào việc ôn tập chương 1: Mệnh đề và tập hợp. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học về mệnh đề, tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của chúng. Việc giải các bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng tư duy logic và giải quyết vấn đề.
Bài 1 thường yêu cầu học sinh xác định tính đúng sai của các mệnh đề, xây dựng mệnh đề phủ định, và sử dụng các phép toán logic (phủ định, hội, tuyển) để kết hợp các mệnh đề. Để giải các bài tập này, học sinh cần nắm vững định nghĩa của mệnh đề, mệnh đề đúng, mệnh đề sai, và các phép toán logic.
Bài 2 thường yêu cầu học sinh thực hiện các phép toán trên tập hợp (hợp, giao, hiệu, phần bù), xác định các tập con, và chứng minh các đẳng thức tập hợp. Để giải các bài tập này, học sinh cần nắm vững định nghĩa của tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của chúng.
Bài 3 thường yêu cầu học sinh vận dụng kiến thức về mệnh đề và tập hợp để giải quyết các bài toán thực tế. Các bài toán này có thể liên quan đến việc phân loại đối tượng, tìm kiếm thông tin, hoặc đưa ra quyết định.
Ví dụ, một bài toán có thể yêu cầu học sinh phân loại các học sinh trong lớp theo giới tính và điểm trung bình. Hoặc, một bài toán có thể yêu cầu học sinh tìm kiếm các sản phẩm trong một cửa hàng thỏa mãn một số tiêu chí nhất định.
Việc giải các bài tập trong mục I trang 93, 94 SGK Toán 10 tập 1 - Cánh diều là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với hướng dẫn chi tiết và các lời khuyên trên, bạn sẽ có thể giải các bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!