Giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều một cách nhanh chóng và hiệu quả.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.

Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km.

Đề bài

Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như Hình 35. Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 148 phút.

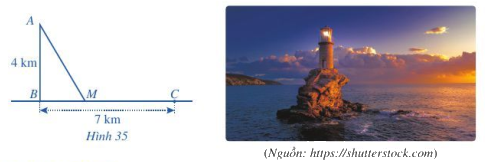
Giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều 1

Phương pháp giải - Xem chi tiết Giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều 2

- Gọi BM=x km (0<x<7)

- Biểu diễn MC, AM theo x

- Biểu diễn thời gian từ A đến M và từ M đến C theo x.

- Lập phương trình tìm x.

Lời giải chi tiết

Gọi BM=x km (0<x<7)

=> MC=7-x (km)

Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)

Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)

Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)

Tổng thời gian từ A đến C là 148 phút nên ta có:

\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)

Vậy khoảng cách từ vị trí B đến M là 3 km.

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều đặc sắc thuộc chuyên mục bài tập toán 10 trên nền tảng toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều: Tổng quan

Bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng.

Nội dung bài tập

Bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều thường bao gồm các dạng bài tập sau:

Tìm vectơ tổng, hiệu của hai vectơ: Yêu cầu học sinh thực hiện phép cộng, trừ vectơ dựa trên tọa độ hoặc biểu diễn hình học.
Tìm vectơ tích của một số với vectơ: Yêu cầu học sinh tính tích của một số thực với một vectơ, chú ý đến dấu của số thực.
Chứng minh đẳng thức vectơ: Yêu cầu học sinh sử dụng các tính chất của phép cộng, phép trừ vectơ, tích của một số với vectơ để chứng minh đẳng thức cho trước.
Ứng dụng vectơ vào giải quyết bài toán hình học: Yêu cầu học sinh sử dụng vectơ để chứng minh các tính chất của hình học, chẳng hạn như chứng minh hai đường thẳng song song, vuông góc, hoặc chứng minh một điểm nằm trên một đường thẳng.

Lời giải chi tiết bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều

Để giúp bạn hiểu rõ hơn về cách giải bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. (Lưu ý: Vì bài tập có thể thay đổi theo từng phiên bản SGK, chúng tôi sẽ cung cấp lời giải mẫu dựa trên cấu trúc chung của bài tập.)

Ví dụ 1: Tìm vectơ tổng của hai vectơ

Cho hai vectơ a = (x₁, y₁) và b = (x₂, y₂). Tìm vectơ c = a + b.

Lời giải:

c = a + b = (x₁ + x₂, y₁ + y₂)

Ví dụ 2: Tìm vectơ hiệu của hai vectơ

Cho hai vectơ a = (x₁, y₁) và b = (x₂, y₂). Tìm vectơ d = a - b.

Lời giải:

d = a - b = (x₁ - x₂, y₁ - y₂)

Ví dụ 3: Tìm vectơ tích của một số với vectơ

Cho vectơ a = (x, y) và số thực k. Tìm vectơ e = k.a.

Lời giải:

e = k.a = (k.x, k.y)

Mẹo giải bài tập vectơ hiệu quả

Nắm vững các định nghĩa và tính chất: Hiểu rõ các khái niệm về vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng là nền tảng để giải quyết các bài tập.
Sử dụng biểu diễn hình học: Vẽ hình minh họa giúp bạn hình dung rõ hơn về các vectơ và mối quan hệ giữa chúng.
Áp dụng các công thức: Sử dụng các công thức về phép cộng, phép trừ vectơ, tích của một số với vectơ một cách chính xác.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự

Để củng cố kiến thức và kỹ năng giải bài tập vectơ, bạn có thể tham khảo các bài tập tương tự sau:

Bài 6 trang 59 SGK Toán 10 tập 1 – Cánh diều
Bài 7 trang 60 SGK Toán 10 tập 1 – Cánh diều
Các bài tập trắc nghiệm về vectơ

Kết luận

Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin giải quyết bài 5 trang 59 SGK Toán 10 tập 1 – Cánh diều và các bài tập tương tự. Chúc bạn học tập tốt!