Chào mừng bạn đến với bài học về Lý thuyết Tập hợp và các phép toán trên tập hợp, một phần quan trọng trong chương trình Toán 10 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về tập hợp, các loại tập hợp, và cách thực hiện các phép toán trên chúng.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn những bài giảng dễ hiểu, bài tập đa dạng và đáp án chi tiết, giúp bạn tự tin chinh phục môn Toán.
I. TẬP HỢP II. TẬP CON VÀ TẬP HỢP BẰNG NHAU
I. TẬP HỢP
+) Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng (viết là \(\emptyset \))
+) Một tập hợp có thể không có phần tử nào, cũng có thể có một phần tử, có nhiều phần tử, có vô số phần tử
II. TẬP CON VÀ TẬP HỢP BẰNG NHAU
1. Tập con
\(A \subset B \Leftrightarrow (\forall x,x \in A \Rightarrow x \in B)\)
+) Khi \(A \subset B\), ta cũng viết \(B \supset A\)
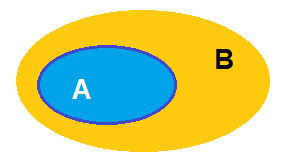
+) Nếu A không phải là tập con của B, ta viết \(A\not{ \subset }B\)
* Nhận xét:
+) \(A \subset A\;\forall A\)
+) \(A \subset B,B \subset C \Rightarrow A \subset C\)
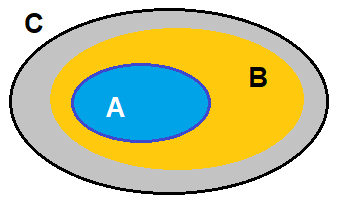
2. Tập hợp bằng nhau
\(A = B \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)
III. GIAO CỦA HAI TẬP HỢP
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
IV. HỢP CỦA HAI TẬP HỢP
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
V. PHẦN BÙ. HIỆU CỦA HAI TẬP HỢP
\(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} \) (Hiệu của A và B)
\(A \subset B\), kí hiệu: \({C_B}A = B{\rm{\backslash }}A\) (Phần bù của A trong B)
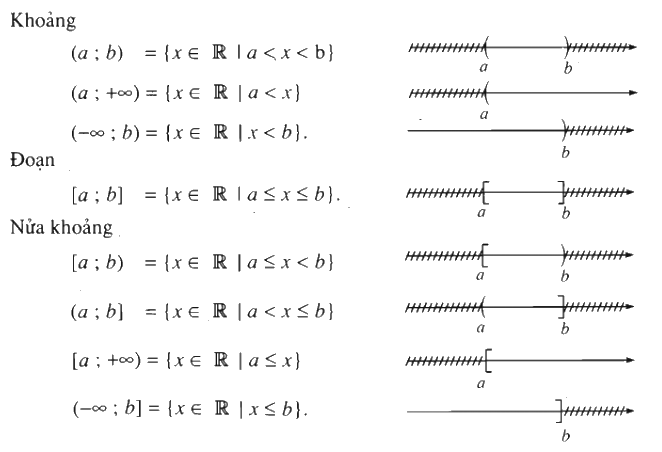
VI. CÁC TẬP HỢP SỐ
\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
Một số tập con thường dùng
Tập hợp là một khái niệm cơ bản trong toán học, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong chương trình Toán 10 Cánh diều, việc nắm vững lý thuyết tập hợp và các phép toán trên tập hợp là vô cùng quan trọng, là nền tảng cho các kiến thức toán học nâng cao hơn.
Một tập hợp là một sưu tập các đối tượng được xác định rõ ràng, gọi là các phần tử của tập hợp. Tập hợp thường được ký hiệu bằng các chữ cái in hoa như A, B, C,... và các phần tử của tập hợp được ký hiệu bằng các chữ cái in thường như a, b, c,...
Có một số loại tập hợp thường gặp trong toán học:
Có bốn phép toán cơ bản trên tập hợp:
Giả sử A = {1, 2, 3} và B = {2, 4, 5}. Ta có:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Lý thuyết tập hợp có nhiều ứng dụng trong thực tế, ví dụ như:
Để học tốt lý thuyết tập hợp, bạn nên:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Tập hợp và các phép toán trên tập hợp - SGK Toán 10 Cánh diều. Chúc bạn học tập tốt!