Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải các bài tập trong mục II trang 34, 35 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
Xét hàm số y=f(x)=x^2 Cho hàm số y=1/x và ba điểm M(-1;-1),N(0;2),P(2;1) Dựa vào Hình 4, xác định g(-2),g(0),g(2).
Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Loại các điểm không thuộc tập xác định.
- Thay hoành độ x của các điểm còn lại, kết quả ra bằng tung độ thì điểm thuộc đồ thị, ngược lại thì không.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta thấy \({x_N} = 0\)=> Điểm N không thuộc đồ thị.
Thay \({x_M} = - 1\) vào ta được: \(y = \frac{1}{{ - 1}} = - 1\)=> Điểm M thuộc đồ thị.
Thay \({x_P} = 2\) vào ta được: \(y = \frac{1}{2} \ne {y_P}\)=> Điểm P không thuộc đồ thị.
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = - 1;{x_2} = 1\).
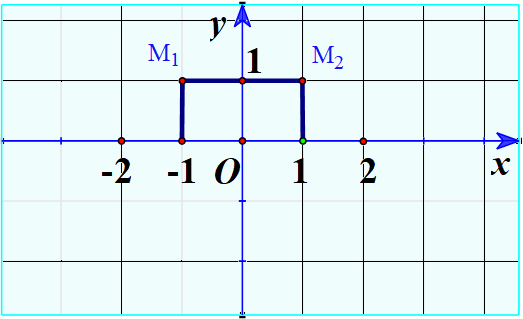
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
Phương pháp giải:
a) Thay \({x_1} = - 1;{x_2} = 1\) vào tìm \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\).
b) Xác định điểm và biểu diễn trên mặt phẳng.
Lời giải chi tiết:
a) Thay \({x_1} = - 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:
\({y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\({y_2} = f\left( 1 \right) = {1^2} = 1\)
b) Ta có \({x_1} = - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)\)
Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)
Biểu diễn trên mặt phẳng:
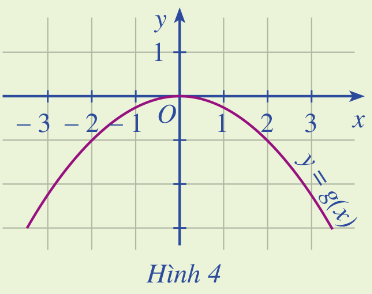
Dựa vào Hình 4, xác định \(g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)\).
Phương pháp giải:
- Xác định \(x = - 2,{\rm{ }}x = 0\) và \(x = 2\) trên trục \(Ox\).
- Kẻ đường thẳng vuông góc với \(Ox\), cắt đồ thị tại điểm nào thì lại dóng sang tung độ tìm y.
Lời giải chi tiết:
+) Với \(x = - 2\), kẻ đường thẳng vuông góc với Ox thì cắt đồ thị tại điểm có tung độ bằng \(y = - 1\)
+) Với \(x = 0 \Rightarrow y = 0\)
+) Với \(x = 2 \Rightarrow y = - 1\)
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = - 1;{x_2} = 1\).
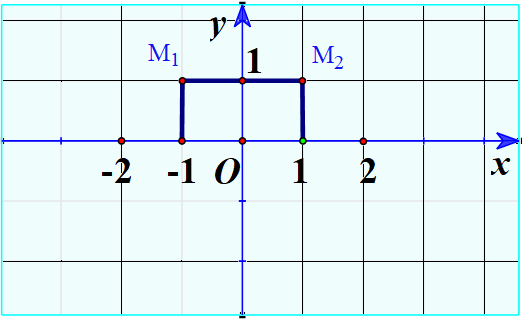
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
Phương pháp giải:
a) Thay \({x_1} = - 1;{x_2} = 1\) vào tìm \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\).
b) Xác định điểm và biểu diễn trên mặt phẳng.
Lời giải chi tiết:
a) Thay \({x_1} = - 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:
\({y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\({y_2} = f\left( 1 \right) = {1^2} = 1\)
b) Ta có \({x_1} = - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)\)
Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)
Biểu diễn trên mặt phẳng:
Cho hàm số \(y = \frac{1}{x}\) và ba điểm \(M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)\). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Loại các điểm không thuộc tập xác định.
- Thay hoành độ x của các điểm còn lại, kết quả ra bằng tung độ thì điểm thuộc đồ thị, ngược lại thì không.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta thấy \({x_N} = 0\)=> Điểm N không thuộc đồ thị.
Thay \({x_M} = - 1\) vào ta được: \(y = \frac{1}{{ - 1}} = - 1\)=> Điểm M thuộc đồ thị.
Thay \({x_P} = 2\) vào ta được: \(y = \frac{1}{2} \ne {y_P}\)=> Điểm P không thuộc đồ thị.
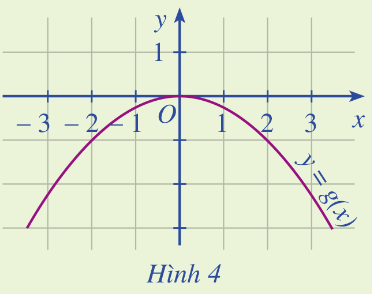
Dựa vào Hình 4, xác định \(g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)\).
Phương pháp giải:
- Xác định \(x = - 2,{\rm{ }}x = 0\) và \(x = 2\) trên trục \(Ox\).
- Kẻ đường thẳng vuông góc với \(Ox\), cắt đồ thị tại điểm nào thì lại dóng sang tung độ tìm y.
Lời giải chi tiết:
+) Với \(x = - 2\), kẻ đường thẳng vuông góc với Ox thì cắt đồ thị tại điểm có tung độ bằng \(y = - 1\)
+) Với \(x = 0 \Rightarrow y = 0\)
+) Với \(x = 2 \Rightarrow y = - 1\)
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các khái niệm và bài tập liên quan đến tập hợp số thực, các phép toán trên tập hợp số thực, và các tính chất cơ bản của chúng. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 10.
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia các số thực. Đồng thời, cần lưu ý đến thứ tự thực hiện các phép toán và các quy tắc về dấu.
Bài tập này tập trung vào việc vận dụng các tính chất giao hoán, kết hợp, phân phối của các phép toán cộng, trừ, nhân trên tập hợp số thực.
Các bài tập ứng dụng yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, ví dụ như tính diện tích hình chữ nhật, tính chu vi hình tròn, v.v.
Ví dụ: Một hình chữ nhật có chiều dài 5cm và chiều rộng 3cm. Tính diện tích của hình chữ nhật đó.
Lời giải: Diện tích hình chữ nhật được tính bằng công thức: Diện tích = Chiều dài * Chiều rộng. Vậy, diện tích của hình chữ nhật là: 5cm * 3cm = 15cm2
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính chất giao hoán của phép cộng |
| a * b = b * a | Tính chất giao hoán của phép nhân |
| a * (b + c) = a * b + a * c | Tính chất phân phối của phép nhân đối với phép cộng |
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải các bài tập trong mục II trang 34, 35 SGK Toán 10 tập 1 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!