Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
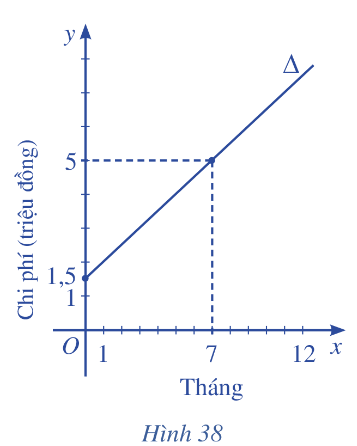
Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập.
Đề bài
Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng \(\Delta \) ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).
a) Viết phương trình của đường thẳng \(\Delta \).
b) Giao điểm của đường thẳng \(\Delta \) với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.
Phương pháp giải - Xem chi tiết
a) Phương trình đường thằng d đi qua hai điểm \(A\left( {{x_o};{y_o}} \right);B\left( {{x_1};{y_1}} \right)\) là: \(\frac{{x - {x_o}}}{{{x_1} - {x_o}}} = \frac{{y - {y_o}}}{{{y_1} - {y_o}}}\)
c) Thay giá trị tương ứng vào vào phương trình đường thẳng
Lời giải chi tiết
a) Đường thẳng \(\Delta \) đi qua hai điểm lần lượt có tọa độ \(\left( {0;1,5} \right),\left( {7;5} \right)\) nên \(\Delta \) có phương trình là:
\(\frac{{x - 0}}{{7 - 0}} = \frac{{y - 1,5}}{{5 - 1,5}} \Leftrightarrow \frac{x}{7} = \frac{{y - 1,5}}{{3,5}} \Leftrightarrow x - 2y + 3 = 0\)
b) Giao điểm của đường thẳng \(\Delta \) với trục \(Oy\) ứng với \(x = 0\). Thời điểm \(x = 0\)cho biết khoản phí tham gia ban đầu mà người tập phải trả. Khi \(x = 0\) thì \(y = 1,5\) , vì vậy khoản phí tham gia ban đầu mà người tập phải trả là 1 500 000 đồng.
c) 12 tháng đầu tiên ứng với \(x = 12\)
Từ phương trình đường thẳng \(\Delta \) ta có: \(x - 2y + 3 = 0 \Leftrightarrow y = \frac{1}{2}x + \frac{3}{2}\)
Thay \(x = 12\) vào phương trình đường thẳng ta có: \(y = \frac{1}{2}.12 + \frac{3}{2} = 7.5\)
Vậy tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục trong 12 tháng là 7tr5 nghìn đồng.
Bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 6 bao gồm các câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để giải quyết bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Cho hai vectơ a = (2; 3) và b = (-1; 4). Tính a.b.
Lời giải:
a.b = (2)(-1) + (3)(4) = -2 + 12 = 10
Cho hai vectơ a = (1; -2) và b = (3; 1). Tính cosin của góc giữa hai vectơ a và b.
Lời giải:
a.b = (1)(3) + (-2)(1) = 3 - 2 = 1
|a| = √(1² + (-2)²) = √5
|b| = √(3² + 1²) = √10
cos(θ) = (a.b) / (|a||b|) = 1 / (√5 * √10) = 1 / √50 = 1 / (5√2) = √2 / 10
Cho tam giác ABC có A(1; 2), B(3; 4), C(-1; 0). Tính góc BAC.
Lời giải:
AB = (3-1; 4-2) = (2; 2)
AC = (-1-1; 0-2) = (-2; -2)
AB.AC = (2)(-2) + (2)(-2) = -4 - 4 = -8
|AB| = √(2² + 2²) = √8 = 2√2
|AC| = √((-2)² + (-2)²) = √8 = 2√2
cos(BAC) = (AB.AC) / (|AB||AC|) = -8 / (2√2 * 2√2) = -8 / 8 = -1
=> BAC = 180°
Để củng cố kiến thức về tích vô hướng, các em có thể làm thêm các bài tập sau:
Bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ và vận dụng kiến thức về tích vô hướng của hai vectơ. Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập môn Toán.