Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài tập này thuộc chương trình học Toán 10 tập 1, tập trung vào các kiến thức về...
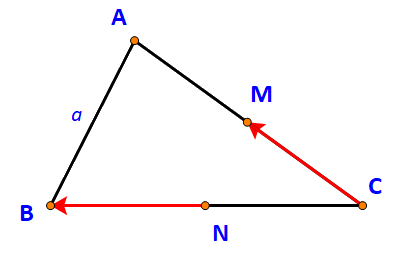
Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nahu. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
Phương pháp giải:
Bước 1: Chỉ ra \(\overrightarrow {NC} = - \overrightarrow {NB} \). Suy ra \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} \)
Bước 2: Sử dụng tính chất giao hoán, xác định vecto tổng \(\overrightarrow {CM} + \overrightarrow {NC} \)
Bước 3: Tính độ dài vecto đó theo a.
Lời giải chi tiết:
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)
\( \Rightarrow \overrightarrow {NC} = - \overrightarrow {NB} \)
Do đó: \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} = \overrightarrow {NC} + \overrightarrow {CM} \)(tính chất giáo hoán)
\( \Rightarrow \overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {NM} \Leftrightarrow \;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)
Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)
Vậy \(\;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \frac{a}{2}.\)
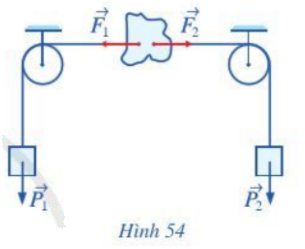
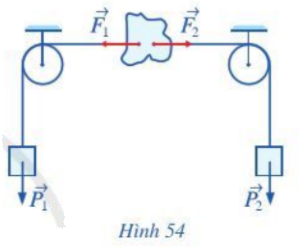
Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nahu. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Hai vật lần lượt tác động lên mảng nhựa các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} .\) Nhận xét về hướng và độ dài của mỗi cặp vecto sau:
a) \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \) biểu diễn trọng lực của hai vật
b) \(\overrightarrow {{F_1}} \) và \(\;\overrightarrow {{F_2}} .\)
(Bỏ qua trọng lượng các dây và các lực ma sát).
Phương pháp giải:
a) Nhận xét về phương, hướng và độ lớn của trọng lực của hai vật
b) Nhận xét về phương, hướng và độ lớn của hai lực.
Lời giải chi tiết:
a) Trọng lực của hai vật đều hướng xuống, vuông góc với mặt đất, đo dó chúng cùng phương, cùng hướng với nhau.
Hơn nữa: Công thức tính độ lớn trọng lực là: \(P = mg\).
Hai vật có khối lượng như nhau, do đó \({P_1} = {P_2}\)
Vậy \(\overrightarrow {{P_1}} = \overrightarrow {{P_2}} \)
b) Do trọng lực tạo thành lực kéo lên mảnh nhựa nên độ lớn của các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) là như nhau.
Chúng có hướng ngược nhau.
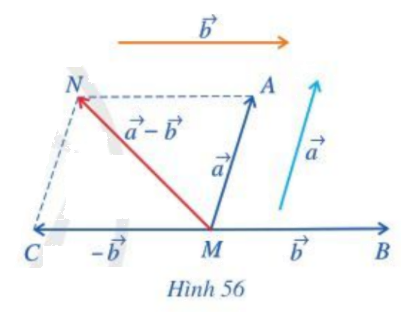
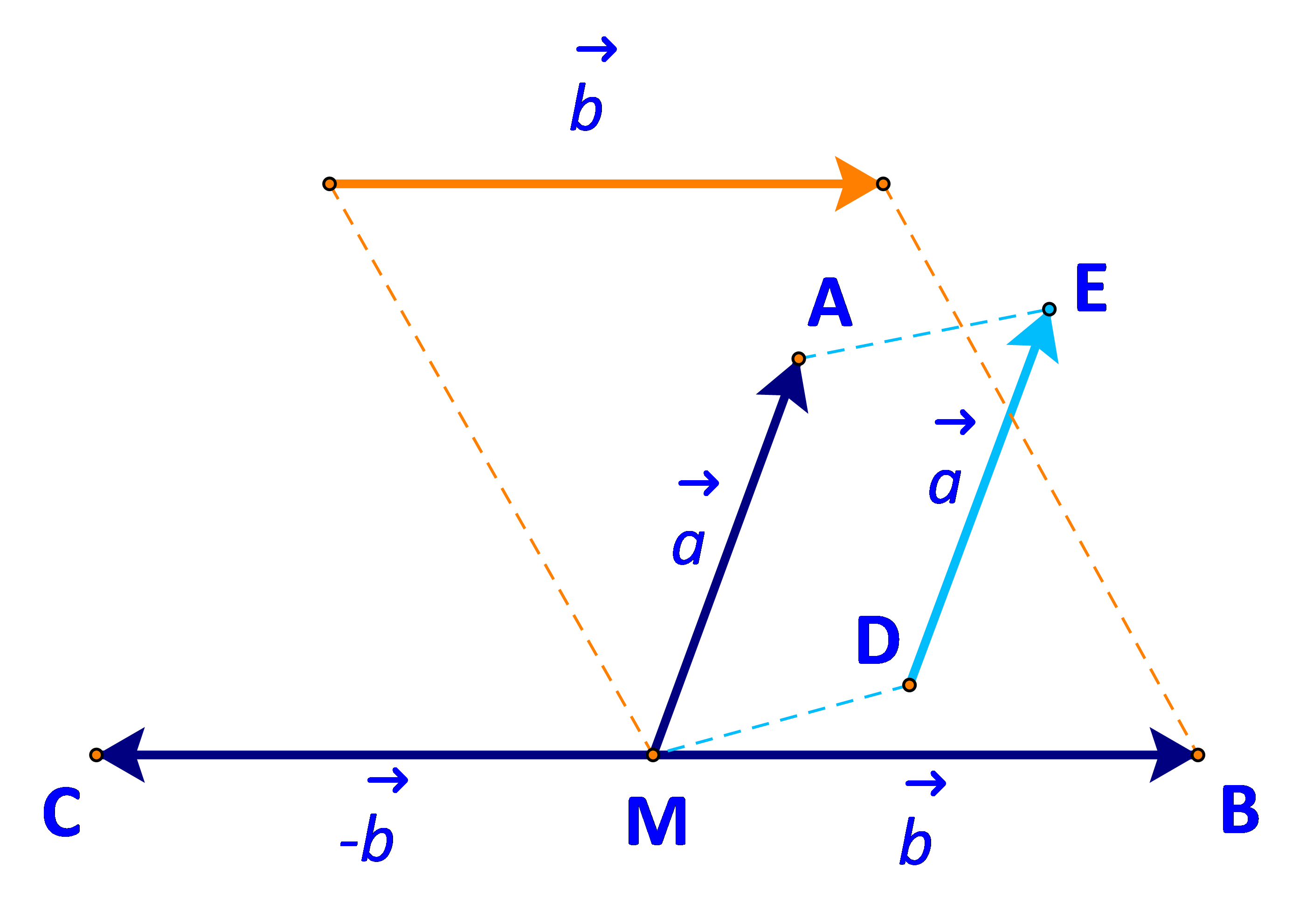
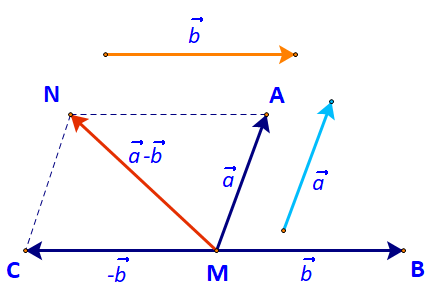
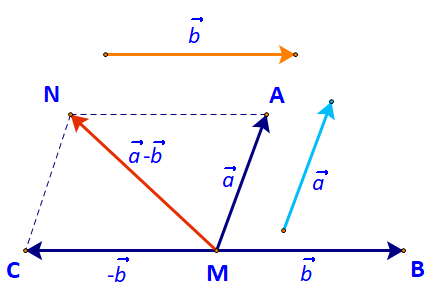
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
Phương pháp giải:
a) Áp dụng kết quả: \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \)ABCD là hình bình hành. Để xác định các điểm A, B, C.
b) Đặt vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) vào hai vecto chung gốc là hai cạnh của một hình bình hành. Từ đó xác định tổng theo quy tắc hình bình hành.
Lời giải chi tiết:
a) Đặt D, E lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Ta có: \(\overrightarrow {MA} = \overrightarrow a \)hay \(\overrightarrow {MA} = \overrightarrow {DE} \)
\( \Leftrightarrow MAED\) là hình bình hành.
Do đó A là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \)và điểm M.
Tương tự ta có:
B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \)và điểm M.
Lại có: \(\overrightarrow {MC} = - \overrightarrow b = - \overrightarrow {MB} \) do đó \(MC = MB\) và hai vecto \(\overrightarrow {MB} ,\overrightarrow {MC} \) ngược hướng nhau.
Hay M là trung điểm đoạn thẳng BC.
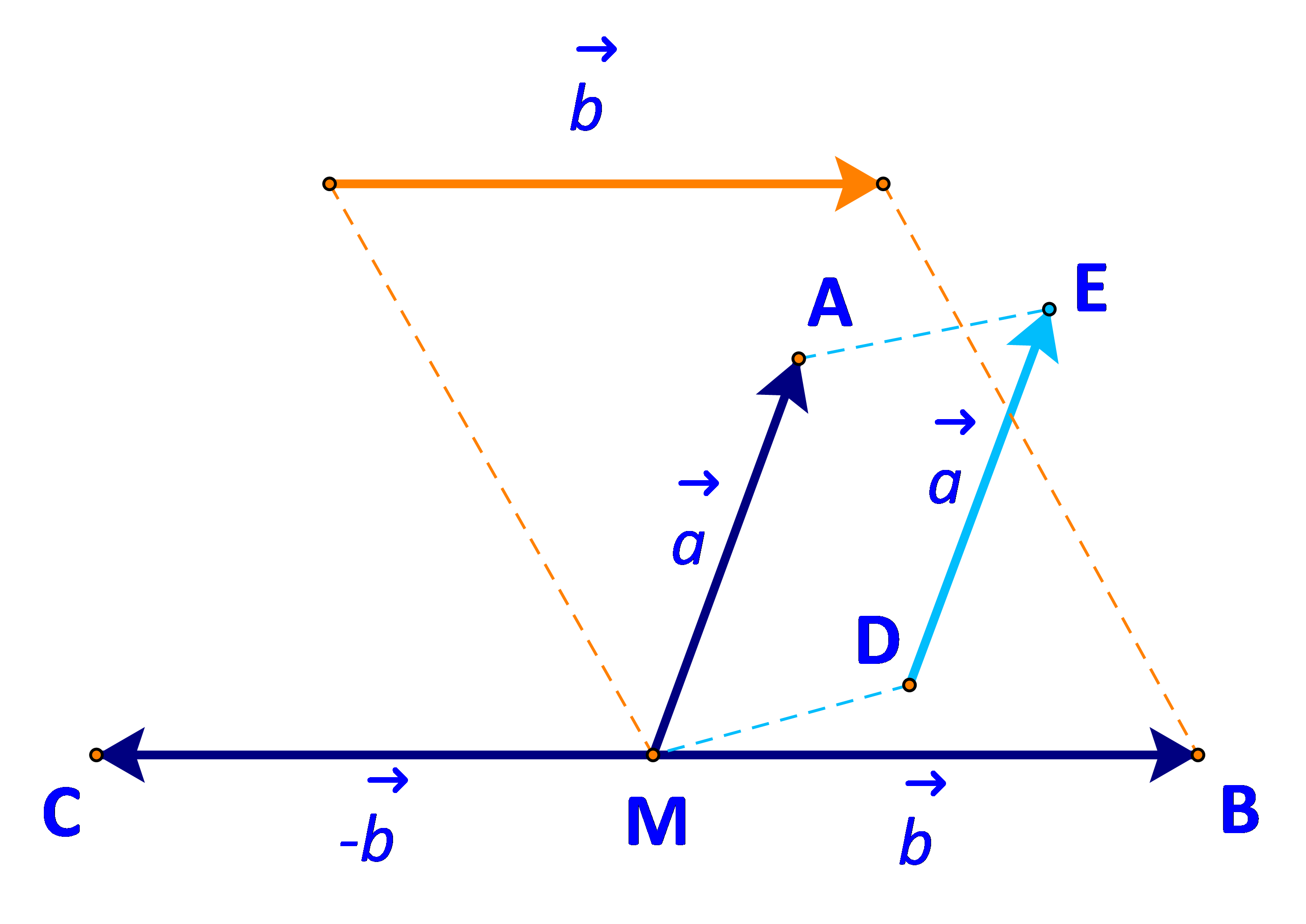
b) Lấy N là đỉnh thứ tư của hình bình hành AMCN.
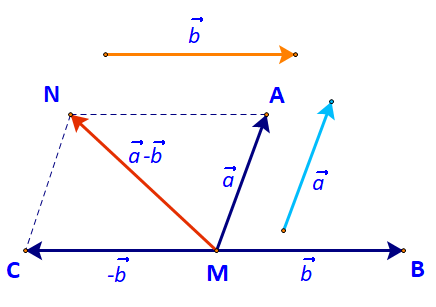
Khi đó ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \)
Mà: \(\overrightarrow {MA} = \overrightarrow a ;\;\overrightarrow {MC} = - \overrightarrow b \)
\( \Rightarrow \overrightarrow a + ( - \overrightarrow b ) = \overrightarrow {MN} \).
Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nahu. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Hai vật lần lượt tác động lên mảng nhựa các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} .\) Nhận xét về hướng và độ dài của mỗi cặp vecto sau:
a) \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \) biểu diễn trọng lực của hai vật
b) \(\overrightarrow {{F_1}} \) và \(\;\overrightarrow {{F_2}} .\)
(Bỏ qua trọng lượng các dây và các lực ma sát).
Phương pháp giải:
a) Nhận xét về phương, hướng và độ lớn của trọng lực của hai vật
b) Nhận xét về phương, hướng và độ lớn của hai lực.
Lời giải chi tiết:
a) Trọng lực của hai vật đều hướng xuống, vuông góc với mặt đất, đo dó chúng cùng phương, cùng hướng với nhau.
Hơn nữa: Công thức tính độ lớn trọng lực là: \(P = mg\).
Hai vật có khối lượng như nhau, do đó \({P_1} = {P_2}\)
Vậy \(\overrightarrow {{P_1}} = \overrightarrow {{P_2}} \)
b) Do trọng lực tạo thành lực kéo lên mảnh nhựa nên độ lớn của các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) là như nhau.
Chúng có hướng ngược nhau.
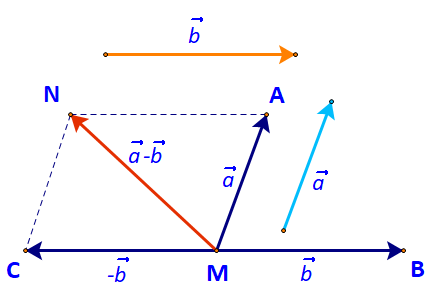
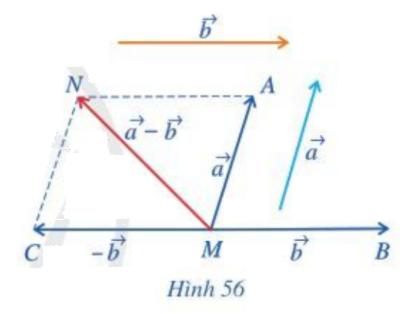
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
Phương pháp giải:
a) Áp dụng kết quả: \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \)ABCD là hình bình hành. Để xác định các điểm A, B, C.
b) Đặt vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) vào hai vecto chung gốc là hai cạnh của một hình bình hành. Từ đó xác định tổng theo quy tắc hình bình hành.
Lời giải chi tiết:
a) Đặt D, E lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Ta có: \(\overrightarrow {MA} = \overrightarrow a \)hay \(\overrightarrow {MA} = \overrightarrow {DE} \)
\( \Leftrightarrow MAED\) là hình bình hành.
Do đó A là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \)và điểm M.
Tương tự ta có:
B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \)và điểm M.
Lại có: \(\overrightarrow {MC} = - \overrightarrow b = - \overrightarrow {MB} \) do đó \(MC = MB\) và hai vecto \(\overrightarrow {MB} ,\overrightarrow {MC} \) ngược hướng nhau.
Hay M là trung điểm đoạn thẳng BC.
b) Lấy N là đỉnh thứ tư của hình bình hành AMCN.
Khi đó ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \)
Mà: \(\overrightarrow {MA} = \overrightarrow a ;\;\overrightarrow {MC} = - \overrightarrow b \)
\( \Rightarrow \overrightarrow a + ( - \overrightarrow b ) = \overrightarrow {MN} \).
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
Phương pháp giải:
Bước 1: Chỉ ra \(\overrightarrow {NC} = - \overrightarrow {NB} \). Suy ra \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} \)
Bước 2: Sử dụng tính chất giao hoán, xác định vecto tổng \(\overrightarrow {CM} + \overrightarrow {NC} \)
Bước 3: Tính độ dài vecto đó theo a.
Lời giải chi tiết:
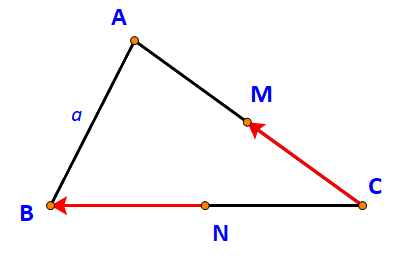
Ta có: \(\overrightarrow {NB} \) và \(\overrightarrow {NC} \) là hai vecto đối nhau (do N là trung điểm của BC)
\( \Rightarrow \overrightarrow {NC} = - \overrightarrow {NB} \)
Do đó: \(\overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {CM} + \overrightarrow {NC} = \overrightarrow {NC} + \overrightarrow {CM} \)(tính chất giáo hoán)
\( \Rightarrow \overrightarrow {CM} - \overrightarrow {NB} = \overrightarrow {NM} \Leftrightarrow \;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \;|\overrightarrow {NM} | = NM.\)
Vì: M, N lần lượt là trung điểm của AC, BC nên \(MN = \frac{1}{2}AB = \frac{a}{2}.\)
Vậy \(\;|\overrightarrow {CM} - \overrightarrow {NB} |\, = \frac{a}{2}.\)
Mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản, các định lý và phương pháp giải toán liên quan.
Mục II trang 85, 86 thường bao gồm các bài tập về:
Để giải các bài tập trong Mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:
Đề bài: ...
Lời giải: ... (Giải chi tiết bài tập 1, bao gồm các bước giải, giải thích rõ ràng)
Đề bài: ...
Lời giải: ... (Giải chi tiết bài tập 2, bao gồm các bước giải, giải thích rõ ràng)
Đề bài: ...
Lời giải: ... (Giải chi tiết bài tập 3, bao gồm các bước giải, giải thích rõ ràng)
Trong quá trình giải bài tập, học sinh cần lưu ý:
Kiến thức trong Mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Mục II trang 85, 86 SGK Toán 10 tập 1 - Cánh diều. Chúc các em học tập tốt!