Chào mừng bạn đến với bài học về Lý thuyết Tích vô hướng của hai vecto, một phần quan trọng trong chương trình Toán 10 Cánh diều. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và nâng cao về tích vô hướng, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, ứng dụng của tích vô hướng, cũng như các ví dụ minh họa cụ thể. Hãy sẵn sàng để cùng giaitoan.edu.vn chinh phục kiến thức Toán 10!
I. ĐỊNH NGHĨA II. TÍCH CHẤT III. MỘT SỐ ỨNG DỤNG
A. Lý thuyết
1. Định nghĩa
a) Tích vô hướng của hai vecto có cùng điểm đầu
Góc giữa hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) là góc giữa hai tia OA, OB và được kí hiệu là \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\). Tích vô hướng của hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) là một số thực, kí hiệu \(\overrightarrow {OA} .\overrightarrow {OB} \), được xác định bởi công thức: \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right)\). |
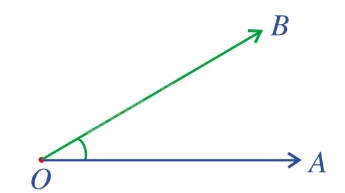
b) Tích vô hướng của hai vecto tùy ý
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\). Lấy một điểm O và vẽ vecto \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \).
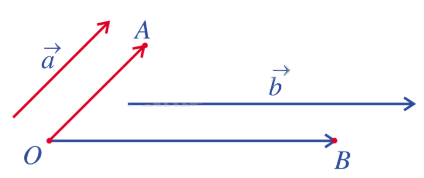
Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \), kí hiệu là \(\left( {\overrightarrow a ,\overrightarrow b } \right)\), là góc giữa hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \). Tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \), kí hiệu \(\overrightarrow a .\overrightarrow b \), là tích vô hướng của hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \). Như vậy, tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \) là một số thực được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). |
Quy ước: Tích vô hướng của một vecto bất kì vói vecto \(\overrightarrow 0 \) là số 0.
Chú ý:
+) \(\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)\).
+) Nếu \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {90^o}\) thì ta nói hai vecto \(\overrightarrow a ,\overrightarrow b \) vuông góc với nhau, kí hiệu \(\vec a \bot \vec b\) hoặc \(\overrightarrow a \bot \overrightarrow b \). Khi đó \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos {90^o} = 0\).
+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.
+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.
2. Tính chất
Với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \) và số thực k tùy ý, ta có: +) \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a \) (tính chất giao hoán). +) \(\overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c \) (tính chất phân phối). +) \(\left( {k\overrightarrow a } \right).\overrightarrow b = k\left( {\overrightarrow a .\overrightarrow b } \right) = \overrightarrow a .\left( {k\overrightarrow b } \right)\). +) \({\overrightarrow a ^2} \ge 0\), \({\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0 \). |
Trong đó, kí hiệu \(\overrightarrow a .\overrightarrow a = {\overrightarrow a ^2}\) và biểu thức này được gọi là bình phương vô hướng của vecto \(\overrightarrow a \).
3. Một số ứng dụng
a) Tính độ dài của đoạn thẳng
Nhận xét: Với hai điểm A, B phân biệt, ta có \({\overrightarrow {AB} ^2} = {\left| {\overrightarrow {AB} } \right|^2}\). Do đó, độ dài đoạn thẳng AB được tính như sau: \(AB = \sqrt {{{\overrightarrow {AB} }^2}} \).
b) Chứng minh hai đường thẳng vuông góc
Nhận xét: Cho hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \) khác \(\overrightarrow 0 \). Ta có: \(\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \overrightarrow a \bot \overrightarrow b \).
B. Bài tập
Bài 1: Cho tam giác ABC vuông cân tại A và AB = 4 cm.
a) Tính độ dài cạnh huyền BC.
b) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \); \(\overrightarrow {BA} .\overrightarrow {BC} \).
Giải:
a) \(BC = AB\sqrt 2 = 4\sqrt 2 \) (cm).
b) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
\( = 4.4.\cos \widehat {BAC} = 16.\cos {90^o} = 16.0 = 0\).
\(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\)
\( = 4.4\sqrt 2 .\cos \widehat {ABC} = 16\sqrt 2 .\cos {45^o} = 16\sqrt 2 .\frac{{\sqrt 2 }}{2} = 16\).
Bài 2: Cho hình vuông ABCD tâm O có độ dài cạnh bằng a. Tính:
a) \(\overrightarrow {AB} .\overrightarrow {OC} \).
b) \(\overrightarrow {AB} .\overrightarrow {BD} \).
c) \(\overrightarrow {AB} .\overrightarrow {OD} \).
Giải:
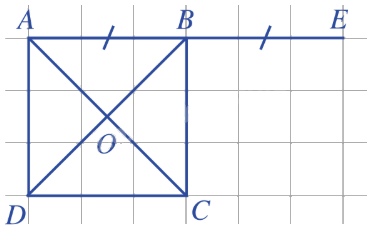
a) Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {OC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \widehat {BAO} = {45^o}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {OC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {OC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {OC} } \right) = a.\frac{a}{{\sqrt 2 }}.\cos {45^o} = \frac{{{a^2}}}{{\sqrt 2 }}.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}}}{2}\).
b) Vẽ vecto \(\overrightarrow {BE} = \overrightarrow {AB} \). Ta có:
\(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BD} } \right) = \widehat {EBD} = {135^o}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {BD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = a.a\sqrt 2 .\cos {135^o} = {a^2}\sqrt 2 .\frac{{ - \sqrt 2 }}{2} = - {a^2}\).
c) Vì \(\overrightarrow {BE} = \overrightarrow {AB} \), \(\overrightarrow {BO} = \overrightarrow {OD} \) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {OD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BO} } \right) = \widehat {EBO} = {135^o}\).
Vậy \(\overrightarrow {AB} .\overrightarrow {OD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {OD} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {OD} } \right) = a.\frac{a}{{\sqrt 2 }}.\cos {135^o} = \frac{{{a^2}}}{{\sqrt 2 }}.\frac{{ - \sqrt 2 }}{2} = \frac{{ - {a^2}}}{2}\).
Bài 3: Cho đoạn thẳng AB và I là trung điểm của AB. Chứng minh rằng với mỗi điểm O, ta có:
a) \(\overrightarrow {OI} .\overrightarrow {IA} + \overrightarrow {OI} .\overrightarrow {IB} = 0\).
b) \(\overrightarrow {OI} .\overrightarrow {AB} = \frac{1}{2}\left( {{{\overrightarrow {OB} }^2} - {{\overrightarrow {OA} }^2}} \right)\).
Giải:
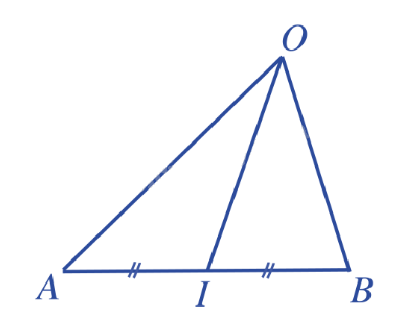
a) Vì I là trung điểm của AB nên \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).
Vậy \(\overrightarrow {OI} .\overrightarrow {IA} + \overrightarrow {OI} .\overrightarrow {IB} = \overrightarrow {OI} .\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = \overrightarrow {OI} .\overrightarrow 0 = 0\).
b) Vì I là trung điểm AB nên \(2\overrightarrow {OI} = \overrightarrow {OB} + \overrightarrow {OA} \Leftrightarrow \overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OA} } \right)\).
Vậy \(\overrightarrow {OI} .\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OA} } \right).\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) = \frac{1}{2}.\left( {{{\overrightarrow {OB} }^2} - {{\overrightarrow {OA} }^2}} \right)\).
Bài 4: Cho tam giác ABC vuông tại A. Tính \(\overrightarrow {AB} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {BC} \).
Giải:
\(\overrightarrow {AB} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {AB} .\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) = \overrightarrow {AB} .\overrightarrow {AC} = 0\) (do \(\overrightarrow {AB} \) vuông góc với \(\overrightarrow {AC} \)).
Bài 5: Chứng minh rằng trong tam giác ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\) (định lí cosin trong tam giác).
Giải:
Ta có \({\overrightarrow {BC} ^2} = {\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)^2} = {\overrightarrow {AC} ^2} + {\overrightarrow {AB} ^2} - 2.\overrightarrow {AC} .\overrightarrow {AB} \).
Suy ra \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
\( = A{B^2} + A{C^2} - 2AB.AC.\cos A\).
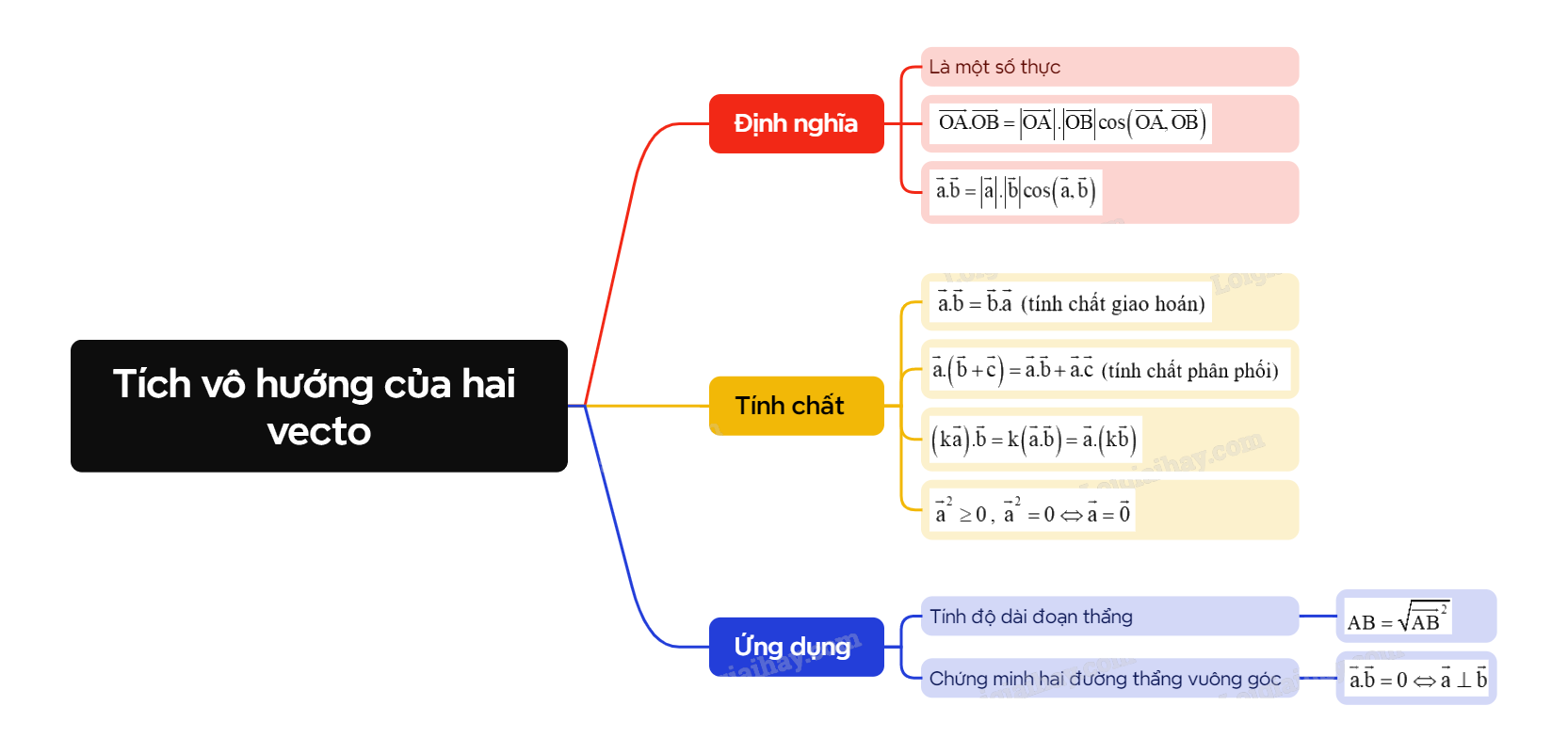
Tích vô hướng của hai vecto là một khái niệm quan trọng trong hình học giải tích lớp 10, đặc biệt trong chương trình Toán 10 Cánh diều. Nó cho phép chúng ta tính toán góc giữa hai vecto và xác định mối quan hệ vuông góc giữa chúng.
Cho hai vecto a = (a1; a2) và b = (b1; b2). Tích vô hướng của a và b, ký hiệu là a.b, được định nghĩa là:
a.b = a1b1 + a2b2
Nếu a và b là hai vecto khác 0, thì góc θ giữa hai vecto được tính bởi công thức:
cos θ = a.b / (||a|| . ||b||)
Bài 1: Cho a = (2; -1) và b = (1; 3). Tính a.b.
Giải:a.b = 2*1 + (-1)*3 = 2 - 3 = -1
Bài 2: Cho a = (1; 0) và b = (0; 1). Tính góc θ giữa hai vecto.
Giải: cos θ = (a.b) / (||a|| . ||b||) = (1*0 + 0*1) / (√(12 + 02) . √(02 + 12)) = 0 / (1*1) = 0. Suy ra θ = 90o.
Lý thuyết tích vô hướng của hai vecto là một công cụ mạnh mẽ trong hình học giải tích, giúp chúng ta giải quyết nhiều bài toán liên quan đến góc, khoảng cách và mối quan hệ giữa các vecto. Việc nắm vững kiến thức này là rất quan trọng để học tốt môn Toán 10 và các môn học liên quan sau này.