Chào mừng bạn đến với bài học về lý thuyết Phương trình đường tròn, một phần quan trọng trong chương trình Toán 10 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và cần thiết để hiểu rõ về phương trình đường tròn, cách xác định tâm và bán kính của đường tròn từ phương trình, và ứng dụng của phương trình đường tròn trong giải toán.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và nhiều bài tập thực hành để bạn có thể tự tin chinh phục môn Toán.
A. Lý thuyết 1. Phương trình đường tròn a) Phương trình đường tròn Điểm M(x;y) nằm trên đường tròn (C) khi và chỉ khi
A. Lý thuyết
1. Phương trình đường tròn
a) Phương trình đường tròn
Điểm M(x;y) nằm trên đường tròn (C) khi và chỉ khi
\(IM = R \Leftrightarrow I{M^2} = {R^2} \Leftrightarrow {(x - a)^2} + {(y - b)^2} = {R^2}\).
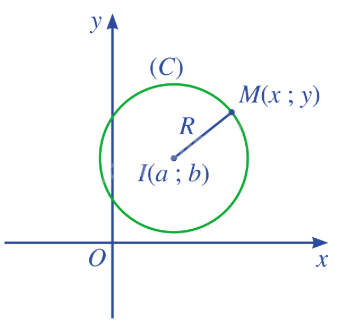
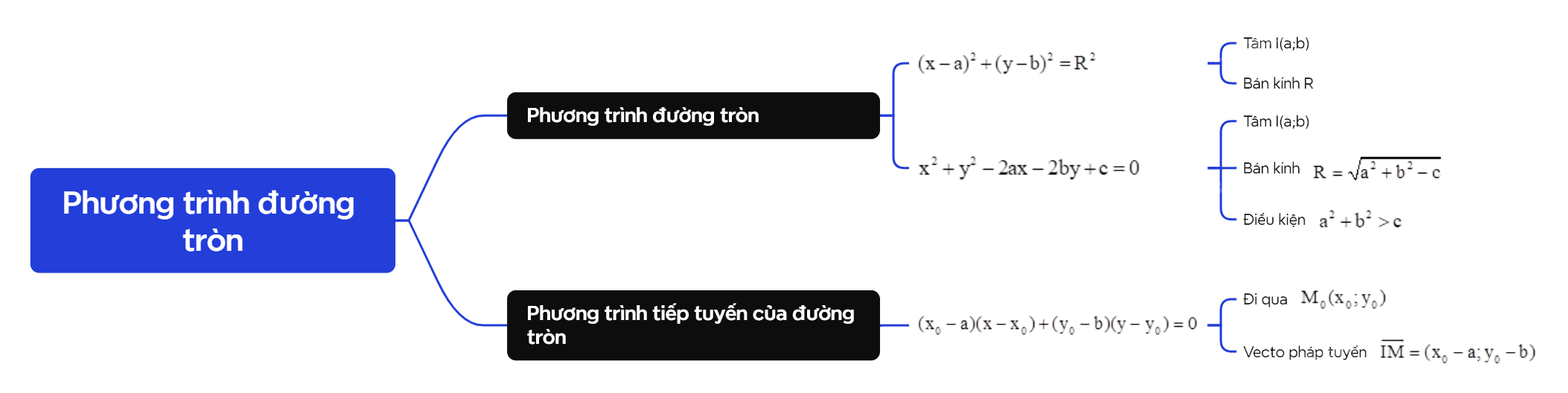
Phương trình đường tròn tâm I(a;b) bán kính R là \({(x - a)^2} + {(y - b)^2} = {R^2}\). |
Phương trình đường tròn có thể viết ở dạng \({(x - a)^2} + {(y - b)^2} = {R^2}\) (chính tắc) hoặc đưa về dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) (tổng quát).
Nhận xét: Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của một đường tròn (C) khi và chỉ khi \({a^2} + {b^2} > c\). Khi đó, (C) có tâm I(a;b) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} \).
b) Phương trình đường tròn đi qua ba điểm không thẳng hàng
Do có duy nhất một đường tròn đi qua ba điểm không thẳng hàng cho trước nên ta có thể lập được phương trình đường tròn đó khi biết tọa độ của ba điểm nói trên.
2. Phương trình tiếp tuyến của đường tròn
Cho đường tròn (C) tâm I(a;b) và điểm \({M_0}({x_0};{y_0})\) nằm trên đường tròn đó. Gọi \(\Delta \) là tiếp tuyến của (C) tại điểm \({M_0}({x_0};{y_0})\). Khi đó:
Đường thẳng \(\Delta \) đi qua điểm \({M_0}({x_0};{y_0})\) và có vecto pháp tuyến \(\overrightarrow {IM} = ({x_0} - a;{y_0} - b)\). Phương trình tiếp tuyến \(\Delta \) là \(({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0\). |
B. Bài tập
Bài 1:
a) Tìm tâm và bán kính đường tròn (C) có phương trình: \({(x - 2)^2} + {(y + 3)^2} = 16\).
b) Viết phương trình đường tròn (C’) tâm J(2;-1) và có bán kính gấp đôi bán kính đường tròn (C).
Giải:
a) Ta viết phương trình của (C) ở dạng \({(x - 2)^2} + {(y - ( - 3))^2} = {4^2}\).
Vậy (C) có tâm I(2;-3) và bán kính R = 4.
b) Đường tròn (C’) có tâm J(2;-1) và bán kính R’ = 2R = 8 nên có phương trình:
\({(x - 2)^2} + {(y + 1)^2} = 64\).
Bài 2: Phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) có phải là phương trình đường tròn không? Nếu có, xác định tọa độ tâm và bán kính của đường tròn đó.
Giải:
Từ phương trình, ta có \(a = \frac{{ - 4}}{{ - 2}} = 2\); \(b = \frac{2}{{ - 2}} = - 1\); c = -4.
Suy ra \({a^2} + {b^2} - c = {2^2} + {( - 1)^2} - ( - 4) = 9 > 0\).
Vậy phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) là phương trình đường tròn tâm I(2;-1) và bán kính \(R = \sqrt 9 = 3\).
Bài 3: Lập phương trình đường tròn đi qua ba điểm A(-1;1), B(0;-2), C(0;2).
Giải:
Giả sử tâm của đường tròn là điểm I(a;b). Ta có \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\).
Khi đó:
\(\left\{ \begin{array}{l}{( - 1 - a)^2} + {(1 - b)^2} = {(0 - a)^2} + {( - 2 - b)^2}\\{(0 - a)^2} + {( - 2 - b)^2} = {(0 - a)^2} + {(2 - b)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a - 2b + 2 = {a^2} + {b^2} + 4b + 4\\{a^2} + {b^2} + 4b + 4 = {a^2} + {b^2} - 4b + 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2a - 2b = 4b + 2\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\).
Đường tròn tâm I(1;0) bán kính \(R = IC = \sqrt {{a^2} + {b^2} - 4b + 4} = \sqrt 5 \).
Phương trình đường tròn là \({(x - 1)^2} + {(y - 0)^2} = {(\sqrt 5 )^2}\).
Vậy phương trình đường tròn là \({(x - 1)^2} + {y^2} = 5\).
Bài 4: Cho đường tròn (C) có phương trình \({(x + 1)^2} + {(y - 3)^2} = 5\). Điểm M(0;1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).
Giải:
Do \({(0 + 1)^2} + {(1 - 3)^2} = 5\), nên điểm M thuộc (C).
Đường tròn (C) có tâm là I(-1;3). Tiếp tuyến của (C) tại M(0;1) có vecto pháp tuyến \( - 1(x - 0) + 2(y - 1) = 0 \Leftrightarrow x - 2y + 2 = 0\).
Phương trình đường tròn là một khái niệm quan trọng trong hình học giải tích, giúp mô tả quỹ tích của các điểm cách một điểm cố định (tâm) một khoảng không đổi (bán kính). Bài viết này sẽ trình bày chi tiết lý thuyết về phương trình đường tròn theo chương trình SGK Toán 10 Cánh diều, bao gồm định nghĩa, các dạng phương trình, cách xác định tâm và bán kính, và các ứng dụng cơ bản.
Trong mặt phẳng tọa độ Oxy, đường tròn (C) có tâm I(a; b) và bán kính R được định nghĩa là tập hợp tất cả các điểm M(x; y) sao cho khoảng cách từ M đến I bằng R. Khoảng cách này được tính theo công thức: IM = √((x - a)² + (y - b)²).
Phương trình đường tròn (C) có tâm I(a; b) và bán kính R được viết như sau:
(x - a)² + (y - b)² = R²
Từ dạng tổng quát, ta có thể xác định tâm và bán kính của đường tròn bằng các công thức:
Phương trình x² + y² - 2ax - 2by + c = 0 là phương trình của một đường tròn khi và chỉ khi:
a² + b² - c > 0
Nếu a² + b² - c = 0, phương trình biểu diễn một điểm (tâm đường tròn).
Nếu a² + b² - c < 0, phương trình không biểu diễn tập hợp điểm nào.
Ví dụ 1: Xác định tâm và bán kính của đường tròn có phương trình: x² + y² - 4x + 6y - 3 = 0
Ta có: a = 2, b = -3, c = -3
a² + b² - c = 2² + (-3)² - (-3) = 4 + 9 + 3 = 16 > 0
Vậy, đây là phương trình của một đường tròn có:
Ví dụ 2: Viết phương trình đường tròn có tâm I(-1; 2) và bán kính R = 3
Áp dụng dạng chính tắc, ta có phương trình:
(x - (-1))² + (y - 2)² = 3²
(x + 1)² + (y - 2)² = 9
Phương trình đường tròn có nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học, ví dụ:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và cần thiết về lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và tự tin giải các bài toán liên quan.