Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục III trang 36 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) So sánh f(-2),f(-1). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1. b) So sánh f(1), f(2). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Cho hàm số \(f\left( x \right) = x + 1\).
a) So sánh \(f\left( 1 \right)\) và \(f\left( 2 \right)\).
b) Chứng minh rằng nếu \({x_1},{x_2} \in \mathbb{R}\) sao cho \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Phương pháp giải:
a) Tính \(f\left( 1 \right)\) và \(f\left( 2 \right)\) và so sánh .
b) Thay \({x_1},{x_2}\) vào \(f\left( x \right) = x + 1\) tìm \(f\left( {{x_1}} \right),f\left( {{x_2}} \right)\) rồi chứng minh \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Lời giải chi tiết:
a) Ta có:
\(f\left( 1 \right) = 1 + 1 = 2\)
\(f\left( 2 \right) = 2 + 1 = 3\)
\( \Rightarrow f\left( 2 \right) > f\left( 1 \right)\)
b) Ta có:
\(f\left( {{x_1}} \right) = {x_1} + 1;f\left( {{x_2}} \right) = {x_2} + 1\)
\(\begin{array}{l}f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {{x_1} + 1} \right) - \left( {{x_2} + 1} \right)\\ = {x_1} - {x_2} < 0\end{array}\)
Vậy \({x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Phương pháp giải:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Lời giải chi tiết:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Ta có: \(f\left( {{x_1}} \right) = 6x_1^2;f\left( {{x_2}} \right) = 6x_2^2\)
\(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 6x_1^2 - 6x_2^2\)\( = 6\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right)\)
\({x_1} < {x_2} \Rightarrow {x_1} - {x_2} < 0\)
\({x_1} < 0;{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\)
Vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
Cho đồ thị hàm số \(y = f\left( x \right) = {x^2}\) như Hình 6.
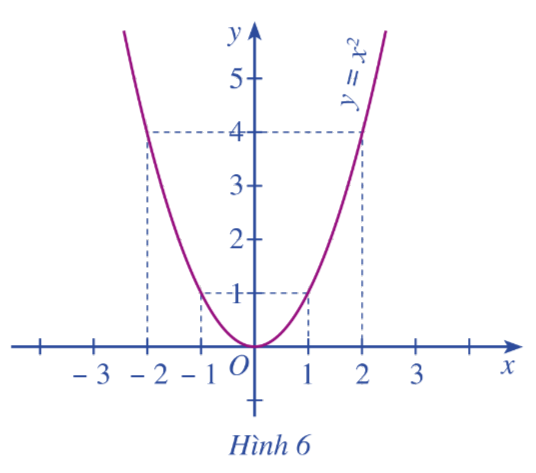
a) So sánh \(f\left( { - 2} \right),f\left( { - 1} \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.
b) So sánh \(f\left( 1 \right),f\left( 2 \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Phương pháp giải:
a)
- Tính \(f\left( { - 2} \right),f\left( { - 1} \right)\)
- Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
b)
- Tính \(f\left( 1 \right),f\left( 2 \right)\)
- Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.
Cho hàm số \(f\left( x \right) = x + 1\).
a) So sánh \(f\left( 1 \right)\) và \(f\left( 2 \right)\).
b) Chứng minh rằng nếu \({x_1},{x_2} \in \mathbb{R}\) sao cho \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Phương pháp giải:
a) Tính \(f\left( 1 \right)\) và \(f\left( 2 \right)\) và so sánh .
b) Thay \({x_1},{x_2}\) vào \(f\left( x \right) = x + 1\) tìm \(f\left( {{x_1}} \right),f\left( {{x_2}} \right)\) rồi chứng minh \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Lời giải chi tiết:
a) Ta có:
\(f\left( 1 \right) = 1 + 1 = 2\)
\(f\left( 2 \right) = 2 + 1 = 3\)
\( \Rightarrow f\left( 2 \right) > f\left( 1 \right)\)
b) Ta có:
\(f\left( {{x_1}} \right) = {x_1} + 1;f\left( {{x_2}} \right) = {x_2} + 1\)
\(\begin{array}{l}f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {{x_1} + 1} \right) - \left( {{x_2} + 1} \right)\\ = {x_1} - {x_2} < 0\end{array}\)
Vậy \({x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Phương pháp giải:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Lời giải chi tiết:
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Ta có: \(f\left( {{x_1}} \right) = 6x_1^2;f\left( {{x_2}} \right) = 6x_2^2\)
\(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 6x_1^2 - 6x_2^2\)\( = 6\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right)\)
\({x_1} < {x_2} \Rightarrow {x_1} - {x_2} < 0\)
\({x_1} < 0;{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\)
Vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
Cho đồ thị hàm số \(y = f\left( x \right) = {x^2}\) như Hình 6.
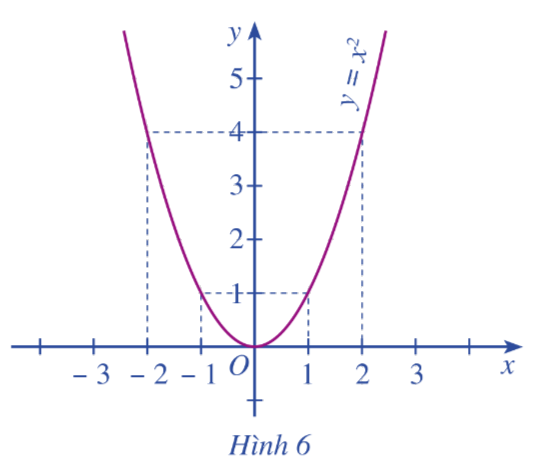
a) So sánh \(f\left( { - 2} \right),f\left( { - 1} \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khi giá trị biến x tăng dần từ -2 đến -1.
b) So sánh \(f\left( 1 \right),f\left( 2 \right)\). Nêu nhận xét về sự biến thiên của giá trị hàm số khị giá trị biến x tăng dần từ 1 đến 2.
Phương pháp giải:
a)
- Tính \(f\left( { - 2} \right),f\left( { - 1} \right)\)
- Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
b)
- Tính \(f\left( 1 \right),f\left( 2 \right)\)
- Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\). Chứng minh \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết:
a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.
Mục III trang 36 SGK Toán 10 tập 1 - Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học phẳng. Các bài tập trong mục này thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh tìm tọa độ của các vectơ được tạo bởi các điểm cho trước. Để giải bài này, học sinh cần nắm vững công thức tính tọa độ của vectơ:
Cho hai điểm A(xA; yA) và B(xB; yB). Khi đó, vectơ AB có tọa độ là (xB - xA; yB - yA).
Ví dụ: Cho A(1; 2) và B(3; 4). Khi đó, vectơ AB có tọa độ là (3 - 1; 4 - 2) = (2; 2).
Bài 2 yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân với một số trên các vectơ cho trước. Để giải bài này, học sinh cần nắm vững các quy tắc sau:
Bài 3 yêu cầu học sinh chứng minh các đẳng thức vectơ. Để giải bài này, học sinh cần sử dụng các quy tắc biến đổi vectơ và các tính chất của phép toán vectơ.
Ví dụ: Để chứng minh đẳng thức AB = CD, ta có thể chứng minh AB2 = CD2 bằng cách sử dụng công thức tính độ dài của vectơ.
Bài 4 yêu cầu học sinh sử dụng vectơ để giải quyết các bài toán liên quan đến hình học phẳng. Để giải bài này, học sinh cần kết hợp kiến thức về vectơ với kiến thức về hình học phẳng (tính chất đường thẳng, tam giác, hình bình hành,...).
Ví dụ: Để chứng minh ba điểm A, B, C thẳng hàng, ta có thể chứng minh vectơ AB và vectơ AC cùng phương.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ:
Hy vọng rằng, với những hướng dẫn chi tiết trên, bạn đã có thể tự tin giải quyết các bài tập trong mục III trang 36 SGK Toán 10 tập 1 - Cánh diều. Chúc bạn học tập tốt!