Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 10 Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
Phương pháp giải:
a) Quan sát hình 6, dựa vào các góc đồng vị và tam giác cân để suy ra \(\widehat {xON} = {180^o} - \alpha \)
b) Trên hình vẽ, xác định các GTLG của \(\widehat {xON}\),so sánh với GTLG của góc \(\alpha \).
Lời giải chi tiết:
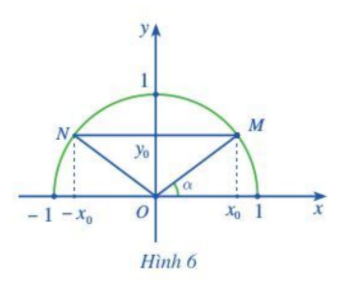
a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Phương pháp giải:
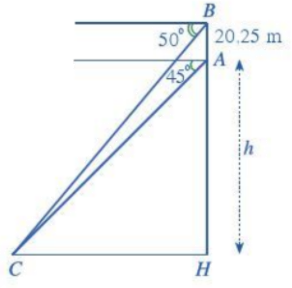
Bước 1: Tính \(\widehat {ACH},\widehat {BCH}\)
Bước 2: Tính \(\tan \widehat {ACH},\tan \widehat {BCH}\) theo h.
Bước 3: Giải phương trình ẩn h và kết luận.
Lời giải chi tiết:
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và \(\widehat {xOM} = \alpha \).
a) Chứng minh \(\widehat {xON} = {180^o} - \alpha \)
b) Biểu diễn giá trị lượng giác của góc \({180^o} - \alpha \) theo giá trị lượng giác của góc \(\alpha \).
Phương pháp giải:
a) Quan sát hình 6, dựa vào các góc đồng vị và tam giác cân để suy ra \(\widehat {xON} = {180^o} - \alpha \)
b) Trên hình vẽ, xác định các GTLG của \(\widehat {xON}\),so sánh với GTLG của góc \(\alpha \).
Lời giải chi tiết:
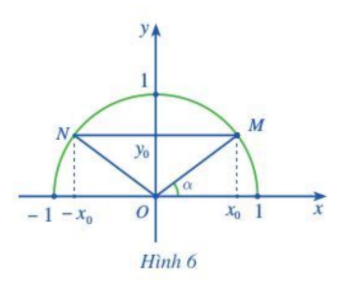
a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Phương pháp giải:
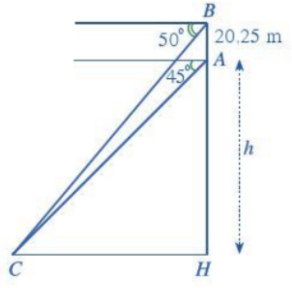
Bước 1: Tính \(\widehat {ACH},\widehat {BCH}\)
Bước 2: Tính \(\tan \widehat {ACH},\tan \widehat {BCH}\) theo h.
Bước 3: Giải phương trình ẩn h và kết luận.
Lời giải chi tiết:
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.
Mục I trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức nâng cao hơn trong chương trình Toán học.
Trang 63 tập trung vào việc xác định các loại tập hợp số (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số vô tỉ, tập số thực) và thực hiện các phép toán cơ bản trên chúng như hợp, giao, hiệu, phần bù. Các bài tập thường yêu cầu học sinh phân loại các số cho trước vào các tập hợp tương ứng, hoặc tìm các tập hợp thỏa mãn các điều kiện nhất định.
Trang 64 giới thiệu khái niệm về khoảng và đoạn trên trục số, bao gồm các loại khoảng (khoảng mở, khoảng đóng, nửa mở nửa đóng). Học sinh cần nắm vững cách biểu diễn các khoảng và đoạn trên trục số, và thực hiện các phép toán trên chúng. Các bài tập thường yêu cầu học sinh xác định các khoảng và đoạn thỏa mãn các điều kiện nhất định, hoặc tìm các số thuộc hoặc không thuộc một khoảng hoặc đoạn cho trước.
Trang 65 tập trung vào khái niệm về tập hợp con, và các tính chất của tập hợp con. Học sinh cần nắm vững cách xác định một tập hợp là tập hợp con của một tập hợp khác, và thực hiện các phép toán trên tập hợp con. Các bài tập thường yêu cầu học sinh xác định các tập hợp con của một tập hợp cho trước, hoặc chứng minh một tập hợp là tập hợp con của một tập hợp khác.
Trang 66 là phần tổng hợp các kiến thức đã học về tập hợp, bao gồm các phép toán trên tập hợp, khoảng và đoạn trên trục số, và tập hợp con. Các bài tập thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán phức tạp hơn.
Bài tập: Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Tìm A ∪ B và A ∩ B.
Giải:
Để học tốt môn Toán, các em cần thường xuyên luyện tập, làm bài tập, và tìm hiểu các phương pháp giải bài tập hiệu quả. Hãy sử dụng giaitoan.edu.vn như một công cụ hỗ trợ đắc lực trong quá trình học tập của mình.
| Công thức | Mô tả |
|---|---|
| A ∪ B | Hợp của A và B |
| A ∩ B | Giao của A và B |
| A \ B | Hiệu của A và B |