Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục II trang 83, 84 SGK Toán 10 tập 2 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục II trang 83, 84 tập trung vào các kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học.
Quan sát Hình 40a và đọc tên một góc nhọn trong bốn góc đó. a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng Trong mặt phẳng toạ độ, cho hai đường thẳng Tính số đo góc giữa hai đường thẳng
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)\). Tính \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\).
Lời giải chi tiết:
Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\)
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\)
Lời giải chi tiết:
a) \({\Delta _1}\) có vecto chỉ phương là \(\overrightarrow {{u_1}} = \left( {3\sqrt 3 ;3} \right)\), từ đó ta suy ra vecto pháp tuyến là \(\overrightarrow {{n_1}} = \left( { - 3;3\sqrt 3 } \right)\).
Các vecto pháp tuyến của \({\Delta _1}\), \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( { - 3;3\sqrt 3 } \right)\) và \(\overrightarrow {{n_2}} = (0;1)\).
\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| { - 3.0 + 3\sqrt 3 .1} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {{\left( {3\sqrt 3 } \right)}^2}} .\sqrt {{0^2} + {1^2}} }} = \frac{{\sqrt 3 }}{2}\), suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\).
b) Các vecto pháp tuyến của \({\Delta _1}\), \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\) và \(\overrightarrow {{n_2}} = ( - 1;3)\).
\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {2.( - 1) - 1.3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}\), suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\).
Trong mặt phẳng, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau tại A tạo thành bốn góc đỉnh A (quy ước không kể góc bẹt và góc không).
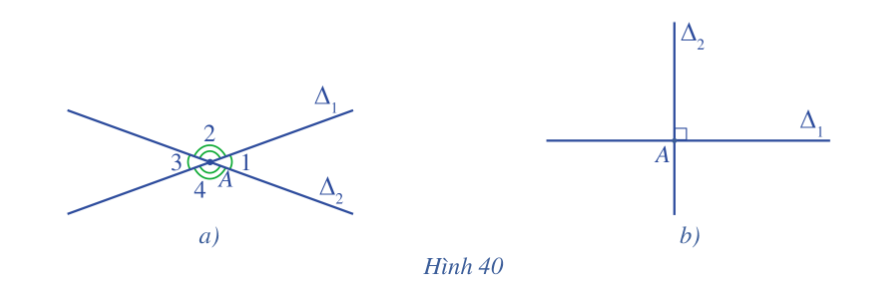
Quan sát Hình 40a và đọc tên một góc nhọn trong bốn góc đó.
Quan sát Hình 40b và nêu đặc điểm bốn góc tại đỉnh A.
Lời giải chi tiết:
Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.
Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.
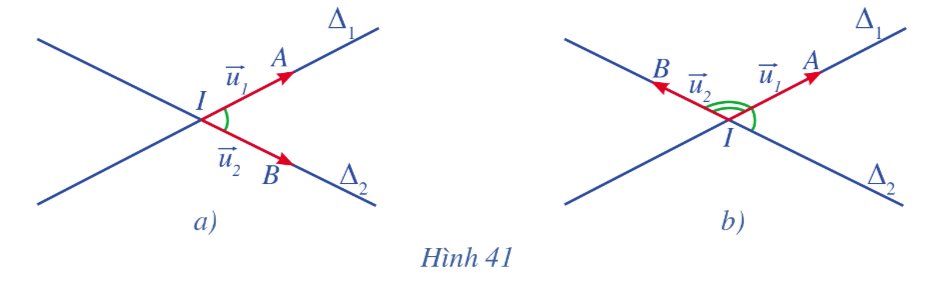
Cho hai đường thẳng \({\Delta _1},{\Delta _2}\) cắt nhau tại I và có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng \({\Delta _1}\), \({\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \), \(\overrightarrow {IB} \).
b) Chứng tỏ \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,\overrightarrow {IB} } \right)} \right|\).
Lời giải chi tiết:
a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1}\), \({\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \), \(\overrightarrow {IB} \) có thể bẳng nhau hoặc bù nhau.
b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\) thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).
Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).
Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
Trong mặt phẳng, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau tại A tạo thành bốn góc đỉnh A (quy ước không kể góc bẹt và góc không).
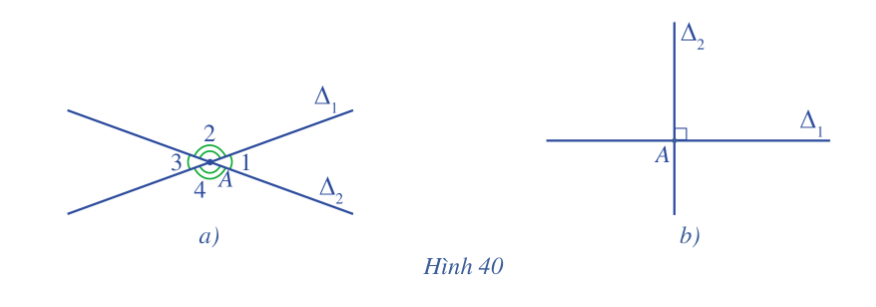
Quan sát Hình 40a và đọc tên một góc nhọn trong bốn góc đó.
Quan sát Hình 40b và nêu đặc điểm bốn góc tại đỉnh A.
Lời giải chi tiết:
Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.
Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.
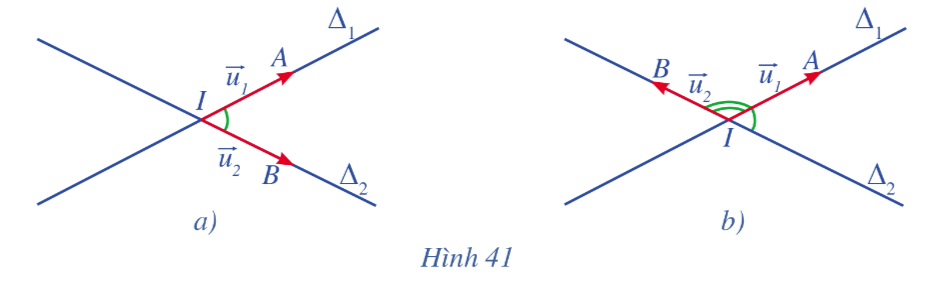
Cho hai đường thẳng \({\Delta _1},{\Delta _2}\) cắt nhau tại I và có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng \({\Delta _1}\), \({\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \), \(\overrightarrow {IB} \).
b) Chứng tỏ \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,\overrightarrow {IB} } \right)} \right|\).
Lời giải chi tiết:
a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1}\), \({\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \), \(\overrightarrow {IB} \) có thể bẳng nhau hoặc bù nhau.
b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\) thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).
Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).
Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} = {\rm{ }}\left( {{a_1};{\rm{ }}{b_1}} \right),{\rm{ }}\overrightarrow {{u_2}} {\rm{ }} = {\rm{ }}\left( {{a_2};{b_2}} \right)\). Tính \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\).
Lời giải chi tiết:
Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 3 + 3\sqrt 3 t\\y = 2 + 3t\end{array} \right.\) và \({\Delta _2}:y - 4 = 0\)
b) \({\Delta _1}:2x - y = 0\) và \({\Delta _2}: - x + 3y - 5 = 0\)
Lời giải chi tiết:
a) \({\Delta _1}\) có vecto chỉ phương là \(\overrightarrow {{u_1}} = \left( {3\sqrt 3 ;3} \right)\), từ đó ta suy ra vecto pháp tuyến là \(\overrightarrow {{n_1}} = \left( { - 3;3\sqrt 3 } \right)\).
Các vecto pháp tuyến của \({\Delta _1}\), \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( { - 3;3\sqrt 3 } \right)\) và \(\overrightarrow {{n_2}} = (0;1)\).
\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| { - 3.0 + 3\sqrt 3 .1} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {{\left( {3\sqrt 3 } \right)}^2}} .\sqrt {{0^2} + {1^2}} }} = \frac{{\sqrt 3 }}{2}\), suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\).
b) Các vecto pháp tuyến của \({\Delta _1}\), \({\Delta _2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\) và \(\overrightarrow {{n_2}} = ( - 1;3)\).
\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {2.( - 1) - 1.3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}\), suy ra \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\).
Mục II trang 83, 84 SGK Toán 10 tập 2 - Cánh diều là một phần quan trọng trong chương trình học vectơ của học sinh lớp 10. Nội dung chính của mục này xoay quanh việc vận dụng các kiến thức đã học về vectơ để giải quyết các bài toán liên quan đến hình học phẳng. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các tính chất của chúng.
Mục II bao gồm một loạt các bài tập với độ khó tăng dần, từ việc xác định các vectơ, thực hiện các phép toán vectơ đơn giản đến việc chứng minh các đẳng thức vectơ và giải các bài toán hình học phức tạp hơn. Dưới đây là phân tích chi tiết một số bài tập tiêu biểu:
Bài tập này yêu cầu học sinh xác định các vectơ trong hình vẽ, thực hiện các phép cộng, trừ vectơ và biểu diễn kết quả bằng vectơ mới. Để giải bài tập này, học sinh cần hiểu rõ quy tắc cộng, trừ vectơ (quy tắc hình bình hành, quy tắc tam giác) và cách biểu diễn vectơ bằng tọa độ.
Bài tập này yêu cầu học sinh nhân một vectơ với một số thực và xác định vectơ kết quả. Học sinh cần nhớ rằng khi nhân một vectơ với một số thực, độ dài của vectơ mới sẽ bằng độ dài của vectơ ban đầu nhân với giá trị tuyệt đối của số thực, và hướng của vectơ mới sẽ cùng hướng với vectơ ban đầu nếu số thực dương và ngược hướng nếu số thực âm.
Đây là loại bài tập đòi hỏi học sinh phải vận dụng các tính chất của phép cộng, trừ vectơ, phép nhân vectơ với một số thực và các quy tắc hình học để chứng minh một đẳng thức vectơ nào đó. Để giải bài tập này, học sinh cần phân tích kỹ đề bài, tìm ra mối liên hệ giữa các vectơ và sử dụng các công cụ toán học phù hợp để chứng minh đẳng thức.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải quyết các bài toán hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, tính diện tích hình bình hành, hình tam giác,... Để giải bài tập này, học sinh cần kết hợp kiến thức về vectơ với kiến thức về hình học phẳng.
Để học tốt môn Toán nói chung và phần vectơ nói riêng, học sinh cần dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Ngoài ra, việc sử dụng các tài liệu tham khảo, các trang web học toán online như giaitoan.edu.vn cũng là một cách hiệu quả để nâng cao kiến thức và kỹ năng giải bài tập.
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán 10.