Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 15, 16, 17 sách giáo khoa Toán 10 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho tập hợp A = {a, b, c, d, e}. Trong một buổi tập huấn cho các bí thư chi đoàn có 10 bạn nam. Dùng máy tính cầm tay để tính:
Trong một buổi tập huấn cho các bí thư chi đoàn có 10 bạn nam. Hỏi có bao nhiều cách chọn 3 bạn nam để tham gia một trò chơi?
Lời giải chi tiết:
Mỗi cách chọn 3 bạn nam trong 10 bạn nam là một tổ hợp chập 3 của 10 phần tử.
Do đó có \(C_{10}^3 = 120\) (cách chọn)
Dùng máy tính cầm tay để tính:
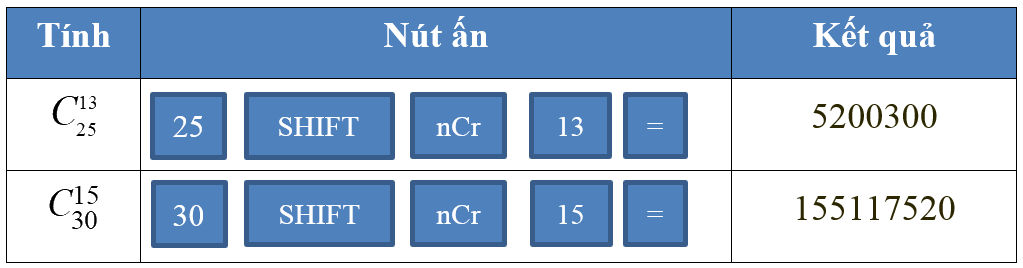
a)\(C_{25}^{13}\)
b)\(C_{30}^{25}\)
Lời giải chi tiết:
Cho tập hợp A = {a, b, c, d, e}.
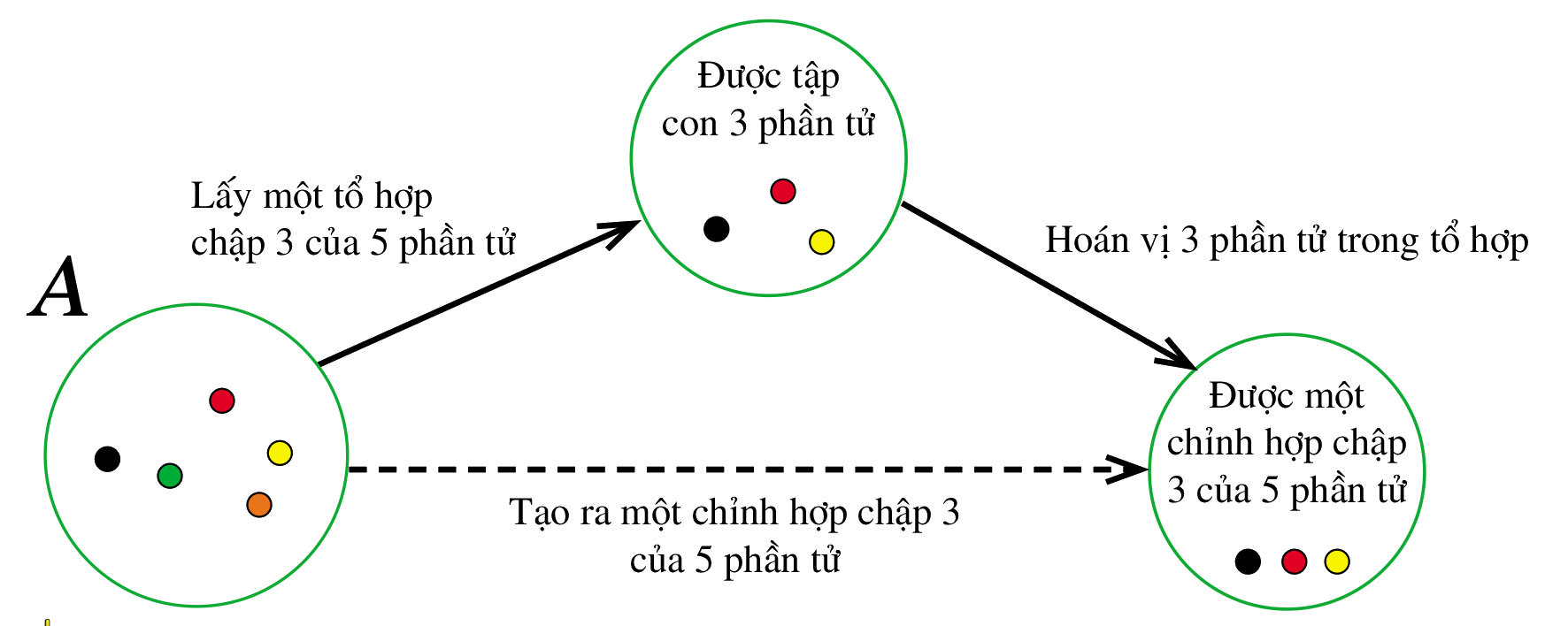
a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.
c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
Lời giải chi tiết:
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh:Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
Cho tập hợp A = {a, b, c, d, e}.
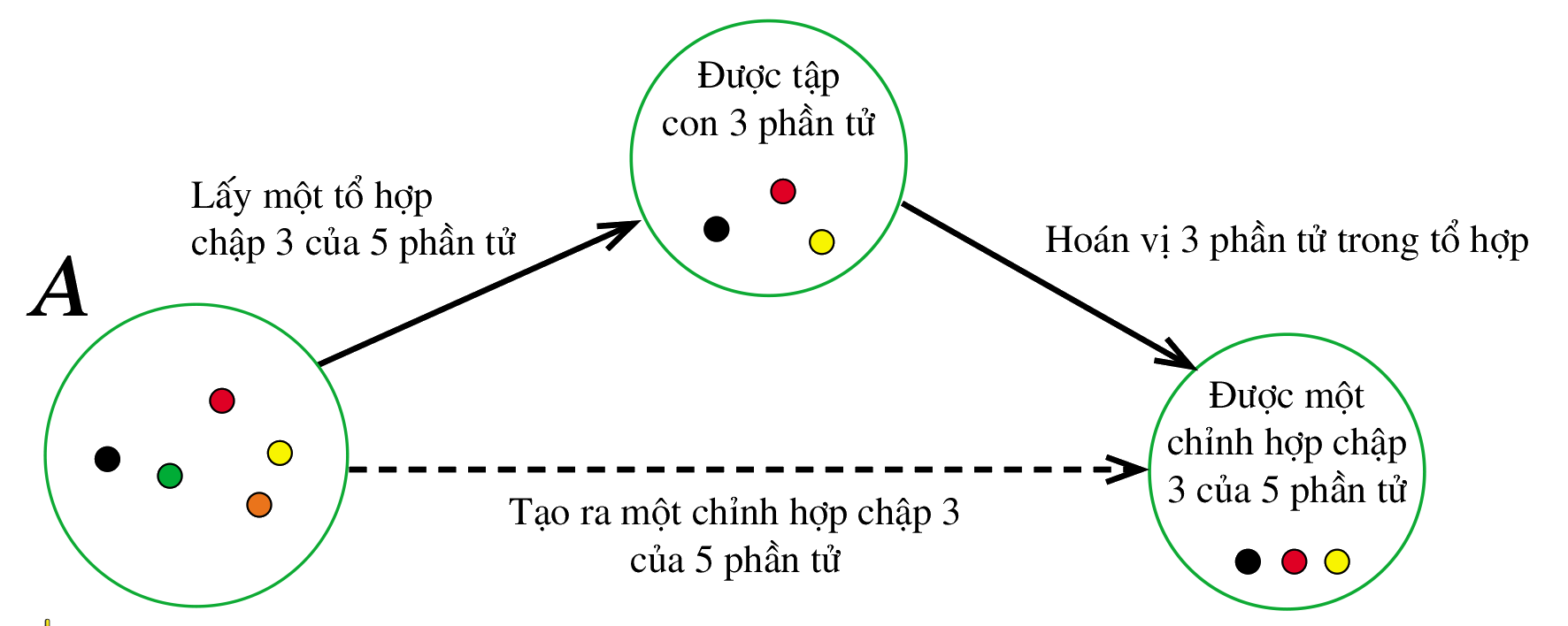
a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.
c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
Lời giải chi tiết:
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh:Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
Trong một buổi tập huấn cho các bí thư chi đoàn có 10 bạn nam. Hỏi có bao nhiều cách chọn 3 bạn nam để tham gia một trò chơi?
Lời giải chi tiết:
Mỗi cách chọn 3 bạn nam trong 10 bạn nam là một tổ hợp chập 3 của 10 phần tử.
Do đó có \(C_{10}^3 = 120\) (cách chọn)
Dùng máy tính cầm tay để tính:
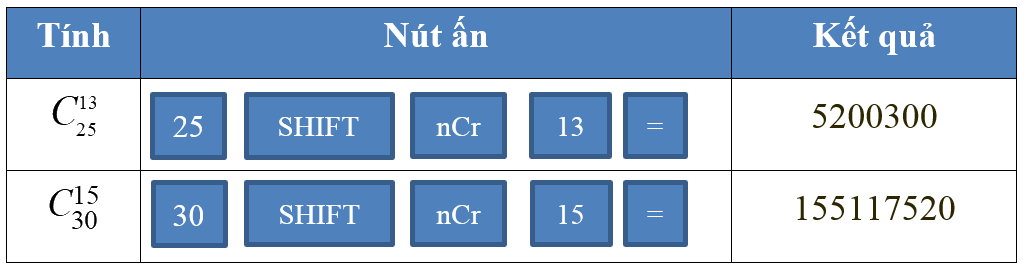
a)\(C_{25}^{13}\)
b)\(C_{30}^{25}\)
Lời giải chi tiết:
Mục II trong SGK Toán 10 tập 2 - Cánh diều tập trung vào các kiến thức về vectơ, đặc biệt là các phép toán trên vectơ và ứng dụng của vectơ trong hình học. Việc nắm vững các khái niệm và kỹ năng trong mục này là nền tảng quan trọng cho việc học tập các kiến thức toán học ở các lớp trên.
Bài tập này yêu cầu học sinh thực hiện các phép cộng và trừ vectơ dựa trên các quy tắc đã học. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của phép cộng và phép trừ vectơ, cũng như các tính chất của các phép toán này.
Bài tập này yêu cầu học sinh thực hiện phép nhân một vectơ với một số thực. Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của phép nhân vectơ với một số thực, cũng như các tính chất của phép toán này.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải các bài toán hình học. Để giải bài tập này, học sinh cần hiểu rõ mối liên hệ giữa vectơ và các yếu tố hình học như điểm, đường thẳng, đoạn thẳng.
Ví dụ: Cho tam giác ABC. Tìm vectơ AB và AC. Tính độ dài của cạnh BC.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| (a + b) + c = a + (b + c) | Tính kết hợp của phép cộng vectơ |
| k(a + b) = ka + kb | Tính chất phân phối của phép nhân với phép cộng vectơ |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục II trang 15, 16, 17 SGK Toán 10 tập 2 - Cánh diều. Chúc các em học tập tốt!