Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục II trang 73, 74, 75 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho tam giác ABC có AB = 12; B = 60; C = 45. Tính diện tích của tam giác ABC. Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Phương pháp giải:
Bước 1: Tính AC, bằng cách áp dụng định lí sin trong tam giác ABC.
Bước 2: Tính \(\widehat A\). Suy ra diện tích tam giác ABC bằng công thức \(S = \frac{1}{2}bc.\sin A\)
Lời giải chi tiết:
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
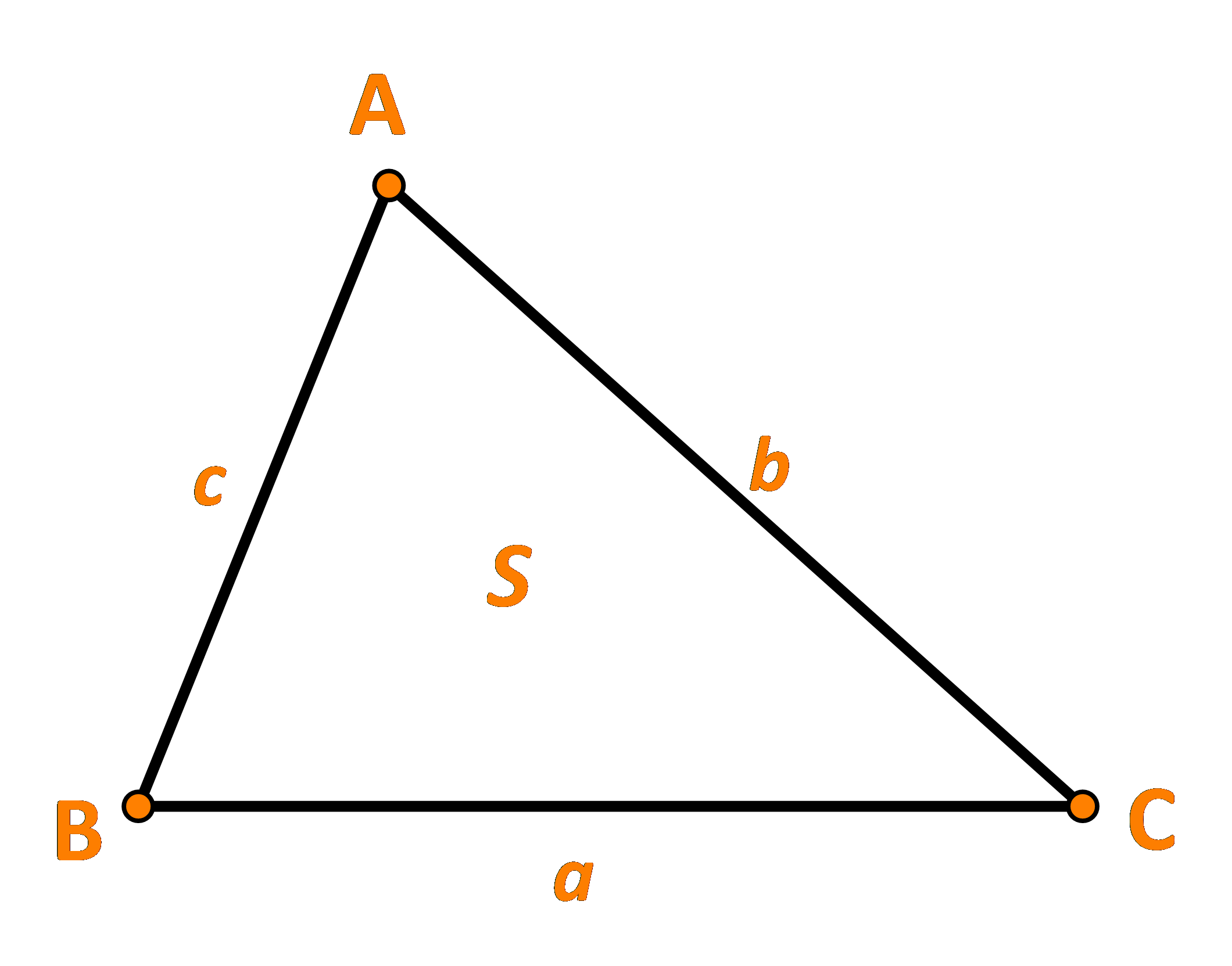
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
a) Từ định lí cosin, chứng tỏ rằng:
\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)
b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Phương pháp giải:
Bước 1: Tính cos A theo a, b, c.
Bước 2: Tính sin A theo cos A.
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)
\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)
Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)
b) Ta có: \(S = \frac{1}{2}bc\sin A\)
Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)
\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Phương pháp giải:
Bước 1: Tính AC, bằng cách áp dụng định lí sin trong tam giác ABC.
Bước 2: Tính \(\widehat A\). Suy ra diện tích tam giác ABC bằng công thức \(S = \frac{1}{2}bc.\sin A\)
Lời giải chi tiết:
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
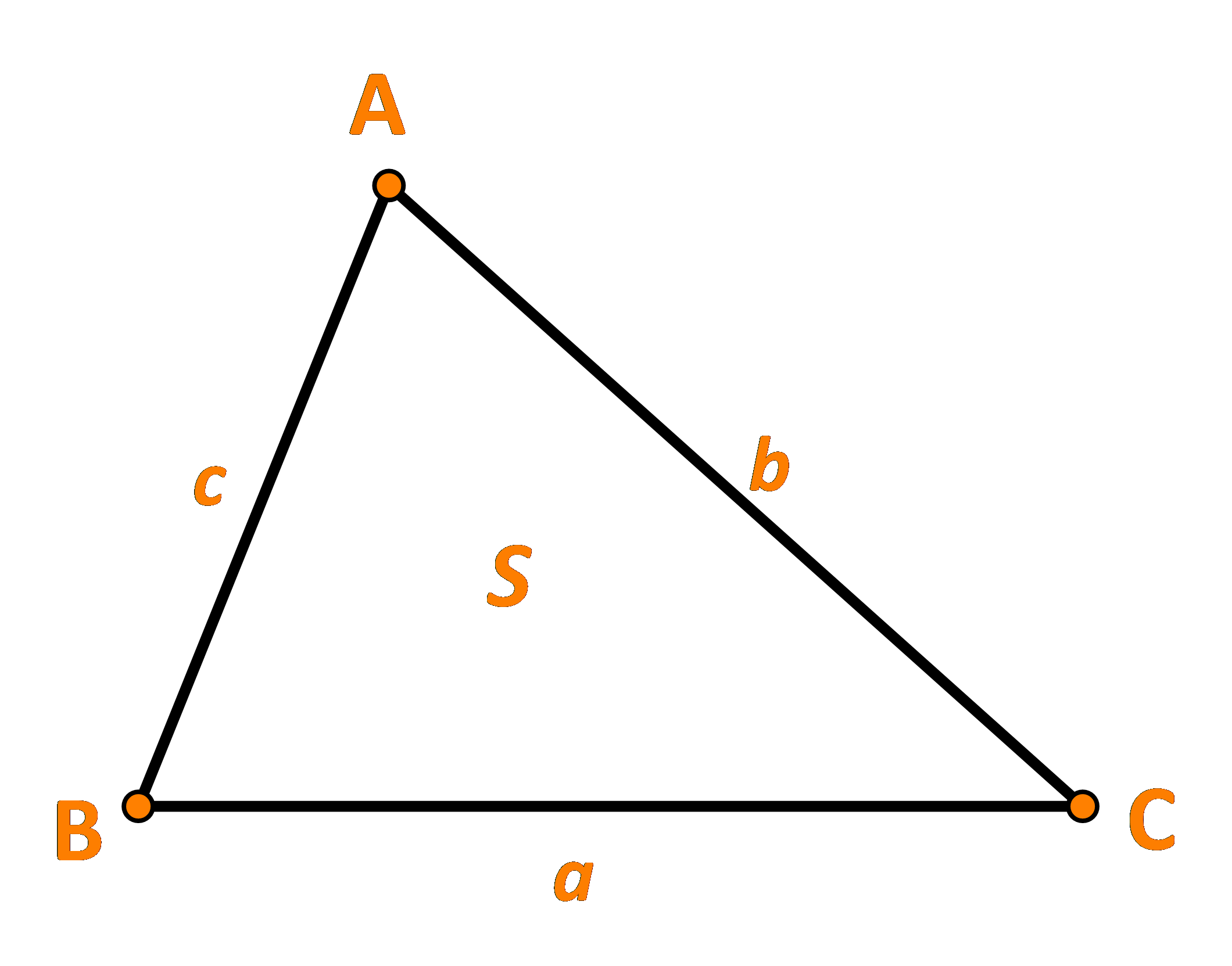
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).
a) Từ định lí cosin, chứng tỏ rằng:
\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)
b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)
Phương pháp giải:
Bước 1: Tính cos A theo a, b, c.
Bước 2: Tính sin A theo cos A.
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC ta có:
\({a^2} = {b^2} + {c^2} - 2bc.\cos A\)\( \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \(\sin A = \sqrt {1 - {{\cos }^2}A} \).
\( \Rightarrow \sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {\frac{{{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}}}{{{{(2bc)}^2}}}} \)
\( \Leftrightarrow \sin A = \frac{1}{{2bc}}\sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
Đặt \(M = \sqrt {{{(2bc)}^2} - {{({b^2} + {c^2} - {a^2})}^2}} \)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {(2bc + {b^2} + {c^2} - {a^2})(2bc - {b^2} - {c^2} + {a^2})} \\ \Leftrightarrow M = \sqrt {\left[ {{{(b + c)}^2} - {a^2}} \right].\left[ {{a^2} - {{(b - c)}^2}} \right]} \\ \Leftrightarrow M = \sqrt {(b + c - a)(b + c + a)(a - b + c)(a + b - c)} \end{array}\)
Ta có: \(a + b + c = 2p\)\( \Rightarrow \left\{ \begin{array}{l}b + c - a = 2p - 2a = 2(p - a)\\a - b + c = 2p - 2b = 2(p - b)\\a + b - c = 2p - 2c = 2(p - c)\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow M = \sqrt {2(p - a).2p.2(p - b).2(p - c)} \\ \Leftrightarrow M = 4\sqrt {(p - a).p.(p - b).(p - c)} \\ \Rightarrow \sin A = \frac{1}{{2bc}}.4\sqrt {p(p - a)(p - b)(p - c)} \\ \Leftrightarrow \sin A = \frac{2}{{bc}}.\sqrt {p(p - a)(p - b)(p - c)} \end{array}\)
b) Ta có: \(S = \frac{1}{2}bc\sin A\)
Mà \(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \)
\(\begin{array}{l} \Rightarrow S = \frac{1}{2}bc.\left( {\frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} } \right)\\ \Leftrightarrow S = \sqrt {p(p - a)(p - b)(p - c)} .\end{array}\)
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các kiến thức về vectơ, bao gồm các khái niệm cơ bản, các phép toán trên vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Bài tập này yêu cầu học sinh hiểu rõ định nghĩa vectơ, các yếu tố của vectơ (điểm gốc, điểm cuối, độ dài, hướng), và cách biểu diễn vectơ. Các em cần phân biệt được vectơ với đoạn thẳng và hiểu được ý nghĩa của vectơ trong không gian.
Bài tập này tập trung vào các phép cộng, trừ, nhân với một số thực của vectơ. Học sinh cần nắm vững các quy tắc thực hiện các phép toán này và hiểu được ý nghĩa hình học của chúng.
Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải các bài toán hình học, chẳng hạn như chứng minh hai đường thẳng song song, tìm giao điểm của hai đường thẳng, hoặc tính diện tích của một hình.
| Bài tập | Nội dung |
|---|---|
| 3.1 | Chứng minh hai vectơ cùng phương. |
| 3.2 | Tìm tọa độ trung điểm của đoạn thẳng. |
| 3.3 | Tính diện tích tam giác bằng vectơ. |
| Lưu ý: Các bài tập có thể có nhiều cách giải khác nhau. | |
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong mục II trang 73, 74, 75 SGK Toán 10 tập 1 - Cánh diều. Các lời giải được trình bày một cách logic, rõ ràng, kèm theo các hình vẽ minh họa để giúp các em dễ dàng theo dõi và hiểu bài.
Ngoài ra, chúng tôi còn cung cấp các hướng dẫn giải bài tập, các mẹo và thủ thuật để giúp các em giải quyết các bài toán khó một cách nhanh chóng và hiệu quả.
Hy vọng rằng với những lời giải chi tiết và hướng dẫn hữu ích mà chúng tôi cung cấp, các em sẽ học tốt môn Toán 10 và đạt được kết quả cao trong học tập. Chúc các em thành công!