Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục II trang 80 và 81 sách giáo khoa Toán 10 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ CD với giá của vectơ AB và PQ. Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ AB và CD có cùng hướng hay không.
Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ \(\overrightarrow {CD} \) với giá của vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {PQ} \).
Phương pháp giải:
+) Giá của vectơ là đường thẳng chứa vectơ ấy.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Giá của vectơ \(\overrightarrow {PQ} \) là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.
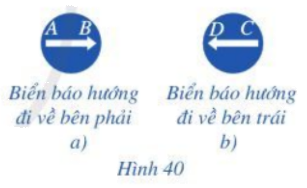
Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng hướng hay không.
Phương pháp giải:
Bước 1: Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), chỉ ra chúng cùng phương.
Bước 2: Nhận xét về hướng của hai vectơ và kết luận.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.
Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ \(\overrightarrow {CD} \) với giá của vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {PQ} \).
Phương pháp giải:
+) Giá của vectơ là đường thẳng chứa vectơ ấy.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Giá của vectơ \(\overrightarrow {PQ} \) là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.
Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng hướng hay không.

Phương pháp giải:
Bước 1: Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), chỉ ra chúng cùng phương.
Bước 2: Nhận xét về hướng của hai vectơ và kết luận.
Lời giải chi tiết:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.
Mục II trong SGK Toán 10 tập 1 - Cánh diều tập trung vào các kiến thức về vectơ, đặc biệt là các phép toán trên vectơ và ứng dụng của vectơ trong hình học. Các bài tập trang 80 và 81 thường xoay quanh việc xác định tọa độ của vectơ, thực hiện các phép cộng, trừ, nhân với một số thực, và tính độ dài của vectơ. Việc nắm vững các khái niệm và công thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài tập này yêu cầu học sinh xác định tọa độ của vectơ dựa trên tọa độ của các điểm đầu và điểm cuối. Để giải bài tập này, học sinh cần nhớ công thức:
Nếu A(xA; yA) và B(xB; yB) thì vectơ AB có tọa độ là (xB - xA; yB - yA).
Ví dụ, cho A(1; 2) và B(3; 4), ta có vectơ AB có tọa độ là (3 - 1; 4 - 2) = (2; 2).
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân với một số thực trên các vectơ đã cho. Để giải bài tập này, học sinh cần nhớ các quy tắc sau:
Ví dụ, cho a(1; 2) và b(3; 4), ta có:
Bài tập này yêu cầu học sinh tính độ dài của vectơ. Để giải bài tập này, học sinh cần nhớ công thức:
Nếu a(x; y) thì độ dài của vectơ a là ||a|| = √(x2 + y2).
Ví dụ, cho a(3; 4), ta có độ dài của vectơ a là ||a|| = √(32 + 42) = √(9 + 16) = √25 = 5.
Vectơ có rất nhiều ứng dụng trong hình học, ví dụ như:
Việc hiểu rõ về vectơ và các phép toán trên vectơ sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả hơn.
Khi giải bài tập về vectơ, học sinh cần lưu ý những điều sau:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Công thức | Mô tả |
|---|---|
| AB = (xB - xA; yB - yA) | Tọa độ của vectơ AB |
| a + b = (x1 + x2; y1 + y2) | Phép cộng vectơ |
| a - b = (x1 - x2; y1 - y2) | Phép trừ vectơ |
| k.a = (kx; ky) | Phép nhân vectơ với một số thực |
| ||a|| = √(x2 + y2) | Độ dài của vectơ a |